Roman dodecahedra between Southeast Asia and England, part 4
« previous post | next post »
Wherein we embark upon an inquisition into the divine proportions of the dodecahedron and its congeners, take a peek at the history of accounting, explore the mind of Leonardo da Vinci, and examine the humanistic physics of Werner Heisenberg*.
[*Heisenberg's father was a professor of medieval and modern Greek studies at the University of Munich in Germany. Heisenberg had more a “humanistic” education, i.e. more Latin and Greek than in natural sciences. One morning the young Werner Heisenberg discovered reading Plato's Timaeus a description of the world with regular polyhedra. Heisenberg could not understand why Plato being so rational started to use speculative ideas. But finally he was fascinated by the idea that it could be possible to describe the Universe mathematically. He could not understand why Plato used the Polyhedra as the basic units in his model, but Heisenberg considered that in order to understand the world it is necessary to understand the Physics of the atoms. (source) He contributed to atomic theory through formulating quantum mechanics in terms of matrices and in discovering the uncertainty principle, which states that a particle's position and momentum cannot both be known exactly. (Britannica | Apr 23, 2024)
—————
We have had an exciting, joyful journey through dodecahedra land, from the archeological discovery of a new specimen in England, to deep, dense discussions about the meaning and purpose of these mysterious objects, to scampering through and clambering over a playground installation of a related form. In this post, I would like to return to the essential twelveness of the dodecahedra.
I am especially sensitive to the metaphysical, mystical meanings of twelve, partly because I once had a duodenal ulcer that almost killed me. I would never have known that it had something to do with "twelve" had I not realized that its name in Chinese is shí'èrzhǐcháng kuìyáng 十二指腸潰瘍 ("twelve finger intestine ulcer"), cf. the etymology of duodenum: late Middle English, from medieval Latin, from duodeni "in twelves", its length being equivalent to the breadth of approximately twelve fingers.
In addition, my brother David (cf. Ur-David of Tarim mummy fame) is a master horoscope reader and knows his zodiac through and through. Not to mention the implications of twelve for Chinese (and many other civilizations) calendrical and astronomical sciences. Above all, for me, are the implications of the zodiac and the cycle of twelve for the history of writing, as so magisterially elaborated in the many SPPs of Brian Pellar.
Metaphysical. Did I say "metaphysical"? Yes. Now, after all the metaphysics that have come, let us delve into the physics of the dodecahedron (in the history of philosophy writ large, metaphysics comes after physics [ta meta ta physika τὰ μετὰ τὰ φυσικά]).
From the beginning of our stimulating, fruitful investigations of the Gallo-Roman dodecahedra (GRd) of the past month, we have gotten used to thinking of them as having holes on their sides and knobs at their vertices. In this episode, I will posit that those holes and knobs are artifacts of the GR phase of the evolution of the form. For the GRd are fundamentally an adaptation of what is essentially a Greek form.
Gallo-Roman culture was a consequence of the Romanization of Gauls under the rule of the Roman Empire. It was characterized by the Gaulish adoption or adaptation of Roman culture, language, morals and way of life in a uniquely Gaulish context.
GR culture was no longer pristine, pure Greek culture. Already with the Romans, it was an adaptation of the Greek, and when the Romans extended it to the provinces in the north, it was inevitably adapted even further. Things were no different with the GRd.
The Greek dodecahedron started out as one of the Five Platonic Solids.
Although, as we have seen in previous posts, one of the five Platonic Solids had more sides than the dodecahedron, namely the icosahedron with 20 faces, the dodecahedron was the epitome of all the others. As playfully expressed in X/tweet-speak:
“In the grand blueprint of the cosmos, the gods employed geometry as their divine language. The tetrahedron sparked the flames of fire, the cube laid the earth's foundation, the octahedron whispered to the winds, and the icosahedron flowed through the waters. As for the dodecahedron, the gods used it to roll the dice on the universe's fate. Such is the playful wit of celestial architects.”
If we want to know why this is so and are not advanced mathematicians and philosophers ourselves, we can do no better than read Michael Lahanas, "Plato's "Mathematical model of the Universe – Space and Time."
Plato held the view that mathematical objects "really" existed so that they are discovered by mathematicians (in the same way that new continents are discovered by explorers) rather than invented. Plato believed that mathematics provided the best training for thinking about science and philosophy. The five regular solids are named "Platonic Solids" today after Plato.
Of the 5 solids, the tetrahedron has the smallest volume for its surface area and the icosahedron the largest; they therefore show the properties of dryness and wetness respectively and so correspond to FIRE and WATER. The cube, standing firmly on its base, corresponds to the stable EARTH but the octahedron which rotates freely when held by two opposite vertices, corresponds to the mobile AIR. The dodecahedron corresponds to the UNIVERSE because the zodiac has 12 signs (the constellations of stars that the sun passes through in the course of one year) corresponding to the 12 faces of the dodecahedron.
Please reread that last sentence.
Reread it again.
Now, on to Heisenberg (1901-1976).
…But the resemblance of the modern views to those of Plato and the Pythagoreans can be carried somewhat further. The elementary particles in Plato's Timaeus are finally not substance but mathematical forms. "All things are numbers" is a sentence attributed to Pythagoras. The only mathematical forms available at that time were such geometric forms as the regular solids or the triangles which form their surface. In modern quantum theory there can be no doubt that the elementary particles will finally also be mathematical forms but of a much more complicated nature. The Greek philosophers thought of static forms and found them in the regular solids. Modern science, however, has from its beginning in the sixteenth and seventeenth centuries started from the dynamic problem. The constant element in physics since Newton is not a configuration or a geometrical form, but a dynamic law. The equation of motion holds at all times, it is in this sense eternal, whereas the geometrical forms, like the orbits, are changing. Therefore, the mathematical forms that represent the elementary particles will be solutions of some eternal law of motion for matter. This is a problem which has not yet been solved.
Heisenberg, Physics and Philosophy: The Revolution in Modern Science
Finally there is also a interesting comment by Nicholas Gier and Gail Adele:
… the most amazing vindication of Plato has come from recent surveys of the universe that indicate that the universe may indeed be a dodecahedron, whose reflecting pentagonal faces give the illusion of an infinite universe when in fact it is finite. See New Scientist (October, 2003). See www.newscientist.com/news
What do we see here?
Luca Pacioli (1445-1517), inventor of the double bookkeeping method, in a stamp shown with a dodecahedron.
Notice that, on Pacioli's desk, next to his right elbow, with not many other things, the great mathematician keeps a dodecahedron, and it is solid — no holes on its faces and no knobs at its vertices.
There are certain aspects of Pacioli's life that are very interesting and important:
Fra. Luca Bartolomeo de Pacioli (sometimes Paccioli or Paciolo; c. 1447 – 19 June 1517) was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and an early contributor to the field now known as accounting. He is referred to as the father of accounting and bookkeeping and he was the first person to publish a work on the double-entry system of book-keeping on the continent. He was also called Luca di Borgo after his birthplace, Borgo Sansepolcro, Tuscany.
Luca Pacioli was born between 1446 and 1448 in the Tuscan town of Sansepolcro where he received an abbaco* education. This was education in the vernacular (i.e., the local tongue) rather than Latin and focused on the knowledge required of merchants.
[*i.e., "abacus school", associated with Fibonacci's Book of the Abacus and his introduction of the Hindu–Arabic numeral system.]
I find that last sentence to be of extreme importance. The Phoenicians, who were also merchants and acted as middlemen throughout the Mediterranean, were responsible for the invention of the Phoenician alphabet, from which were spawned all the other alphabets of the world. This was a very vernacular thing for them to do. Similar contributions may be attributed to the Sogdians, likewise merchants across Central Asia, whom I refer to as Kulturvermittlers ("culture mediators / brokers")
Here is another portrait of Fra. Pacioli:

Portrait of Luca Pacioli (c. 1495)
(source)
The 1495 Portrait of Luca Pacioli, traditionally attributed to Jacopo de' Barbari, includes a glass rhombicuboctahedron half-filled with water, which may have been painted by Leonardo da Vinci. The first printed version of the rhombicuboctahedron was by Leonardo and appeared in Pacioli's Divina proportione (1509).
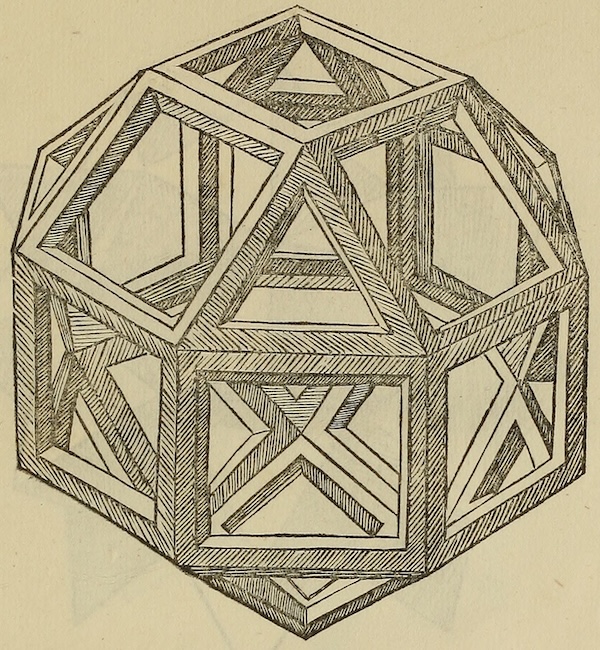
Leonardo da Vinci's illustration in Divina proportione (1509)
Why was the rhombicuboctahedron so important to men like Luca Pacioli and Leonardo da Vinci? Because it allowed for the approximation of a sphere while working from angles drawn on a flat surface.
A spherical 180° × 360° panorama can be projected onto any polyhedron; but the rhombicuboctahedron provides a good enough approximation of a sphere while being easy to build. This type of projection, called Philosphere, is possible from some panorama assembly software. It consists of two images that are printed separately and cut with scissors while leaving some flaps for assembly with glue.
("Rhombicuboctahedron" — I presume that now this cutting and gluing could be done electronically)
Although the spectacular half-filled glass rhombicuboctahedron is hanging — suspended from a thread — to Fra. Pacioli's right, there on a book next to his left hand is his beloved, trusty dodecahedron, again with no holes in its sides and no knobs at its vertices. The more I study the dodecahedra, the more I come to feel that the holes and the knobs were ultimately a function of their manufacture: to lighten their weight, decrease their cost, and to securely fix their sides together at the vertices. I believe that the original Greek dodecahedra were solid, as one would expect Platonic Solids to be. In my estimation, outstanding mathematicians and thinkers like Luca Pacioli and Leonardo da Vinci continued a tradition that went back to the Greeks.
What, then, was the purpose of keeping a solid, knobless dodecahedron, of the kind so lavishly praised by Plato? Because it constituted the geometric embodiment of the universe. It was the iconographic representation of the structure and laws of the cosmos. Put differently, perhaps one could say that the dodecahedron was the crystallization of the Platonic ideals and mathematical principles of the macrocosm.
What is meant by Platonic ideal? The Platonic ideal is the perfect, absolute, and eternal Forms. Everything in the natural world is derived from the Forms but only as an imitation or impression of those Forms. Everything is born from the Realm of the Forms and returns back there after death.(source, with an entertaining, instructive video about "Platonic Idealism in Philosophy")
I believe that Fra. Pacioli treasured his dodecahedron for the same reasons I keep these shells on my desk:
But I further believe that Plato's (and Pacioli's) comprehension of the cosmos is more profound than and superior to mine, because I can only account for the expansion and beauty of the universe, whereas the Platonists can elucidate the structure and integrity of the cosmos. To follow in the path of Plato and Pacioli, one needs a large, capacious, powerful mind — plus clarity; to adhere to the way of the snail and the nautilus, one must possess abundant inspiration and aspiration — and persistence.
Selected readings
- Roman dodecahedra between Southeast Asia and England, part 3 (5/24/24)
- "Roman dodecahedra between Southeast Asia and England, part 2" (5/12/24)
- "Roman dodecahedra between Southeast Asia and England" (4/30/24)
- "Wheat and word: astronomy and the origins of the alphabet" (3/15/24) — with references to seven substantial papers on this subject by Brian Pellar
- "The Alphabet and the Zodiac" (12/6/22)




Seth said,
June 5, 2024 @ 4:30 am
I don't think the holes could be to lighten weight and decrease cost, because of the constant pattern of different sizes. I believe those different hole sizes must be a significant part of the artifact's purpose. If the holes were just for economizing, they would be as large as possible on all sides. Also the only markings are circles around the holes, which seems to me to stress they are functional.
I'm coming back to think an idea discussed in earlier comments, that these are intended for some sort of coin-tossing game. The different hole sizes then make sense as levels of difficulty. An objection was that the sizes of coins didn't match the holes. But I'm thinking now maybe the specific way the game was played needs to be refined. The circles around a hole are the kind of flourish that can indicate "this is a target".
Then this post would be like finding a dartboard, and discussing the mathematical and mystical meaning of the circle and the wheel. "Look at this strange disc artifact which has so many circles in – there is such a history of religious significant in the structure – the Circle Of Life, the Wheel of Fortune, even the Universe returning to itself …". All true in the abstract, but the thing is a mundane game item which has the purpose of people throwing darts at it.
Victor Mair said,
June 5, 2024 @ 6:02 am
This is a long post, so I will extract these two sentences for emphasis and explanation here:
"In this episode, I will posit that those holes and knobs are artifacts of the GR phase of the evolution of the form. For the GRd are fundamentally an adaptation of what is essentially a Greek form."
I.e., the holes and the knobs of the GRd variants are adventitious to the pure Greek form.
More TK in part 5.
David Marjanović said,
June 5, 2024 @ 7:00 am
I would greatly appreciate a link to that article.
Scott P. said,
June 5, 2024 @ 8:49 am
The issue though is there is no 'pure Greek form' — we haven't found any such objects (with or without holes) in Greece. This is surprising if there were a connection, since there has been much more archaeological investigation in Greece than France.
Lucas Christopoulos said,
June 5, 2024 @ 8:55 am
"we haven't found any such objects (with or without holes) in Greece."
Idean cave of Zeus dodecahedron:
https://archiv.ub.uni-heidelberg.de/propylaeumdok/1865/1/Chanotis_Dodecahedron_2006.pdf
MattF said,
June 5, 2024 @ 9:36 am
There’s a great deal of polyhedron-related material on the Web. A good place to start is George Hart’s Encyclopedia of Polyhedrality:
http://georgehart.com/virtual-polyhedra/vp.html
Which has the nice property that the illustrations can be rotated in 3-space.
Philip Taylor said,
June 5, 2024 @ 11:53 am
The author may have meant Nature, not New Scientist, David — https://www.nature.com/nature/volumes/425/issues/6958
Victor Mair said,
June 5, 2024 @ 8:56 pm
@Philip Taylor
The article to which David Marjanović was referring is indeed in the issue of Nature whose link you supplied.
Victor Mair said,
June 5, 2024 @ 9:17 pm
The reference provided by Lucas Christopoulos is extraordinarily important because it directly links the dodecahedron to the alphabet.
Michael Vnuk said,
June 5, 2024 @ 10:36 pm
Leonardo da Vinci's illustration is a bit wonky in several places. Try following edges or shading behind other part of the structure, check widths, compare the left side with the right side, and so on. But perhaps the diagram lost some accuracy when it was converted to an engraving for printing.
Philip Taylor said,
June 6, 2024 @ 3:58 am
Thank you for that confirmation, Victor. David, there are in fact two articles in that issue of Nature which are relevant — the first, the one entitled "The shape of the Universe" and blazoned on the front cover, is by George F. R. Ellis and commences :
while the article to which that article refers is entitled "Dodecahedral space topology as an explanation for weak wide-angle
temperature correlations in the cosmic microwave background", is by Jean-Pierre Luminet, Jeffrey R. Weeks, Alain Riazuelo,
Roland Lehoucq & Jean-Philippe Uzan and commences
Brian said,
June 6, 2024 @ 8:19 pm
I really enjoyed reading this post — very informative and thought provoking. In particular, there is comment that Professor Mair makes regarding the manufacture of the dodecahedra:
“The more I study the dodecahedra, the more I come to feel that the holes and the knobs were ultimately a function of their manufacture: to lighten their weight, decrease their cost, and to securely fix their sides together at the vertices. I believe that the original Greek dodecahedra were solid, as one would expect Platonic Solids to be.”
After reading this, it suddenly struck me that if the dodecahedra were indeed symbolic of the shape of the cosmos and the 12 houses of the zodiac, then what might amount to a more accurate representation of its shape would be a hollow dodecahedron. That is, the word “solid” in “The Platonic Solids” can be a red herring, for though the four-sided cube is associated with solid matter (earth), the octahedron is associated with atmosphere (air) — which we all reside in and under. In a similar way to the eight-sided octahedron, the twelve-sided dodecahedron was construed to represent the outer shape to the mostly empty space that the 12 constellations of the zodiac, the planets, and the earth inhabit “within.” This idea of mostly empty space within a dodecahedron might be why the Roman dodecahedra were deliberately fashioned as hollow. As I mentioned previously, the varying size holes could then account for the varying amounts of light that the sun provides during the 12 months of the year (per its 12 sides, which, as mentioned earlier, via Plato, are symbolic of the 12 constellations of the zodiac that the sun journeys through — and which face “within” towards its center).
And where does that light come from? To speculate a bit more, and to try to think outside the box (pun intended), the origin of the light might be derived from the Greek notion of the “Monad”, “The One,” the “unseen” deity who presides “above” everything — i.e., just above the open/holed surface of the material twelve-sided dodecahedron (the blueprint of the cosmos/everything). That is, the Monad resides at the highest level of what the Greeks and Gnostics call the super celestial sphere, the “pleroma,” (the region of light constituting the “fullness of the Godhead” and the realm of all of the Aeons — the pairs of male/female gods). This pleroma would, thus, constitute the mathematically modeled surface of the dodecahedron itself. As the ultimate source of the light of the pleroma, the “unseen” Monad would then seem to correlate to the varying size holes in the surface of the Roman dodecahedra (from which the varied light it creates enters) and/or to the unseen region that that surface is encased in (which then enters those holes in the surface).
But it’s the mathematical aspect of the Monad and its Aeons that just might help to understand the formation of the 20 points or outer “knobs” that rise above, or “outside,” the 30 lines of the surface/super celestial sphere of the Roman dodecahedra.
But before I discuss the knobs and the correlation of numbers, it’s important to note that the idea of a Monad comes out of Greek Philosophy (via Pythagoras, who was said to have travelled to and studied in Egypt), where
“the Monad is the Supreme Being, divinity or the totality of all things . . . According to Hippolytus, the worldview was inspired by the Pythagoreans, who called the first thing that came into existence the "monad", which begat (bore) the dyad (from the Greek word for two), which begat the numbers, which begat the point, begetting lines or finiteness, etc.” [Wiki]
It should also be noted that Pythagoras, who influenced Plato, is also credited with the invention of the Five Regular Solids, which includes the Dodecahedron. This idea of the Monad then went on to influence the later Christian Gnostics. According to the Gnostic text Apocryphon of John (c. 180):
“The Monad is a monarchy with nothing above it. It is he who exists as God and Father of everything, the invisible One who is above everything, who exists as incorruption, which is in the pure light into which no eye can look.” [Wiki]
Also,
“In many Gnostic systems, God is known as the Monad, the One. God is the high source of the pleroma, the region of light. The various emanations of God are called æons.” [Wiki]
But more importantly, the Gnostic systems appear to follow the mathematics of the Pythagoreans and the Five Solids. According to Marcus, the Gnostic Aeons are “numbers and sounds.” [Wiki]. That is, from the Monad, the “one,” came the Aeons — the dyads, the “two” (male and female pairings of the gods/goddesses, the “sygygies”) of the Ogdoad, the “eight” (which some believe might have its roots in the eight pairs of gods of the Egyptian Ogdoad) [Wiki], of the “fifteen” pairs of 30 male/female divine beings in some of the systems, such as Valentinus’. Thus, there is a 1, 2, 8, 15, 30 sequence of the formation of the Gnostic gods.
This unfolding mathematical sequence of the Gnostic system appears to approximate the unfolding sequence of the Greek “Monad” and the Five Platonic Solids: that is, the Greek solids “came into existence” via the “monad,” the “one,” which then “begat” the “dyad” (two), which then “begat the numbers,” which then “begat the point,” which then begat the “lines.” In the dodecahedron, those lines are 30. Thus, it’s interesting that the unfolding of the “Monad” and numbers that make up the 30 Gnostic Aeons (who are “numbers and sounds”) appear to correlate to the unfolding of the “Monad” and numbers that result in the 30 lines of the dodecahedron (which is fitting, as the 30 Aeons are the Ogdoad, the gods, and thus, would seem to naturally fit as the 30 lines of the one Platonic Solid that is the blueprint or structural model of the cosmos).
Furthermore, this unfolding of the “one” into “two” into “thirty” might then help explain why there are the 20 knobs on the “outside” of the Roman dodecahedra. That is, they appear to symbolize the “points” of the 20 vertices that unfold into the 30 lines that compose its form. Those points have zero dimension and are thus symbolic of “the invisible One who is above everything, who exists as incorruption, which is in the pure light into which no eye can look” (akin to the center point of god as a circle, whose center is everywhere and circumference nowhere). This could further help explain why those points/knobs are not seen on a normal dodecahedron. They are there for symbolic purposes in the same way that the varying size holes of the surface symbolize the varying amounts of light that shine in from the pleroma and Monad.
Lastly, it’s important to re-emphasize Professor Mair’s point about the Greek rock crystal dodecahedron found in a Greek Idaean cave. Though it’s hard to correlate the letters with the constellations of the zodiac [as the Greek numbering system used the letters as numbers, and, thus, the letters could simply be artifacts of the numbers used for the dice. Further, the fact that the sequence of numbers do not go to 12, and the fact that the numbers are separated from each other, further distances those numbers from a logical correlation to the zodiac and the alphazodiac], the strong possibility that it was used for divination/ritualistic purposes is critical, for that helps to establish a sequence of its religious use from Greece to Rome to the Roman territories. The fact that others have also been found in ritualistic or ritualistic-like settings also lends weight to this (i.e., the crystal dodecahedron dice found in a Roman grave in Patrae that appears to be strongly correlated to “divinatory activities”; the Roman dodecahedron use for “divination games” that was found at the Cathedral of St. Pierre with the Latin inscriptions of the 12 houses of the zodiac; the Roman dodecahedron found in a pit on a hilltop; or the Roman dodecahedra found within caches of money, as though they were used as a good luck charm, etc.).
Lucas Christopoulos said,
June 7, 2024 @ 1:49 am
@Brian
When you said the "Platonic Monad," (and the Demiourgos δημιουργός; architect of the Universe), and the "Invisible Sun," I immediately thought about Neo-Platonists and their "Three Suns," not the Gnostics.
Their influence in Geometry and building structure can also be found in Islamic arts.
Neoplatonism and Geometry in Islamic Art:
https://academic.oup.com/arthistory/article-abstract/21/1/135/7278429?redirectedFrom=PDF
Benjamin E. Orsatti said,
June 7, 2024 @ 7:46 am
Why do physicists want the universe to be finite so badly? (see, e.g., Carlo Rovelli). It's all "Occam's Razor", until it comes to the topology of the universe (which the math seems to suggest is Euclidean, flat (unconnected), and infinite), and then, all of a sudden, they're all, "uh, maybe it's a dodecahedron?".
Michael Vnuk said,
June 7, 2024 @ 10:14 pm
I wondered what was the point of the rhombicuboctahedron. On the face of it, not much, I thought. It’s just a shape. But then I counted the faces: 26.
Now, not only is 26 the approximate number of weeks between the two solstices of a year (or, even more remarkably, between the two equinoxes), and the exact number of red cards in a pack of cards (or black ones, if the colour suits you better), it is also the number of letters in the alphabet. This is deeply significant.
Similarly, the number of points on a rhombicuboctahedron is 24, which, besides being twice the number of zodiac signs, is the exact number of letters in the Greek alphabet. And the number of edges on a rhombicuboctahedron is 48, the number of upper and lower case letters in the Greek alphabet. That’s more significant relationships.
All this explains why the rhombicuboctahedron was included in paintings, and why it is shown larger than the dodecahedron. It was to stress the importance of language and writing – more important than geometry and the rest of mathematics. English (and other languages that use the 26 letters) and Greek are the best languages, because their alphabets are encapsulated in the rhombicuboctahedron.
Hang on, you might say, the alphabet hasn’t always had 26 letters, and the Greek alphabet hasn’t always been 24 letters. It’s true, but don’t you think that someone like Leonardo da Vinci, acknowledged by many as a really smart cookie, couldn’t have had a deeper insight into how the alphabets would finally evolve into their perfect forms.
Another interesting feature of the rhombicuboctahedron is the number of triangular and square faces, 8 and 18 respectively. If you take an equilateral triangle positioned point down, and then remove the top edge, it is a V. If you take a square and remove its right edge, you have a good approximation to a C. Those letters, V and C, obviously stand for ‘vowel’ and ‘consonant’. Therefore, the alphabet contains 8 vowels and 18 consonants. The 8 vowels are A, E, I, O, R, U, W and Y. Besides A, E, I, O and U, most references will say that Y can be a vowel, but the rhombicuboctahedron confirms that Y is a vowel, and the same goes for R and W, which some more enlightened researchers have considered to be vowels.
There’s much more that can found in the rhombicuboctahedron. I have discovered a truly marvelous proof, but this comment box is too small to contain it.
Lucas Christopoulos said,
June 7, 2024 @ 10:41 pm
divination with dodecahedron
https://www.youtube.com/watch?v=Jknrt4PpEAY
Diane Conte said,
June 25, 2024 @ 9:48 am
It is the top of a Roman Camp tent. Poles are different sizes, rope was used to secure to the pegs to the poles and allowed wall hight and configuration to be adjusted.