Bembé, Attis, Orpheus
« previous post | next post »
A couple of years ago, I wrote about the off-beat placement of song syllables (and other other notes) in popular music of the past century. This can be seen as the displacement of events from an underlyingly regular meter, but often it can also be seen as a basic metrical pattern in which events don't fall at evenly-spaced time intervals ("Rock syncopation: stress shifts or polyrhythms?", 11/26/2007). The example that I looked at was a maximally simple one — the 3+3+2=4+4 "habanera" rhythm that rocked America in the late 19th century.
Today's post is about some rhythms that arrange events in a recurring cycle of 12 time-units. And although I'll start with another Afro-Cuban pattern, the Bembé, today's analysis will look at connections in renaissance Italy and ancient Rome, rather than in 20th-century America. (Attention conservation notice: unless you're interested in geeking out on a detailed analysis of metrical patterns, you'll probably want to skip onwards to some of our other fine posts…)
Godfried Toussaint starts his 2003 paper "Classification and Phylogenetic Analysis of African Ternary Rhythm Timelines" this way:
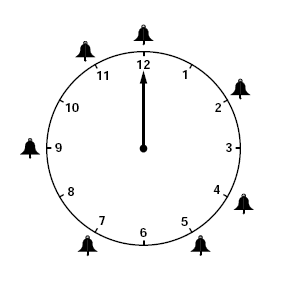
Consider the clock [below], and assume the clock runs so fast that it makes a full revolution in about two seconds. Now set the clock ticking starting on the hours of twelve, two, four, five, seven, nine, and eleven, for a total of seven strikes per clock cycle, with the first strike of the cycle at twelve. […]
The resulting pattern rings out the predominant African rhythm time-line that has travelled to America and beyond, and has become the most well known of all the (12/8)-time bell patterns. It is known internationally mostly by its Cuban name, the Bembé, a name given to a feast celebrated with drums to entertain the orishas. In the following, simple mathematical arguments will be given that may explain why the Bembé has taken center stage among the 12/8 time bell patterns.
In a flat, metronomic rendition, the Bembé pattern sounds like this:
Toussaint notes that there are several different ways of putting this pattern into conventional musical notation:
The third row [below] shows that although the Bembé is a ternary rhythm normally notated in 6/8 or 12/8 meter, some authors describe it in 4/4 time with triplets. The fourth row depicts the rhythm with the smallest convenient notes and rests. The final row shows the Bembé in the Box Notation Method developed by Philip Harland at [UCLA] in 1962. If we connect the tail to the head of this last diagram and draw it in the form of a circle in clockwise direction with the head at 12 o'clock, we obtain the clock representation […], where the squares […] filled with black dots correspond to the positions of the bells […].
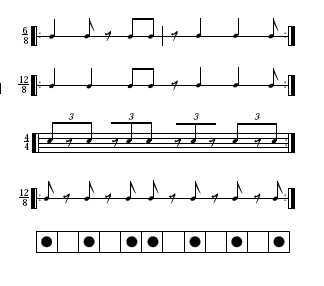
The box notation method is convenient for simple-to-notate rhythms like bell patterns […]. A commonly used convenient variant of box notation used in text documents is simple to use the letter "x" to denote the strike fo the bell or note onset, and the period symbol "," to denote interval units between the note onsets. For example, the Bembé pattern […] then become [x.x.xx.x.x.x].
You could also represent such patterns in terms of a sequence of note (or inter-onset) durations, represented as small-integer multiples of the minimal time unit, so that the Bembé pattern becomes 2+2+1+2+2+2+1.
A syncopation-as-displacement analysis of the Bembé pattern might start with six quarter-notes in 12/8 time, with the third quarter-note subdivided into two eighth notes, and the last three quarter notes (in blue) each displaced to the right by one eighth-note (to the positions in red):
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| x | x | x | x | x | x | x | |||||
| x | x | x | x | → | x | → | x | → | x |
A clue that such patterns might not be just a surface stylistic shifting of a deeper "square" or divisive rhythm was suggested by Jeff Pressing (“Cognitive Isomorphisms between Pitch and Rhythm in World Musics: West Africa, the Balkans and Western Tonality,” Studies in Music 17: 38–61, 1983). He observed that the Bembé rhythm is curiously isomorphic to the (major) diatonic scale. Thus the sequence of inter-onset time-unit differences of the seven Bembé time-points 0-2-4-5-7-9-11 is 2-2-1-2-2-2-1, just as the sequence of pitch intervals in semi-tones separating the major-scale tones C-D-E-F-G-A-B-C is 2-2-1-2-2-2-1:
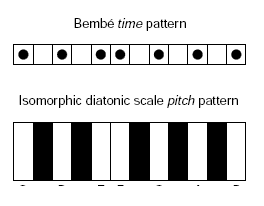
Or compare the "circle of fifths" in pitch classes, whose first seven steps generate all and only the diatonic scale-steps F-C-G-D-A-E-B, with the relative time-locations generated by successively adding 5 to 11, mod 12. Thus the expression in R (11+(0:6)*5)%%12 yields 11 4 9 2 7 0 5, which after sorting are the Bembé locations 0-2-4-5-7-9-11.
Toussaint also generalizes Simha Arom's notion of "rhythmic oddity" by counting the number of "bi-partitions": pairs of onsets that partition the entire interval into two subintervals of equal length. "The fewer equal bi-partitions a rhythm admits, the more rhythmic oddity it possesses." It's obvious that any way of placing 7 notes in a 12-unit rhythmic cycle must admit at least one bi-partition — for a hint in the direction of a proof, think of placing the notes on the numbers of clock face. The Bembé pattern achieves this maximum of rhythmic oddity — and any other pattern that does so must be a variant form of it.
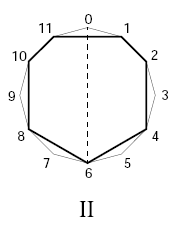
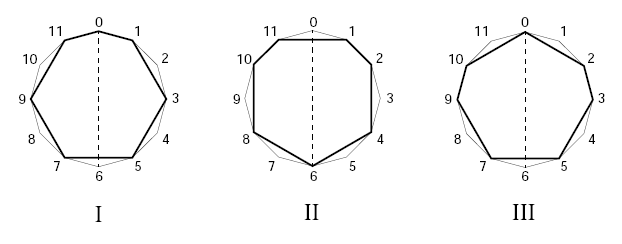
Toussaint proposes to generate the observed set of seven-out-of-twelve rhythms in traditions around the world as rotations of three basic "necklace" patterns:
Pattern III underlies the Bembé rhythm and the major scale; six of its seven rotations (starting each of its seven notes) generate attested patterns known by various names in various world-music traditions. Pattern II, which allows two bi-partitions, generates three attested rhythmic patterns, and corresponds to the (ascending melodic) minor scale; Pattern I, which allows three bi-partitions, generate two attested rhythmic patterns, and corresponds to a whole-tone-plus-one scale.
For some other interesting mathematical properties of various ways of arranging 7 or 5 notes in length-12 cycles, see Toussaint's paper. The relevant point here is that these rhythms need not be explained as derived by superficial time-shifting of events in divisively regular "deep structures", as David Temperley has suggested ("Syncopation in Rock", Popular Music 18(1), 1999 — see my earlier post for discussion). Rather, they can plausibly be seen as cyclic patterns whose projections onto a circle are not derived from regular polygons at any level of analysis, but are generated by other principles.
Next I'd like to look at a case where the traditional analysis, going back to classical times, is analogous to Temperley's analysis of rock syncopation. I'll argue that the traditional analysis is probably wrong or at least incomplete, and that an analysis like Toussaint's seems more promising.
 Of the 116 extant poems of Catullus, one (#63 in the standard enumeration) is a mini-epic telling the story of Attis. He was the mythical consort (and/or son) of Cybele, whose cult was imported from Phrygia to Rome in 204 B.C., based on a prophecy that this would help defeat Hannibal. The meter of Catullus 63 is galliambic, which the OED calls the "Epithet of a lyric metre (founded on the Ionic a minore tetrameter catalectic, with anaclasis), supposed to have been used by the priests of the Phrygian Cybele in their songs".
Of the 116 extant poems of Catullus, one (#63 in the standard enumeration) is a mini-epic telling the story of Attis. He was the mythical consort (and/or son) of Cybele, whose cult was imported from Phrygia to Rome in 204 B.C., based on a prophecy that this would help defeat Hannibal. The meter of Catullus 63 is galliambic, which the OED calls the "Epithet of a lyric metre (founded on the Ionic a minore tetrameter catalectic, with anaclasis), supposed to have been used by the priests of the Phrygian Cybele in their songs".
The etymology is [f. L. galliamb-us a song of the Galli or priests of Cybele] (And apparently the Galli were so named due to some imagined connection with Gaul.)
The theory of syncopation is implicit in the description "ionic a minore tetrameter catalectic with anaclasis".
According to the OED, ionic is (sense 4) the "name of a foot consisting of two long syllables followed by two short (‘ionic a majore’), or two short followed by two long (‘ionic a minore’)". Catalectic means "Of a verse: Incomplete in its syllables; wanting a syllable in the last foot. Often in postposition in imitation of Latin." And anaclasis means "In Ionic verse: an interchange of the final long syllable of the first metron with the opening short syllable of the second." In a duration-sequence notation, that would be
[1122 1122] → [1121 2122]
Or in a tabular form of the box notation, again showing the effect of anaclasis on two adjacent ionics:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| x | x | x | x | x | x | x | x | ||||
| x | x | x | x | x | ← | x | x | x |
In other words, "anaclasis" is really equivalent to syncopation, i.e. a shift of a "note" from position 6 to position 5 in a 12-unit rhythmic cell corresponding to two ionic feet.
Adding the second pair of ionic feet (another twelve time units; and the catalexis (i.e. omission of the last syllable); and the fact that the last syllable is "common" (i.e. either a long or a short-plus-rest will fit); and the (stylistically standard) resolution of the last long syllable; we get:
| 1. | 1122 1122 1122 1122 | ionic a minore tetrameter |
| 2. | 1122 1122 1122 112(2) | catalectic |
| 3. | 1121 2122 1121 212(2) | with anaclasis |
| 4. | 1121 2122 1121 21x(2) | (last syllable is "common") |
| 5. | 1121 2122 1121 111x(2) | (with the usual resolution) |
According to this discussion, about 2/3 of the poem's 93 verses have exactly the pattern shown in 5, for instance
10 quătĭēnsquĕ tērgă taūrī tĕnĕrīs căuă dĭgĭtīs
"and beating the hollow oxhide with delicate fingers"
The other lines mostly differ in terms of where "resolution" (the substitution of two shorts for a long or vice versa) takes place — a scanned version of the whole poem is here.
If we treat the shorts and longs of the basic galliambic meter as a literal metering of time, a metronomically exact version of the pattern sounds like this:
And musically-trained readers will have noticed that the anaclasis can also be seen as creating a hemiola pattern, in which two ternary groups — here (1+2)+(1+2) — substitute for three binary groups — here 2+(1+1)+2. Hemiola is usually seen as exploiting the ambiguity of two alternative regular subdivisions of 6 time-units. But in this case, the substitution occurs in the middle of the 12-time-unit ionic dimeter, and the resulting first half-line is a new regular pattern 1+1+2+1+2+1+2+2, in which the "beat" is most naturally heard (I think) as 1+1+2+1+2+1+2+2, i.e. falling on the 3rd, 6th, and 9th time-units.
This is can be seen as subdividing 12 into 2+3+3+2+2 (and the second half-line follows the same beat locations, differing only in subdividing an additional 2-item position, and omitting the last one). This basic 2+3+3+2+2 division of 12 time-units is reminiscent of the habanera's 3+3+2 division of 8 time-units.
And if we "unresolve" the initial duple 1+1, then the result of applying anaclasis to two ionic a minore feet is 2+2+1+2+1+2+2, which is the version of Toussaint's "necklace" pattern II that starts at 6 o'clock:
Again, it's plausible to think of this as a rhythmic structure with its own internal logic, rather than a pattern derived by superficial event-shifting from a deeper sequence of all-equal binary time divisions.
In Monteverdi's Orfeo, at the end of the celebration of the wedding of Orpheus and Euridice, the hero sings an aria that begins:
Vi ricorda o boschi ombrosi,
de' miei lunghi aspri tormenti,
quando i sassi a' miei lamenti
rispondean fatti pietosi?
Shady grove, do you remember
my long bitter agonies
when my howls made the rocks
pity me in response?
The score for the first couplet looks like this:
(from p. 26 of the version here).
If we represent each metrically-relevant syllable by an integer (here always 1 or 2) representing the number of 8th-note positions it occupies, the numerological scansion for these seven lines is:
| vi ricorda o boschi ombrosi, | 11212122 |
| vi ricorda o boschi ombrosi, | 11212122 |
| de' miei lunghi aspri tormenti, | 11221122 |
| quando i sassi a' miei lamenti | 11211222 |
| rispondean fatti pietosi? | 11212122 |
| vi ricorda o boschi ombrosi, | 11212122 |
| vi ricorda o boschi ombrosi, | 11212122 |
A metronomically-clapped copy of these sequences sounds like this:
Musically, this aria exhibits a regular alternation between half-bars of 2+2+2 and 3+3 — and you should be able to hear, as well as see, the similarity of this rhythm to the galliambic. And again, it's plausible that this regular hemiola pattern should be seen as an underlying rhythm on its own terms, not as a sequence derived by superficial event-shifting from a deeper pattern that is uniformly 2+2+2 or uniformly 3+3.
(The galliambic-like meter of Vi Ricorda may not be an accident, given the historical analogies between Attis and Orpheus. Monteverdi may have been conscious of the connection; and it's also possible that some Italian folk traditions preserved metrical forms associated with the Cybele cult. And note that Monteverdi's original 1607 version of Orfeo ended with the hero torn to pieces by Thracian Maenads, as in Ovid's version of the story. On the other hand, regular patterns of hemiola were pretty common in European music of the time.)
A version of this aria sung by Philippe Huttenlochner is available on YouTube ("Vi ricorda" start at about 0:42):

Noetica said,
May 9, 2009 @ 9:30 am
Fascinating, Mark. I intend to study this closely. Just some quick observations for now.
I was sad to see from one of your links that Jeff Pressing died in 2002, aged only 55. I remember him from La Trobe University in Melbourne. He used to whistle subjects and countersubjects from Bach fugues as he shopped in the supermarket!
On the traditional notations in your quote from Toussaint, the first line in 6/8 and the second in 12/8 use notes of strangely arbitrary duration. There is no reason, for example, to make the second note in the 6/8 a quarter note, but the corresponding note in the 12/8 an eighth note followed by a rest. Indeed, there is good reason to represent all of the notes in the 6/8 and 12/8 examples as eighth notes followed by a sufficient of rests, as is done in the fourth line. After all, only the onsets are of interest. (I make these points because some readers might think they are missing some distinction marked by those variant durations, where no relevant distinction is being made.)
Anyone wanting elementary background for the notion of the diatonic applied to rhythms might look at the article Diatonic and chromatic at Wikipedia, especially this section.
rootlesscosmo said,
May 9, 2009 @ 10:33 am
The Cuban rhythm I learned from musician friends is the clave, a sequence of sixteen beats in which one, four, seven, eleven, and thirteen are accented.
[(myl) OK, we're getting there — 8 was in 2007, 12 is today, 16 is maybe next year. Meanwhile, see GT Toussaint, "A mathematical analysis of African, Brazilian, and Cuban clave rhythms", and "The Geometry of Musical Rhythm".]
Dmitri said,
May 9, 2009 @ 10:46 am
Hi Mark,
Well done! An instant blogosphere classic … I never realized that "Vi ricorda" was a disguised version of the melodic minor scale, that's very cool. A few comments.
1. I didn't follow this: "The Bembé pattern achieves this maximum of rhythmic oddity — and any other pattern that does so must be a variant form of it." What about 0123456, which also has only one "bipartition" 06? (It's actually the rhythm you get when you multiply the diatonic rhythm by 5.) I think I'm missing something here.
[(myl) Well, mod(5*(1+[0 2 4 5 7 9 11]),12) → [ 5 3 1 6 4 2 0] is sort of "a variant form", right? But okay, let's say that any single-bipartition pattern whose elements are reasonably well spaced out will be a simple transformation of Bembé.]
2. With respect to "they can plausibly be seen as cyclic patterns whose projections onto a circle are not derived from regular polygons at any level of analysis, but are generated by other principles." Many people think it's relevant that the Bembé rhythm is the best approximation to a regular 7-gon available in a discrete 12-unit circle. Hence, there could be a "regular polygon" lurking here.
[(myl) Fair enough. My main point, though, is that it's not (always) helpful to think of such rhythms as underlyingly 3/4 or 4/4 or whatever, with a few of the notes superficially shifted for stylistic reasons.]
3. There's a pitch analogue to the hemiola-quality of the "Vi ricorda" rhythm. The ascending melodic minor scale (also known as the "acoustic" scale), can be seen as a hybrid of the 2+1 "octatonic" and the 2+2 "whole tone." Many composers — notably Debussy — use the scale to mediate between these different tonal worlds. This is a pitch analogue to using the "Vi ricorda" rhythm to mediate between duple and 2+1 ternary passages.
Kenny V said,
May 9, 2009 @ 11:35 am
I see connections here to the other Aeolic meters, notably the hendecasyllabics of Catullus, though also in Alcaeus and Sappho.
Also reminiscent of the clapping beat that begins The Game's This Is How We Do.
Dmitri said,
May 9, 2009 @ 1:41 pm
"But okay, let's say that any single-bipartition pattern whose elements are reasonably well spaced out will be a simple transformation of Bembé."
I'm not even sure that's exactly true. You can get a single-bipartition pattern by choosing one element from each of the six pairs {0, 6}, {1, 7}, {2, 8}, {3, 9}, {4, 10}, {5, 11}, and then adding any additional note. This leaves a pretty wide range of choices: something like 0, 1, 3, 4, 5, 8, 10 is quite well spaced-out but not a simple transform of Bembé.
What is true is that any sufficiently well spaced-out seven-note pattern will be a simple transform of Bembé — which is a stronger statement, since it doesn't make reference to bipartition. And it's also true that the next-most even patterns have multiple bipartitions.
Actually one interesting rhythm, which Godfried doesn't consider, is 0134689, the third most-even seven-note rhythm, which incorporates both the ternary and quadruple divisions of the measure (048 and 0369). (I suspect Godfried is focusing on rhythms that can be formed with just two beat lengths.)
Anyhow, there's tons of reasons why the Bembé pattern is interesting, so your larger point is valid. Again, great post!
Mark Liberman said,
May 9, 2009 @ 3:04 pm
@Dmitri: Hmm. You're right, of course.
Here's another way to come at it, which I think expresses what I would have meant to say if I'd thought about it first.
The only way to add up seven intervals of 2 and 1 to make 12 is to use five 2s and two 1s.
We place one of the 1s first (which we can do without loss of generality, since we'll treat circular permutations of the array as members of the same family).
Then there are six places to put the other 1:
(1) 1122222
(2) 1212222
(3) 1221222
(4) 1222122
(5) 1222212
(6) 1222221
But (6) is a circular permutation of (1), (5) is a circular permutation of (2), and (4) is a circular permutation of (3). So there are only three possible families, or "wheels" as Toussaint calls them, which are based on his "necklaces" I, II, and III.
Of those, all the single-bipartition patterns are rotations of (3), i.e. members of the Bembé wheel.
If we allow one or more longer segments into the mix, then of course things change.
Tom Recht said,
May 9, 2009 @ 3:06 pm
Mark, the isomorphisms between rhythmic patterns and Western scales are interesting, but I'm not sure if there's supposed to be a deeper point (since the Pressing paper you cite doesn't seem to be online). Is this claimed to be more than an accidental consequence of the fact that there are only so many "ways of arranging 7 or 5 notes in length-12 cycles""?
scratchdaddy said,
May 9, 2009 @ 3:15 pm
"And apparently the Galli were so named due to some imagined connection with Gaul."
I wonder if the Galli might refer to the inhabitants of Galatia in central Anatolia, which was settled by a group of Gauls who stormed through Greece in, I think, the 6th century B.C.? I believe Phrygia was a neighboring kingdom.
Mark Liberman said,
May 9, 2009 @ 3:24 pm
Tom Recht: Is this claimed to be more than an accidental consequence of the fact that there are only so many "ways of arranging 7 or 5 notes in length-12 cycles""
It's certainly a consequence of the combinatorics involved, and Pressing (along with many before and since) argues (I think convincingly) that in both cases the consequences are aesthetically consequential. Whether the analogies (and their limits) are "accidental" is a question that's above my pay grade.
My point in citing the analogy is mainly to argue for the plausibility of the view that apparently "syncopated" rhythms sometimes have an inner logic other than as a superficial displacement of events in a rhythmic pattern whose deep structure is evenly divisive. We don't generally insist that the diatonic scale is just a superficial distortion of an underlying whole-tone scale, for example (says he, glancing nervously over his shoulder at Dmitri).
Tom Recht said,
May 9, 2009 @ 4:03 pm
"The consequences are aesthetically consequential" – fair enough. I think I took you to be saying that people have made the case that similar patterns in these two domains are somehow related, e.g. by being aesthetically consequential in similar ways.
I don't find the analogy with scales very convincing as an anti-displacement argument, though. An octave contains a mathematically important internal landmark – the fifth – which is not centrally placed, and not part of the whole-tone scale, so it would be unsatisfying to posit the whole-tone scale as an 'underlying form'. Nothing like this applies to rhythmic patterns, though, as far as I can see.
Sili said,
May 9, 2009 @ 4:43 pm
Nothing wrong with geeking out. Ben Goldacre must approve.
(Yes, I skipped straight to the end. I don't 'get' music. :goes back to listen to Mendelsohn Weekend on Radio3:)
JeffE said,
May 9, 2009 @ 4:58 pm
Godfried will love this!
Dmitri said,
May 9, 2009 @ 7:33 pm
Tom,
I think there are some non-accidental analogies between pitch and rhythm that are actually quite revealing — though the subject is very delicate since of course there are also important disanalogies too!
One important similarity concerns the property of being "nearly even but not exactly so." It's relatively intuitive that a repeating rhythm shouldn't be completely even (because that's boring), but also not very uneven (because that doesn't reinforce a sense of pulse). To see this, try clapping on beats 0, 4, and 8 (out of 12) and then 0, 1, and 2 (out of 12). Neither pattern really makes you want to get out of your seat and dance.
On the other hand, nearly-but-not-quite even rhythms often suggest a pulse while also being interesting. Lots of popular rhythms (as Godfried and Jeff Pressing point out) have this property.
Now it turns out that near-but-not-quite evenness is an important property in the pitch domain too: it's (non-accidentally) connected to acoustic consonance (major triads, dominant seventh chords, diatonic scales all divide the octave nearly but not exactly evenly) and it's crucial to the unification of harmony and counterpoint that is central to many Western styles.
Because of this sort of thing you find similar patterns in both domains … the "Vi ricorda" example Mark gives is a case in point — the rhythmic structure does have an analogue in the scalar procedures of 20th-century composers. Unfortunately, a longer explanation doesn't fit in the margins of this comment box. ;-)
Coby Lubliner said,
May 9, 2009 @ 8:15 pm
Though I've listened to quite a bit of Cuban music in my life, I've listened to Balkan music more, and I tend to hear a 2+1 as a 3, so that the Bembé rhythm sounds to me not like 2+2+1+2+2+2+1 but 2+3+2+2+3 (i.e. five beats). This happens to be the rhythm of the Macedonian dance called Beranče.
Noetica said,
May 9, 2009 @ 10:15 pm
Right. And the first thing we notice about the whole-tone scale is its surfeit of symmetry – its dividing the octave too uniformly to ground harmonic and melodic structure. (And it's no longer an octave when the whole-tone scale divides it, but a septave!) We find something similar in the ambiguity of the augmented triad (itself implying a whole-tone scale), which does divide the octave evenly, like the arguably "rootless" diminished seventh chord. And each of these two chords, at least when presented out of context, is aurally indistinguishable from its own inversions.
The whole-tone scale is therefore not a suitable theoretical foundation from which to derive more commonly used scales, any more than major and minor triads are considered variations on the augmented triad, for all its fearful symmetry.
Mark, you interpolate this note above:
First, isn't there technically a conflation of metre and rhythm here? 3/4 and 4/4 are metres, and do not consist of notes as rhythms might be said to consist of notes; so these rhythms could hardly "be" underlyingly 3/4 or 4/4, with "some notes shifted".
Second, it is interesting that you mention 3/4 here. This was not among the metres discussed at the outset. We had Toussaint's examples of Bembé represented in (2x)6/8, 12/8, and 4/4 with triplets. But in fact, as Pressing, Toussaint, and others point out, the underlying metres that accommodate the pattern, construed as eighth notes and eighth-note rests, include 3/2 and 6/4 or (2x)3/4. In fact Bembé fits far more comfortably with these metres, to my ears, than with those Toussaint gives in his sample representations. At least I find it easier to clap Bembé eighth notes against 3/2 or 6/4. Don't we all?
It is dangerously easy to import European baggage, as several of the writers in this area point out. When we think of 12/8, if we are trained in traditional European ways we automatically think of a division into four major beats, each subdivided into three. But for this thread that structure is irrelevant and distracting. The box notation is so much better. Mark, you argue that "apparently 'syncopated' rhythms sometimes have an inner logic other than as a superficial displacement of events in a rhythmic pattern whose deep structure is evenly divisive." Any appeal to standard European metres might only impede our achieving that insight.
Aaron Davies said,
May 10, 2009 @ 7:56 am
desperately resisting the urge to make a terrible pun involving "accidentals"…
Coby Lubliner said,
May 10, 2009 @ 10:16 am
Noetica: it wouldn't be "septave" but "septim" if you use the Latin ordinals as a basis.
Noetica said,
May 10, 2009 @ 11:09 am
…it wouldn't be "septave" but "septim" if you use the Latin ordinals as a basis.
Absolutely right, Coby. In fact OED records septime, with a slightly different motivation:
But this time I went with the barbarous septave, since it has modern precedent here and in several other places, though OED does not include it.
tathagata said,
May 10, 2009 @ 1:18 pm
The rhythm in Monteverdi's Orfeo is omnipresent in music of that time.
[(myl) Do you mean hemiola, or the specific 1+1+2+1+2+1+2+2 sequence of Vi Ricorda? Hemiola, as discussed in the post, was certainly very common in Monteverdi's time, and continued to be common through the Baroque period and beyond. The specific quasi-galliambic rhythm of Vi Ricorda is another matter.]
Similar syncopations occur in Martin Luther's hymns and other German lieder from that period, for example. No particular connection can be made between monteverdi's usage of that rhythm and orfeo. Mozart even makes reference to similar rhythms in the duet between Masetto and Zerlina with chorus, #5 in Don Giovanni.
[(myl) Which hymns do you have in mind? As for the aria #5 in Don Giovanni, it's in 6/8 time and exhibits occasional 2+2+2 vs. 3+3 hemiola patterns, but I don't see anything in it that matches the very specific time-interval sequence under discussion here.]
Both the Mozart and the Monteverdi are used to represent a joyful atmosphere in anticipation of marriage, while the German version shows up in the contemporaneous version later set to the text "O sacred head now wounded". The ubiquitous appearance and expressions of this rhythm suggests it is unexceptional.
Noetica said,
May 12, 2009 @ 12:40 am
Mark wrote:
And Scratchdaddy wrote:
Some sort of many-stranded Phrygian connexion has indeed been thought likely, as this rather voluble source suggests:
There remains a great deal of uncertainty about the detailed derivation of our Cybelic gallus. Other galli include, of course, "native of Gaul" and "cock". Strangely enough, we find this for the cock version in Lewis and Short:
And then this from LSJ:
This association with strident vocalisation gives a plausible alternative foundation for the many accounts of Galli that cryptically link it to mad raving – alternative to this, I mean, from Lewis and Short:
That should put the cap on it.
Bill Walderman said,
May 14, 2009 @ 8:59 am
I agree with Tathagata. I've listened to a lot of Monteverdi and Frescobaldi and the rhythm of Vi Ricorda strikes me as characteristic of the music of the period. I can't cite chapter and verse, by Vi Ricorda doesn't seem at all unusual when I listen to it.
[(myl) Specifics would be much more helpful here than general impressions. It's obvious that hemiola was common in music of that period — but it's not clear how common the specific per-verse-line pattern 1+1+2+1+2+1+2+2 was. Unless you can give some specific examples, I'll continue to be skeptical of your general impression. Let me try to make the issue clearer with an analogy — if we were interested in the history of the limerick form, the observation that Homer used dactyls would not be specifically relevant, nor would a general feeling that the limerick rhythm "strikes [someone] as characteristic of" (say) the poetry of 17th century Italy.]
And I also agree that it's a mistake to try to fit rhythms from the Monteverdi era–and even more so, the meters of classical Greek and Latin poetry–onto the Procrustean bed of 18th and 19th century European classical music.
The "anaclastic" meter that is similar to Vi Ricorda is used in a number of Greek poems attributed to Anacreon (6th c. BCE) and other Greek poems that are generally dated (without much confidence) to the Imperial period (200-500 CE) written in imitation of Anacreon (the so-called Anacreontea). I'm not sure that the conventional analysis of this meter, which is derived from ancient writers on metrics, as ionic dimeter with anaclasis (reversal of heavy and light syllables) is correct. Some of these poems use a catalectic form of the meter, with just one light (or "short" if you prefer) syllable at the beginning of the verse, which suggests to me that the meter is simply a structure that doesn't lend itself to further analysis in terms of smaller units, despite the efforts of the ancient (and some modern) writers on metrics to do so.
Maybe there's a connection between Vi Ricorda and the Anacreontea (though I think that Vi Ricorda is simply a rhythmic pattern that was prevalent in Monteverdi's era), but I don't see any grounds for connecting Vi Ricorda to the galliambic meter of Catullus 63, given that the "anaclastic" meter exists as an established meter without the second half of the galliambic meter.
[(myl) The Cybele cult was introduced into Italy in 204 BC, and as far as I know, it continued to be practiced until the 4th century AD, when the imposition of Christianity presumably suppressed it. That's 500-600 years for song forms to diffuse into popular culture. I don't have any evidence that they did, but it seems plausible that they might have.
Monteverdi might have invented this rhythm all on his own; he might have been imitating Greek models rather than Catullus; he might have been using a folk meter influenced by the chants of the Galli; or none of the above. My point was just to note the similarity. ]
One other point is worth thinking about: the analysis of the anaclastic meter and the two halves of the galliambic meter set forth above seems to depend on the ability to substitute two light (or short) syllables for one heavy (long) syllable, as in the hexameter, but many other ancient Greek (and Latin) meters were isosyllabic and did not admit this substitution–instead, many meters permitted "anceps" syllables (syllables that could be either light or heavy)–particularly the Aeolic meters such as the glyconic, which began with a so-called "Aeolic basis" (two or one anceps syllable). This draws into question the general validity of the analysis suggested above, which assumes that each verse must be isomoric (with one mora equal to a light syllable). At any rate, ancient metrics is (are?) a very confused subject and much of the conventional analysis seems like an effort to fit round pegs into square holes.
Also I'm not sure there is any connection between Orpheus and the Cybele cult. In fact, in line 69 of Cat. 63, Attis describes himself as a "Maenas," which is just the opposite of identification with Orpheus.
[(myl) Eurydice is not exactly Cybele either. But the idea of the connection isn't mine, it goes back at least to Fraser's Golden Bough (see the link in the post). ]
Bill Walderman said,
May 14, 2009 @ 12:17 pm
It's also noteworthy that some of the poems attributed to Anacreon and poems of the Anacreontea are in a meter that is similar to the "anaclastic" meter but each verse begins with an anceps syllable instead of two light (short) syllables. This is conventionally described as "iambic dimeter catalectic" (i.e., an iamb, a h l h, followed by a catalectic iamb, i.e., l h h, where a=anceps, h=heavy and l=light). In view of the similarity between the "ionic dimeter catalectic" and "anaclastic" meters, it seems better to view the verses of these two meters as integrated rhythms that shouldn't be analyzed in terms of smaller units–which would results in two very different analyses–and that are part of a family of similar rhythms. On that analysis, the "anaclastic" meter would be viewed as an independent rhythm that shouldn't be seen as a manipulation of some other basic underlying pattern. I would also avoid the term "syncopation" in discussing classic Greek and Latin meters–it's a term that applies to Western music of the 18th-20th centuries (including jazz, of course), where there are regular measures with basic rhythmic patterns but doesn't necessarily contribute to the analysis of rhythms from other periods and cultures.
[(myl) The original issue under discussion is how to think about tune-text alignment in various genres of 20th-century popular music, where strong syllables in the English text often fall off the "beat" in the music, at least according to traditional treatment of (say) 4/4 time as a hierarchical alternation of strong and weak units. (Of course, various of the musical parts may also seem to be "syncopated" in that sense.) David Temperley has suggested (see the post for links) that the underlying structure in such cases is the regular alternating pattern, with a stylistic process that shifts some events off the beat (typically moving them earlier in time). There are some good arguments on his side, and an analysis of this kind may be the right one in some cases. But there are also reasons to see non-isochronous event patterns as a basic metrical form in some traditions, and I think that 20th-century American popular music may be (at least partly) one such.
In the case of (most kinds of) African music, there are certainly "regular measures with basic rhythmic patterns". And the "regular measures" are generally 8 or 12 or 16 time-units long — not 7 or 11 or 17 or whatever, as the repeating patterns may be in some traditions of "additive rhythms". But the subdivisions of the 1/12/16-unit measures (a) don't always subdivide the measure into equal subparts, and (b) typically exist at several different levels that do not entirely intersect.
As for the galliambic and related poetic meters, my argument is that they correspond to music meters of a somewhat similar kind, where a repeated "measure" of (in this case) 12 time-units is subdivided in a way that is not isochronous. The implication of terms like "acephalic" and "catalectic" is that positions in the (musical) meter are unrealized, i.e. replaced by rests in the (metrically aligned) text.
We seem to be speaking somewhat at cross-purposes — that is, I think you're largely agreeing with me, but you write as if you weren't. Have you read the post and the earlier one that it links to? ]
Bill Walderman said,
May 14, 2009 @ 3:58 pm
Prof. Liberman: I think we are in agreement, though I fear my comments were unnecessarily argumentative. My point is simply that, as you say, the anaclastic and similar rhythms are best seen as "basic metrical pattern[s] in which events don't fall at evenly-spaced time intervals" rather than as "the displacement of events from an underlyingly regular meter." In vol. II of Campbell's new Loeb Greek Lyric (not Edmond's atrocious old Lyra Graeca), there's a very good introduction to Anacreon and the Anacreontea. The metrical discussion analyzes the meters in conventional terms as displacements of underlying regular meters, but in my view you can see clearly that the meters are all part of a "family" of similar rhythms, which the conventional analysis obscures. For Greek meters generally, see M.L. West, Greek Meters (Oxford 1982). The conventional analysis is based on ancient writers on metrics, but they were writing many centuries after the meters themselves emerged in poetry.
I don't think that terms such as "acephalic" and "catalectic" don't necessarily imply rests–they're simply analytical attempts (possibly misguided) to derive one meter from another by lopping off a syllable at the beginning or the end.
I think that those of us brought up in the tradition of Western "classical" music of the 18th and 19th centuries may have a tendency to shoehorn irregular rhythms into patterns of underlying regularities where they don't belong. Applying the term "syncopation" to irregular rhythms of music that belongs to different traditions is perhaps symptomatic of this tendency.
One more point: without being disrespectful I don't think Fraser's wildly fanciful Golden Bough, which sees connections everywhere, especially where mystery cults and fertility goddesses are concerned, is very sound authority for linking Cybele/Attis to Orpheus.
I'll try to find something about the rhythms of the Monteverdi era, though I doubt I'll have the time to do justice to this question. I'd urge you to listen to some Monteverdi if you're not already familiar with his music, and also Frescobaldi, though, not just as a research project but to experience some wonderful music. Book 8 of the Madrigals is the most advanced. If you enjoy heart-breaking, aching dissonances, try Gesualdo, especially Books 4 and 5. For exciting irregular rhythms that defy attempts to impose underlying regularities, Bartok Quartet #5 and the Ligeti Piano Etudes.
Noetica said,
May 16, 2009 @ 1:38 am
Well Bill Walderman, I've been looking through as much of the background material as I can conveniently assemble and assimilate, and I find myself agreeing on this general point that you make (which I touched on earlier myself, in fact):
Somewhat similarly, it seems that even basic terms like metre and rhythm come laden with different suppositions in language (including literary analysis) and music. In both areas, even the basic definitions are contested. New Grove cites Sachs (Rhythm and Tempo, 1953, p. 12), concerning just rhythm:
It is valuable to step back and analyse freshly the supposed isomorphisms even within just one of these two areas. Within music, take this matter of "the Bembé rhythm [being] curiously isomorphic to the (major) diatonic scale", mentioned by Mark in the initial post. How are elements in the domains of pitch and duration truly aligned (or notionally alignable, without risk of some sort of category error)? Here are two broad elements in the domain of time, at least in traditional Western analysis:
1. metre [like 4/4]
2. rhythm [like the temporal pattern of thirteen onsets in Mark's excerpt from "Here Comes The Sun",* the onsets being located with reference to that 4/4 metre]
(*Incidentally, the melody in Mark's earlier post needs correction, I think. The G# ought to be an F#.)
Simple, so far: that rhythm is "embedded" in that metre, even if it subverts the more common expectations associated with 4/4. (Along the way we observe a difference between musical and "linguistic" metre. Linguistic metre, as you and Mark have uncovered, can be interpreted in more ways than Western musical metre can be.) But now, here are three broad elements in the domain of pitch (leaving out some important intermediates), in traditional Western analysis, using terms of my own choosing:
1. scheme of division of the octave [like the standard (and let's say equal-temperament) 12-tone division of common practice]
2. scale [like the diatonic scale A major, a selection of seven type pitches from that scheme]
3. sequence of pitches [(distinct from melody, which must involve rhythm as well as pitch) like the sequence of thirteen token pitches in Mark's excerpt from "Here Comes The Sun": all selected from that A major scale]
Sure – Pressing and several other authors find an analogy between Bembé in the domain of time and the (major) diatonic scale in the domain of pitch. But then, is Bembé truly comparable to a scale (the primary application of the term diatonic), or to a sequence (since it is experienced as a matter of succession of real sounds, just like the sequence of pitches in "Here Comes The Sun", and not a mere abstract template with which something more delimited must fit)? Trying the first way, things line up like this:
scheme > scale [12-tone division > diatonic scale; say, A major]
metre > rhythm [12-point cycle > Bembé]
But then, there is nothing to correspond with the natural next phase in explicating how diatonic behaves as applied to pitch:
scale > sequence [diatonic scale of A major > sequence of thirteen pitches from "Here Comes The Sun"]
rhythm > ? [Bembé > ? ]
There are also difficulties if we take Bembé, at least equally plausibly, as analogous to what I have called a sequence, since in the domain of pitch that is not what diatonic is: diatonic is a kind of scale.
Last, if this sort of analogising is indeed so problematic, and cultural baggage is to be left in the locker at the airport, why is anyone even tempted to call Bembé a matter of "ternary rhythm" in the first place? An eminently disposable notion, as obiter dicta in the literature suggest. It certainly doesn't fit at all comfortably with our Western notions of three-way divisions of time.
Gary Harding said,
October 8, 2010 @ 5:34 pm
I see that on this discussion page my work product and specific terms from it have been used without proper citation.
Could you please include this link when you mention "the Seven Wheels of Bembé", Bembé Wheel or any variation thereof?
http://www.myspace.com/thesevenwheelsofbembe
I've put together a small myspace site to clear up some issues that revolve around "the seven wheels concept" both musical and legal:
"The Seven Wheels of Bembé were developed in 1968 by Gary Harding and were first published in 1972 in an NEA grant awarded him while an instructor of music and Chicano Studies at Washington State University. The concept has been used with/without permission throughout the internet. However, even the best descriptions have problems. This posting is presented to clear up these rhythmic issues, as well as, to set the record straight as to copyright and intellectual property prerogatives. Any reference to "bembé wheels" or "the seven wheels of bembé" should include a proper citation of the author, Gary R. Harding. – "Cuban and Brazilian Hand Drumming" Alemao Press 1994, Seattle, Washington page 48"
Thank you