Most bibliography
« previous post | next post »
Thanks to several commenters on our recent most-a-thon ("Most", 7/31/2010; "Most examples", 7/31/2010; "Most and Many", 8/1/2010), I've learned about an interesting literature on the semantics, pragmatics, and psycholinguistics of most, which I think is worth collecting in one place for those unexpectedly unobsessive readers who don't repeatedly scan and cross-classify the comments on this kind of Language Log posting sequence.
These publications provide a variety of (mostly perceptual) evidence for the view that most really does mean "more than half", while offering a greater variety of theories about the strategies that (different sorts of) people use to determine whether this is true in particular cases.
In the face of these results, it remains puzzling why so many people think that a proposition like most X's are P imposes extra requirements, for instance that P-ish X's are a supermajority, or that P is the default state for X's. There are two obvious stories to tell about this: perhaps it's simply an illusion, and these extra meanings are just conversational implicatures arising in the usual way in certain contexts; or perhaps such meanings, having started out that way, have become conventionalized by some speakers. The variationist view is intrinsically plausible — word meanings drift in this way all the time — but if super-mosters or default-mosters were as common as they seem to be, you'd think that the several experiments described below would have run into empirical difficulties with a substantial subset of subjects. Which doesn't seem to have happened…
Yesterday evening, Itamar pointed us to Martin Hackl, "On the grammar and processing of proportional quantifiers: most versus more than half", Natural Language Semantics 17:63-98, 2009.
Hackl argues that most basically means "the largest subgroup bigger than any other subgroup" (which thus retains its etymological semantics as the superlative of more, while having the same truth conditions as "more than half" when there are just two subgroups). From Hackl's conclusion:
In the case of quantification, fulfilling this obligation [to furnish the pieces that processing theories require to draw systematic distinctions that occur during real time comprehension] hinges on what type of semantic primitives one assumes for quantification in natural language. A compelling example is provided by the pair most and more than half, which are standardly treated as truth-conditionally equivalent quantifiers. I presented experimental evidence from real time verification studies that differentiates these two expressions in ways that seem to correspond to specific differences in their form – the former being a superlative and the latter a comparative expression of proportions. […]
Specifically, I offer a compositional analysis of MOST as the superlative of MANY, arguing that the proportional reading is in fact a special case of the superlative reading. Extending the analysis to FEWEST offers an explanation for a currently unexplained systematic gap in the paradigm of proportional quantifiers, namely that FEWEST cannot be used as a proportional quantifier. Such an analysis presupposes that the set of semantic primitives of quantification includes e.g. degree expressions, measure phrases, and comparative and superlative operators but not relations between sets as GQT would have it.
This afternoon, Rachel directed our attention to Tim Hunter, Justin Halberda, Jeffrey Lidz, & Paul Pietroski, "Beyond Truth Conditions: The Semantics of most", SALT2008. (I'm ashamed to say that I discussed this paper, at modest length, in a post more than two years ago, "Sexual pseudoscience from CNN", 6/19/2008 — and then forgot about it until Rachel reminded me.) They take up Hackl's analysis, and (while basically agreeing with his characterization of the meaning of most), take the argument in a different direction:
In this paper we have argued against the claim that a competent speaker’s understanding of a sentence is exhaustively characterised by a truth condition. To do so we have presented evidence of asymmetries in speakers’ willingness to use various verification procedures: in Experiment 1, an apparent bias to use algorithms approximating a cardinality comparison rather than those based on one-to-one correspondence, and in Experiment 2, an insistence on an indirect method of approximation. These asymmetries would be surprising if the only constraint on the choice of verification procedures for a sentence was the requirement that the procedure must implement the sentence’s truth condition.
Back in June of 2008, I wrote this:
There's some experimental evidence that most people mostly interpret most in a way that lends itself to an easy transition to the generic plural. One piece of the puzzle: Tim Hunter, Justin Halberda, Jeff Lidz & Paul Pietroski, "Beyond Truth Conditions: The semantics of 'most'", SALT 18. They examined people's responses to statements like "Most of the dots are yellow", for displays in which the proportions of yellow and blue dots ranged between 1:1 and 2:1. They concluded that people interpret most in terms of a comparison of cardinalities mediated by the "Approximate Number System" (ANS), as discussed in Lisa Feigenson, Stanislas Dehaene and Elizabeth Spelke, "Core systems of number", Trends in Cognitive Sciences, 8(7): 307-314, 2004. Thus "participants' success rate … decreased as the ratio of the number of yellow dots to the number of nonyellow dots approached 1, closely matching the psychophysical function independently identified for the ANS".
According to Feigenson et al., there are two core cognitive systems dealing with numbers: an approximate representation of numerical magnitude, and a precise representation of distinct individuals. Perhaps linguistic equivocation between these systems — as well as the inadequacy of either system to express even simple propositions about statistical distributions — helps to explain the general tendency to derive propositions about generic group characteristics from propositions about differences between group averages, even when these difference are small relative to within-group variation.
And this evening, Alexander told us about Lidz, Pietroski, Hunter & Halberda, "Interface Transparency and the Psychosemantics of 'most'", Natural Language Semantics, 2009.
Alexander's description:
Among other things, Lidz and colleagues have psychophysical data showing that people, when shown an array of blue and yellow dots for a very brief time, and asked to respond immediately, Yes or No, whether most of the dots are blue (or yellow, etc.), consistently respond as if the question is whether >50% are blue (or yellow, etc.). They do not demand a big fat majority. This sort of data is interesting, in being different than either usage data from corpora, or data from responses to pragmatically contextualized questions.
From the start of their abstract:
This paper proposes and defends an Interface Transparency Thesis concerning how linguistic meanings are related to the cognitive systems that are used to evaluate sentences for truth/falsity: a declarative sentence is semantically associated with a canonical procedure for determining its truth value (cf. Dummett 1973, Horty 2007); and while this procedure need not be used as a verification strategy, competent speakers are biased towards strategies that directly reflect canonical specifications of truth conditions. Evidence in favor of this hypothesis comes from a psycholinguistic experiment examining adult judgments concerning ‘Most of the dots are blue’.
This sentence is true if and only if the number of blue dots exceeds the number of
nonblue dots. But this leaves many issues unsettled—e.g., how the second cardinality is specified for purposes of understanding and/or verification: via the nonblue things, given a restriction to the dots, as in ‘|Dot(x) & ~Blue(x)|’; via the blue things, given the same restriction, and subtraction from the number of dots, as in ‘|Dot(x)| – |Dot(x) & Blue(x)|’; etc. We obtained evidence in favor of the second hypothesis.
A bit of poking around in Google Scholar turns up a number of other interesting papers, including Halberda, Taing, and Lidz, "The Development of 'Most' Comprehension and Its Potential Dependence on Counting Ability in Preschoolers", Language Learning and Development 4(2):99-121, April 2008:
Quantifiers are a test case for an interface between psychological questions, which attempt to specify the numerical content that supports the semantics of quantifiers, and linguistic questions, which uncover the range of possible quantifier meanings allowable within the constraints of the syntax. Here we explore the development of comprehension of most in English, of particular interest as it calls on precise numerical content that, in adults, requires an understanding of large exact numerosities (e.g., 23 blue dots and 17 yellow is an instance of “most of the dots are blue”). In a sample of 100 children 2 to 5 years of age we find that (a) successful most comprehension in cases with two salient subsets is achieved at 3 years, 7 months of age, and (b) most comprehension is independent of knowledge of large exact number words; that is, knowledge of large exact number words is neither necessary, as evidenced by children who understand “most” but not “four,” nor sufficient, as evidenced by children who understand “nine” but not “most.”
Also Pietroski, Lidz, Hunter, and Halberda, "The Meaning of 'Most': Semantics, Numerosity and Psychology", Mind and Language, 24(4):554-585, 10/26/2009:
The meaning of 'most' can be described in many ways. We offer a framework for distinguishing semantic descriptions, interpreted as psychological hypotheses that go beyond claims about sentential truth conditions, and an experiment that tells against an attractive idea: 'most' is understood in terms of one-to-one correspondence. Adults evaluated 'Most of the dots are yellow', as true or false, on many trials in which yellow dots and blue dots were displayed for 200 ms. Displays manipulated the ease of using a 'one-to-one with remainder' strategy, and a strategy of using the Approximate Number System to compare of (approximations of) cardinalities. Interpreting such data requires care in thinking about how meaning is related to verification. But the results suggest that 'most' is understood in terms of cardinality comparison, even when counting is impossible.
And Jon Gajewski, "Superlatives, NPIs and Most", Journal of Semantics 27(1):125-137, 2010:
The ability of English determiner most to license negative polarity items (NPIs) has long stood as a puzzle for theories that follow Ladusaw (1979) in claiming that NPIs must appear in the scope of downward entailing (DE) operators. Most licenses NPIs such as any and ever in its restrictor but is not downward, or upward, entailing with respect to its restrictor. In this paper, I argue that despite appearances to the contrary, NPIs in the restrictor of most are in the scope of a DE operator. I make crucial use of a recent proposal by Hackl (2009) to compositionally analyze determiner most as a superlative expression. When the semantics of the superlative morpheme is spelled out correctly, this derives the result that most licenses NPIs in its restrictor.
Amerloc said,
August 2, 2010 @ 8:49 pm
The third paragraph made me laugh, just because of the multi-syllabic jargon employed (to good effect – don't get me wrong).
I cherish unexpected chuckles, so I thank you.
axl said,
August 2, 2010 @ 10:29 pm
what do you mean by "mostly perceptual"?
[(myl) They asked people to judge (for example) whether a collection of dots was "mostly blue". I'd call that a perceptual task. They didn't (for example) ask people to describe a collection of dots, to see how often they said it was "mostly blue". That would have a been a production task.]
does any of this cf. to "mainly"? Or am I late on the train?
[(myl) Sorry, I don't understand. If you're asking whether this post is also about "mainly", it's not. If you're asking whether these papers also discuss "mainly", you're welcome to read them and see.]
Jerry Friedman said,
August 2, 2010 @ 11:48 pm
That seems persuasive, but I'd like to try to save "super-most". (Yes, I'm biased.)
Both the Hackl paper and the Lidz et al. paper start with the assumption that most means more than half. The Lidz paper studies the fraction of answers that were "incorrect". Is it possible that some people correctly saw that there were 12 blue dots and 10 yellow dots, but "incorrectly" said it wasn't true that most were blue? Or that people picked up cues that said they were supposed to understand most that way? Or that some people asked, "What do you mean by most and were told, "More than half"? (I can't be the only smart-aleck in the world who would start by asking that question.)
I'd be more convinced by an experiment that was designed to elicit the meaning of most, without preconceptions on the experimenters' part.
If nothing else, there might be a sociolinguistic effect. Let's say Lidz et al.'s "twelve naive adults" really do all understand most to mean more than half. The difference from the Language Log population is striking.
[(myl) It certainly seems to me that a random sample of LL commenters, acting according to the intuitions that commenters have expressed about when they would license the use of "most", would have given results in all of these experiments that are rather different from the results that that the experimenters actually got.
It's possible that the subjects were drawn from a pool that's somehow different. And it's possible that the subjects were somehow influenced by the experimenters' prior beliefs about the meaning of "most".
But neither of these hypotheses seems very probable to me.
I'm inclined to think that it's really true that a random sample of American college students, asked whether "most of the dots are blue" (or whatever), tends to respond "yes" if (they perceive that) more than half of the dots are blue.
And I'm inclined to think that the intuitions of the super-mosters and the default-mosters, though genuine, may be driven by Gricean considerations ("Why would I say 'most' when that imposes so little constraint on the proportion? If I know that it's about 55%, it would be much more informative to say 'a bit more than half' or even simply 'more than half', with the implicature that it's not probably not a lot more than half, or I'd have said something else; if I know that it's 95% or so, it would be much more informative to say 'nearly all'; if the only thing that I know is that it's more than 50%, I should say exactly that; so I'll reserve 'most' for (a) the area around 70% or 80% (details depending), or (b) for the case where I don't know much about the proportions, but think that the property being quantified is characteristic of the set under discussion."
Also, note that if Hunter et al. are right to argue that people interpret most in terms of a comparison mediated by the "approximate number system", then that's a step on the way to treating most as an approximation to the generic plural. )]
Jerry Friedman said,
August 2, 2010 @ 11:53 pm
P. S. Before anybody jumps on me from either side, I think of persuasive as weaker than convincing. I've gotten in trouble for this before.
Rick S said,
August 3, 2010 @ 2:48 am
Like Mark, I did a double-take on John Irving's "I wouldn't say 'most' but I'd say 'more than half'". However, during the ensuing discussion (in which I haven't previously participated) I found myself aligning with the super-mosters. Those sound like incompatible positions, but I resolve the conflict by reference to implicature. Where the context sets up a logical proposition (as in "most of the dots are yellow"), the Maxim of Quantity positions me to interpret "most" as >50%. This is especially true in an experimental setting, where I'm not a conversational participant and don't get to negotiate the implicatures. Where no answer set is implied, I'm free to use finer-grained semantics of "most". I feel certain that if the SALT18 experiment had offered choices "about equal, mostly blue, mostly yellow"–perhaps even "a bit more blue" and "a bit more yellow"–the results would have been very different. (Alternatively, a "strongly agree" to "strongly disagree" answer scale could have been used with the original proposition.) In other words, the binary nature of the proposition carried an implicature that "most" means ">50%" in this context.
In Irving's interview, Andersen's question sets up a "most"/"not most" (or, equivalently, "in English/not in English") logical proposition, so we expect Irving to affirm or refute it. But Irving already had an established cognitive framework for the concept of his readership distribution–reflected in his original statement which Andersen "read somewhere"–in which he was clearly using finer-grained semantics, since he interrupted to correct Andersen's "most" to "more than half". So Irving's response changed the implicature, which is what caused our double-take.
Kylopod said,
August 3, 2010 @ 5:04 am
I'm wondering about the extent to which people use "most" in an imprecise way simply to oversimplify things and manipulate the conversation.
Take the frequent claims about Al Gore and the 2000 election. I have heard many people assert that Gore got a "majority" of the popular vote. In fact, he only got a plurality–48% to a slightly lower 48% for Bush. The use of the word majority to mean "plurality" is widespread, and understandable since the former is a lot more common word. This perspective gets even further off the ground when people assert that "A majority of Americans" voted for him, apparently forgetting about Americans who didn't vote, some of whom weren't even eligible to vote.
The final absurdity comes when you hear that "Most Americans voted for Gore," which gets about a half-dozen hits on Google, plus 10 if you call him "Al Gore." This may not be that common an assertion, but it's built on a lot of the assumptions people make when they use these words. "Most" translates to "majority," and "majority" translates to "plurality," and non-voters don't exist. In reality, probably only a tiny minority of Americans actually voted for Gore, but because it was unquestionably more than the amount who voted for Bush, it comes out in at least a few people's minds as "most."
In my view, what leads people to this type of assertion is not simply how they define the words. It has to do with what they think of the results of the election. In the U.S., presidential elections are determined by the electoral college, not the popular vote, but having a popular-vote loser win the presidency is very uncommon (the last time it had happened was 1888), and even the electoral college results in 2000 were mired in controversy over the vote-counting in Florida. Many people (myself included) believe that a fair count of the votes in Florida would have shown Gore to have won the state, and hence the election. So it really isn't about the national popular vote. Asserting that "Most Americans voted for Gore" is a way of trying to cast a sense of illegitimacy over Bush's rise to the presidency, but without having to argue the specifics that really matter. The 1888 election, in contrast, was never in doubt, even though the winner had lost the popular vote. You can certainly argue (as I would) that the electoral college is a terrible system, but that's a different subject for a different time.
People who don't believe the election was stolen from Gore are not likely to assert that "most" or "a majority of" Americans voted for him, but some of those same people might use the word "most" when describing Bush's 2004 victory where he got 51%.
So it isn't necessarily that people are redefining the word "most" or even "majority" to mean "plurality." Rather, people use these words in those senses when they wish to oversimplify points. In other words, it says a lot more about what the speaker is trying to prove than whether the speaker uses these terms consistently in a broad sense. I suspect that most people do not normally define "most" to include a slight majority, much less a plurality, but they're willing to adopt this expansive definition on occasion, often when they're engaging in rhetorical sleight of hand.
Karen said,
August 3, 2010 @ 5:57 am
For me, personally, I'd say "most" of the dots were blue if I was asked to judge that task. I understand that "most" means "more than half" in some contexts. But for me, it's useless as a word conveying information if I don't know if that's 51 or 99 percent, so as MYL suggests, I reserve using it for, I'd guess, 85-95 percent (otherwise saying things like "more than half" or "almost all" or "three out of four"). And I ask when I hear it.
mollymooly said,
August 3, 2010 @ 5:58 am
@Kylopod:
In British parliamentary language, the gap between first place and second place is a "majority", "simple majority", or "two-party majority); the gap between first place and everybody-else-put-together is an "overall majority". The British plurality voting system is called "first past the post", so few people ever encounter the word "plurality" at all.
A constituency votes for an MP by simple majority, whereas MPs vote for a Prime Minister by overall majority. This muddied the discourse after the recent general election, where the Conservatives had a plurality of seats but not an overall majority; a situation sufficiently rare to have the scary name "hung Parliament".
Nick A said,
August 3, 2010 @ 7:46 am
In response to Kylopod:
Use of quantifiers like 'most', 'some', 'all', 'none' generally involves implicit narrowing of the scope of the quantifier. Famous examples:
(1) I've got nothing to wear.
Meaning: I've got nothing (suitable) to wear.
(2) Everyone came to the party.
Meaning: Everyone (who counts in some way) came to the party.
If I say:
(3) Most people voted for Bush in 2004
I might mean (and expect you to realise that I mean), 'Most people (of those who voted) voted for Bush in 2004'.
It's a bit more of a stretch, but not impossible to imagine that someone saying:
(4) Most people voted for Gore in 2000
means 'Most people (of those who voted for Bush or Gore) voted for Gore in 2000'.
Of course, it's open to the hearer of such an utterance to respond along these lines: 'No, it's not the case that most people voted for Gore in 2000. He got more votes than Bush, but not a majority of the votes cast,' in the process implicitly rejecting the intended narrowing of quantifier scope.
I don't deny that there is a difference in acceptability between (3) and (4). I just want to suggest that it depends on what quantifier scope narrowing is readily performed by hearers, and that is a pragmatic matter, (i.e.) highly sensitive to context.
Nicholas Waller said,
August 3, 2010 @ 9:45 am
@ Nick A – "(2) Everyone came to the party."
This reminds me of an old MAD cartoon (Dave Berg, I think) in which a teen is scouring the vast crowd at a baseball game and failing to spot any of his friends: "There's nobody here!"
DJR said,
August 3, 2010 @ 9:55 am
As a lawyer, the ambiguity of "most" is useful. If I wanted to convince a judge that my position was correct, where 10 courts ruled my way and 9 courts ruled the other way, I would say: "Most courts to have addressed this question have held …" because "most" does not make it seem like the question is close. Of course, "majority" can be used the same way: "A majority of courts have held …" is more convincing than "Ten of nineteen courts have held …" even though they are equally true.
A similar question arises as to "consensus." An online dictionary tells me "consensus" means a majority of opinion. Could I say, "The consensus view of the courts to address the question is …" when the courts are split 9-10? Or is a supermajority required for consensus? In some systems, decisions made by consensus are made without objection, so in fact a "consensus" means 100%.
Kylopod said,
August 3, 2010 @ 10:49 am
@Nick A
Reading it as "Most people (of those who voted for Bush or Gore) voted for Gore" might make marginal sense within the context of this particular election, since Bush and Gore were the only candidates with a remotely serious chance of winning, and they both came close to reaching the majority of the popular vote. But this kind of wording becomes harder to justify when there are several serious candidates, and the plurality could go to someone in the 30% range or even lower.
@Nicholas Waller
Then there's the classic, after a head injury–"They examined my head and found nothing."
Russell said,
August 3, 2010 @ 11:27 am
One might also add this to the bib list:
Ariel, Mira. 2004. "Most" Language 80.4 (658-706)
I haven't read it, but if it is similar to the chapter on "most" in her recent Cambridge textbook, it will argue (in part) that "most" has a semantic (not pragmatic) upper bound, i.e., 50% meaning as given.
Russell said,
August 3, 2010 @ 11:30 am
Somehow some of my comment got truncated. I mentioned that there are several responses in the literature to Ariel's claim (which you can find conveniently with Google scholar), but one worth mentioning is
Horn, Larry. 2006. The Border Wars: a neo-Grican Perspective. In Where Semantics Meets Pragmatics (von Heusinger and Turner, eds).
Russell said,
August 3, 2010 @ 11:35 am
Wow, talk about a totally newbie error with angle brackets.
Anyway…The claimed semantic upper bound is <100%, not ">50% meaning as given." (but it is true that Ariel and Horn take the >50% part of the meaning as given.)
[(myl) Here's the abstract for Mira Ariel, "Most", Language 80(4) 2004:
And from Larry Horn, "The border wars: a neo-Gricean perspective", 2006:
Please note that "impliciture" is not a typo, but rather a reference to Kent Bach, "Conversational Impliciture", Mind & Language 9: 124-162, 1994. ]
Boris said,
August 3, 2010 @ 12:45 pm
I alway thought consensus means that everyone agrees. Where it does not mean that, it means something like "everyone who matters in this case agrees". Otherwise what would it mean to "break the consensus"?
grackle said,
August 3, 2010 @ 2:17 pm
In the two studies linked, I'm bothered by two things: (1) that in a brief (as described) view of yellow and blue dots there seems to be no control for the relative intensity of color and how that might affect perception. It doesn't seem to me that colors are neutral items in comparisons like these. (2) Particularly in the second study linked, my impression is that there was no choice other than that of "most of". If the participants had been allowed to make the choice "more of the dots are x" rather than "most of…" what would the results have shown? When one is given only a choice that either x or y is "most of" the result is predetermined. I suppose I am only restating the objection in the comments above that the studies are biased toward most=>50%.
groki said,
August 3, 2010 @ 7:59 pm
[I am really enjoying (am most pleased with, in the way-over-half sense) this multi-threaded discussion–especially the way it reveals interesting and surprising differences among speakers of the "same" language. many thanks to the posters and all the commenters.]
+1 on the feeling of experimental bias. (but then my way-over-half* ox is on the skewer here. :)
it's not a simple either-or for me: in the dots experiment, I too would say that most is accurate even when it's only a bare majority–since there are only two choices.
but there's more going on, it seems to me introspectively. in this regard DJR's lawyerly comments resonate strongly. ("a little shifty" indeed!)
maybe there's a statisticsy issue here: for us way-over-halfers, bare-majority could feel (to an imprecisely formulated and maybe variable greater or lesser extent) like it might just be one of those damn lies.
or could it be some kind of very rough analog of "average" being ambiguous as to mean, median, or mode?
[*my sense of "most", for what it's worth: the center of my most is in the high-percentage-so-representative-of-class realm. bare-majority is a boundary on the low end: still techincally correct, but also somehow a fraught choice (unless it's the only one). on the other end, 100% feels just past the high boundary (but even there I might use most to mean something like "I think it's all, but maybe there's something I haven't thought of": sort of a "margin of error" allowance). and close to 100%, "virtually all" or "almost entirely" seem like better (less fraught) choices than "most."]
Garrett Wollman said,
August 3, 2010 @ 10:52 pm
Agree with those who suggest that the dot experiment as set up introduces a bias; most people are aware that "technically", "most" can mean (is used by some to mean) "more than half". Particularly in experimental settings, I would expect this meaning to be inferred by subjects even when not explicitly stated by the experimenter. I would be more interested in an analysis of "most" usage from LDC's telephone corpus, for example — although it would require a great deal of work to tease out the actual meaning intended in such circumstances. It might also be possible to identify the cases in which conversation partners disagree as to the meaning.
stephen said,
August 3, 2010 @ 10:59 pm
Here's something related in a book called Hodge-Podge: A Commonplace Book, by J. Bryan, III, from Ballantine, 1986.
It's a collection of trivia, anecdotes and quotations.
On pp. 43-44 he has a quotation from Robert Graves and Alan Hodge, The Reader over Your Shoulder.
"There is a popular measure of proportion, with approximate percentages as follows:"
(100%) Mr. Jordan's fortune consisted wholly of bar-gold.
(99%) Practically all his fortune consisted of bar-gold.
He goes down a list, giving percentages for different descriptions of how much of Mr. Jordan's fortune is bar-gold. But "Most" isn't in the list.
70% is "the greater part of his fortune."
The list continues with more than half; rather more than half; half; nearly half; a large part; quite a large part; a considerable part; and so on.
25% is merely, "part of his fortune is bar-gold."
I wonder if this is consistent with the way people actually use these phrases?
Matt B said,
August 4, 2010 @ 1:16 am
One thought that struck me in thinking about verification strategies for "most" and "more than half" is that they (to me) carry different commitments about precision. Felicitous use of "most" may not even require there to be a well-defined group. For instance, compare "Most people carry cell-phones" with "More than half of all people carry cell-phones". There's a sort of seamless accommodation about what group one is talking about (e.g. of course I mean wealthy citizens of developed countries, yada yada) that occurs with the first sentence that seems difficult to accomplish with the second (although, feel free to dispute these intuitions).
In the Lidz et al work I guess it would be hard to argue that respondents didn't share the experimenter's interpretation of the groups. I have to say that I thought it was pretty convincing evidence that people have an accessible interpretation of "most" == "more than half". On the other hand, it's notoriously tricky to relate verification to truth-conditions. Simply because a participant accepts a particular gloss on an utterance doesn't provide conclusive evidence that such an interpretation is part of an utterance's truth conditions.
On that last note, I'd be very interested to see how participants respond in this kind of paradigm to corner cases where all of the dots are blue. Would they affirm that "most dots are blue"? Given that the more widely assumed implicature is not [Most==greatest cardinality subset], but rather [most==not all], if they do in fact affirm it, then I think that this would bolster the case that they are providing their literal interpretation of "most" in this task. On the other hand, their failure to do so might weaken that claim and perhaps offer evidence for a competing claim that it is in fact "most"=="more than half" that is the implicature here, via a sort of pragmatic lenition of the conventional meaning of "most".
stephen said,
August 4, 2010 @ 7:46 am
I remember Orville Redenbacher's popcorn ads, in which he says, "Most every kernel pops." I'm sure he meant "almost all", and I'm sure the lawyers insisted on the "most" since somebody would sue if he or she found one unpopped kernel. But "most" is less noticeable than "almost all".
[(myl) The most in "most every" is not the adjective/quantifier most, but rather the adverb, which is basically an informal variant of almost. And I think the compositional meaning of "(al)most every" should be essentially the same as "almost all".]
Jerry Friedman said,
August 4, 2010 @ 12:58 pm
@myl: You said two of my speculations were possible, though improbable. Is there an implicature that my third speculation (that some people were answering correctly according to their definition of most but those answers were judged incorrect according to the experimenters' definition) was not possible? (If so, I can't relate it to the Gricean maxims, which was my first thought.)
Also, you thought that a sample of LL commenters would have given different results from a sample college students, but you thought my hypotheses, which would explain that disparity, were improbable. Do you have a more probable hypothesis?
The NSOED defines the relevant sense of most as "the greatest number of; the majority of; nearly all of." I can't tell whether the first gloss could be "plurality, whether a majority or not". I'm also not sure from the front matter whether the senses are in chronological order, though I suspect they are. If so, do we have any information on when the sense "nearly all of" arose? And your Gricean explanation sounds very plausible, but I wonder whether almost and the non-standard sense of most as almost could have had an influence.
Finding what meaning people have for a word must be very hard. I can imagine that you'd get different results from these questions:
Are most of the dots blue?
Is the following statement true? "Most of the dots are blue."
Would you make the following statement about the pattern of dots? "Most of the dots are blue."
Which of the following statements are true? Choose all that apply. 1. The majority of the dots are blue. 2. Most of the dots are blue. 3. Almost all of the dots are blue.
Mira Ariel said,
August 4, 2010 @ 3:12 pm
Hi,
Two points:
1. My semantic account for the upper bound on 'most' does not specify 'not all' (contra Larry Horn's presentation of my proposal). It just says that it's a proper subset (larger than 50%). In other words, it doesn't preclude 'all' is true in the world, although it does not include this value as one potentially asserted by the speaker. My main piece of evidence for the claim that 'most' does not (also) denote 100% is that subjects absolutely refuse to confirm that it does, even when the alternatives I presented them with were: 100%; 20%; 50%; 49%.
Of course, it can happen (but NOT very often, according to my subjects) that a speaker using 'most' will be taken as telling the truth even though 'all' is the case. But that's the same as telling the truth when we say 'I have a house' when in fact I have a house and an apartment.
2. I too found differences between 'most' and 'more than half'. First of all,unlike for 'most', quite a few subjects do accept 100% as a value for 'more than half', because indeed, that expression does not have a semantic upper bound. Another, pragmatic difference is that 'most' likes larger majorities than 'more than half' does.
Tim Hunter said,
August 5, 2010 @ 1:59 pm
In response to Jerry Friedman:
As far as I can recall, none of the subjects ever asked what was meant by 'most'.
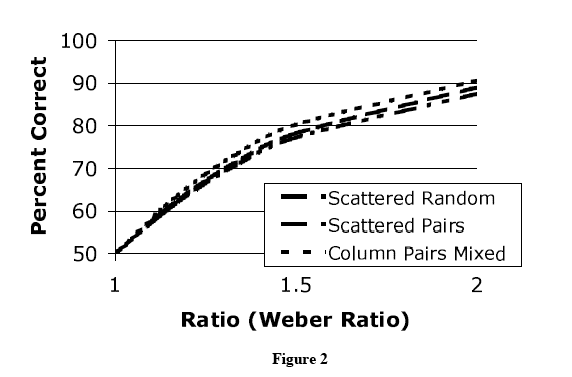
Certainly in cases such as 12 vs. 10, there was less agreement among responses than in cases of, say, 20 vs. 10. But the point is that the amount of disagreement at those "close" ratios is exactly the amount of disagreement predicted by the independently-established psychophysical model of how much disagreement one expects, at the various ratios, under the assumption that subjects were trying to compare the number of yellows and the number of blues. (In other words, this assumption plays a role in explaining the data; it doesn't play any role in shaping an explanandum.) The most thorough discussion of this point is in the Pietroski et al. M&L paper, pages 579-580. See also footnote 7 in the SALT paper.
Jerry Friedman said,
August 7, 2010 @ 12:13 am
@Mira Ariel: Thanks for the confirmation that some people outside Language Log associate most with bigger fractions than they associate with more than half.
@Tim Hunter: Thanks for your reply and for settling one of my speculations. It's interesting (to me) how I think of this differently after contact with one of the authors of the paper.
I'm trying to remember what I was like as a college student, and I'm thinking I might not have asked what you meant by most, contrary to what I implied above.
I'm sorry I missed that footnote in your paper. I'm not convinced by it yet, but if I make the graphs for the hypothesis that some of the subjects took most to mean a large majority, I'll probably see that they don't agree with the data.
Of course, if some of the subjects had understood most that way, it would have shown up as a lot of "No" answers when the ratio was close to 1, and you (plural) would have noticed that.