Towards a grammar of rhythm
« previous post | next post »
Hassan Munshi has been working on text setting in Arabic music. An important piece of the problem is how to represent the musical rhythms involved, and it's worth noting that (as with classical Greek, Latin, and Persian meters) the musical and poetic meters are founded on the same principles and have the same names. Hassan pointed me to an overview at MaqamWorld, which explains "Arabic Rhythmic Cycles":
Arabic music is composed over rhythmic cycles called iqa‘at (singular iqa‘), which are patterns of beats that repeat every measure. A composition can switch back and forth between many different iqa‘at. Each iqa‘ is defined using a prototypal measure and the two basic sounds: dum (bassy and sustained) and tak (dry and sharp).
The notated iqa‘ is meant to be a skeleton or a prototype for how to perform it. In practice, percussionists ornament an iqa‘ (flesh it out) with additional beats: dum-s, tak-s and whatever other sounds the instrument is able to produce. That ornamentation depends a lot on the genre of Arabic music, the desired arrangement aesthetic, the instrument itself, the size of the rhythm section, and on the percussionist’s personal style.
For each iqa', MaqsumWorld provides a notation of the basic pattern, some musical examples, and a "tabla demonstration" in which a drummer illustrates the process of "ornamentation". For Iqa' Maqsum, this is the basic pattern:

And this is the tabla demonstration by Faisal Zedan:
One simple way to explore the "ornamentation" is a tabular grid with one column for each minimal time-unit (here 32 to the bar), one row for each bar, and an indication in each cell of the presence of a dum or a tak:
# 01 02 03 04 | 05 06 07 08 | 09 10 11 12 | 13 14 15 16 | 17 18 19 20 | 21 22 23 24 | 25 26 27 28 | 29 30 31 32
01 d . . . t . . . . . . . t . . . d . . . . . . . t . . . . . . .
02 d . . . t . . . . . . . t . . . d . . . . . . . t . . . . . . .
03 d . . . t . . . t . . . t . . . d . . . t . . . t . . . t . t .
04 d . . . t . . . t . . . t . . . d . . . t . . . t . . . t . t .
05 d . . . t . . . t . t . t . . . d . . . t . t . t . . . t . t .
06 d . . . t . . . t . t . t . . . d . . . t . t . t . . . t . t .
07 d . . . t . . . t . t . t . . . d . . . t . t . t . . . t . t .
08 d . . . t . t . t . t . t . . . d . . . t . t . t . . . t . t .
09 d . . . t . t t t . t . t . . . d . t t t . t . t . t t t . t .
10 d . t . t . t t t . t . t . t . d . t t t . t . t . t t t . t .
11 d . t . t . t t t . t . t . t . d . t t t . t . t . t t t . t .
12 d . t . t . t t t . t . t . t . d . . . t . . . t . . . t . t .
13 d . . . t . . . t . . . t . . . d . . . t . . . t . . . t . t .
14 d . . . t . . . t . . . t . . . d . . . t . . . t . . . t . t .
15 d . . . t . . . t . . . t . . . d . . . t . . . t . . . t . t .
16 d . . . t . . . t . . . t . . . d . . . t . . . t . . . t . t .
17 d . . . t . . . t . . . t . . . d . . . t . . . t . . . t . t .
18 d . . . t . . . t . . . t . . . d . . . t . t . t . . . t . t .
19 d . . . t . t t t . t . t . t . d . t t t . t . t . t t t . t .
20 d . . . t . . . t . . . t . . . d . . . t . . . t . . . t . t .
21 d . . . t . . . t . . . t . . . d . t . t . t . . . . . . . . .
So "ornamentation" means that (at least in this sample)
- the two basic dums (positions 1 and 17)
and three basic taks (positions 5,13,25)
are always filled; - some positions (2,4,6,10,12,16,18,22,24,26,30,31)
are never filled; - and others (3,7,8,9,11,15,19,20,23,27,28,29,31)
are sometimes filled and sometimes not.
The "sometimes filled" positions have quite variable numbers of occurrences (in the completed bars 1 through 20), e.g. 3 in position 3, vs. 18 in positions 9 and 21.
If we sum up the number of drum strikes per column (in the completed bars), we get
# 01 02 03 04 | 05 06 07 08 | 09 10 11 12 | 13 14 15 16 | 17 18 19 20 | 21 22 23 24 | 25 26 27 28 | 29 30 31 32
20 0 3 0 20 0 6 5 18 0 9 0 20 0 4 0 20 0 4 4 18 0 9 0 20 0 4 4 18 0 18 0
Or graphically
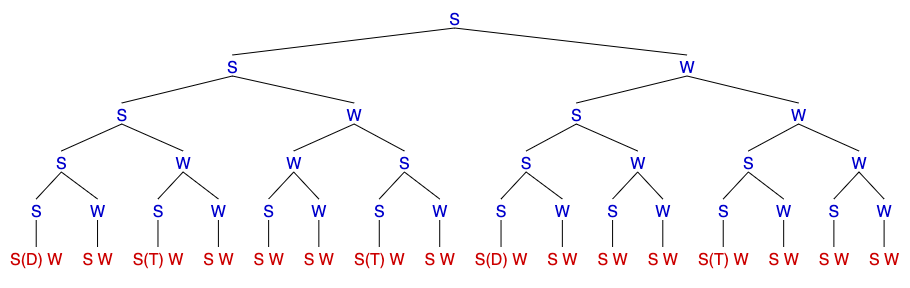
So given the 32-element metrical hierarchy at the level of a single measure of the maqsum pattern, it's almost enough to say that "strong is stronger than weak", assuming that the "syncopated" location of the second tak is represented something like this:
It's roughly true that no "weak" position can be filled unless the associated "strong" position is also filled — though obviously the choice is not made randomly position-by-position, since the overall level of "ornamentation" waxes and wanes in that sample, and no doubt in other performances as well. This points towards a stochastic grammar of this iqa', and presumably other iqa'at as well.
The Wikipedia article on "Rhythm in Arabic music" notes the similarities with Ottoman classical music, and the linked article notes that "Ottoman music traces its roots back to the music of the Hellenic and Persianate world." But we can see similar patterns in other musical traditions, including European ones.
 For example, let's take a look at the first 12 bars of the Gigue from Bach's French Suite #1. An image of the sheet music is on the right, and below is a performance on the piano by Glen Gould:
For example, let's take a look at the first 12 bars of the Gigue from Bach's French Suite #1. An image of the sheet music is on the right, and below is a performance on the piano by Glen Gould:
There are 32 32nd-note positions in each of the 12 bars. The work is polyphonic in three voices, and if we count how many note onsets occur in each position at each of the 32 possible times per bar (ignoring trills), with vertical-stroke characters separating the quarter note positions, we get
01 02 03 04 | 05 06 07 08 | 09 10 11 12 | 13 14 15 16 | 17 18 19 20 | 21 22 23 24 | 25 26 27 28 | 29 30 31 32 1 1 1 1 1 1 1 1 1 1 2 1 2 1 2 1 1 1 2 1 2 3 1 3 3 3 1 1 1 1 2 1 3 1 1 3 3 1 2 1 1 2 3 3 1 3 2 1 2 1 1 2 1 1 3 1 3 2 1 2 1 1 2 1 2 3 1 3 2 1 2 1 1 2 1 1 2 2 2 1 2 1 2 1 2 2 2 1 2 1 3 2 2 1 1 1 2 2 1 2 2 2 2 2 1 2 1 2 2 2 1 1 2 1 3 1 1 2 3 1 2 1 3 2 2 1 2 1 2 2 1 1 1 1 1 01 02 03 04 | 05 06 07 08 | 09 10 11 12 | 13 14 15 16 | 17 18 19 20 | 21 22 23 24 | 25 26 27 28 | 29 30 31 32
Summing the counts per position across the 12 bars, we get:
01 02 03 04 | 05 06 07 08 | 09 10 11 12 | 13 14 15 16 | 17 18 19 20 | 21 22 23 24 | 25 26 27 28 | 29 30 31 32
21 0 1 0 1 2 26 8 28 0 1 0 1 0 24 4 25 0 0 0 0 9 16 12 21 0 0 0 0 0 17 2
Or in graphical form:
To see more clearly what Wikipedia calls this piece's "distinctive strutting 'dotted' rhythm", we should move the upbeat (positions 31 and 32) to the front:
Again, there's more to say about how to represent the basic rhythm and generate its ornamentations, but a direction is clear.
Oddly, there does not seem to be much (if any) musicological work along these lines, though Ray Jackendoff has pointed me to a paper by Alice Singer, "The metrical structure of Macedonian dance" (Ethnomusicology 1974), which starts down a similar path. The author's research was cut short by her untimely demise, as described in Judith Irvine's introductory note:
Alice Singer, a graduate student in Anthropology, was preparing this paper for publication when she met her death in a road accident in July, 1973. In presenting the paper here, Ray Jackendoff and I are acting as her literary executors; both of us had discussed her work with her at some length. Although she had intended the paper as it stands here as only a working draft subject to further revision, we felt that the paper already holds interest and importance in its present form.
This study should have been only the beginning of a life-time's work on the interrelation of symbolic systems and the formal description of human behavior other than language. While Ms. Singer's special interest was dance — Macedonian dance in particular — she hoped to develop a mode of analysis more broadly applicable to other ethnic groups and other forms of behavior. Linguistic theory was to have been her methodological starting-point. We find this study a significant step toward her goal, and we deeply regret that such a promising intellectual career was cut short.
Google Scholar finds 51 citations for this paper — all are interesting, but (at least on a quick scan) none of them seems to go much further down the path towards a grammar of rhythm.



Steve Jones said,
November 13, 2021 @ 12:56 pm
Rhythm and metre, naturally, are major concerns of ethnomusicology, both for vocal and instrumental musics. Apart from the Middle East, Indian tala is much studied. Readers may like to consult AAWM journal
https://stephenjones.blog/2018/09/25/analyzing-world-music/
A personal fetish: aksak "limping" metres, common in Bulgaria and Turkey, and studied by Bartok; they are (or were…) also common in Uyghur music
https://stephenjones.blog/2018/12/06/taco-taco-taco-burrito/
[(myl) There's an enormous number of works, over the millennia, documenting and analyzing the meters of different traditions, genres, styles, and forms. What seems to be missing is any serious attempt to generate, constrain, or otherwise predict the variable patterns of "ornamentation" within any particular type of performance. (That is, which (detailed) patterns of rhythmic position-filling exist (or are more likely to exist) and which don't, as exemplified in a simple-minded way in the post above. If you know of any examples, please tell me about them!]
Steve Jones said,
November 13, 2021 @ 1:03 pm
As often, the wiki entry looks useful for a basic vocabulary
https://en.wikipedia.org/wiki/Metre_(music)
[(myl) Like everyone else who's studied musical and/or poetic meter, I'm familiar with the terminology. What seems to lacking, again, is any serious attempt to construct a system for generating (and assigning probabilities to) alternative instantiations of metrical patterns in musical composition and/or performance. It would also be nice to have a story about how those variable patterns evolve over the course of a particular piece or performance.]
wanda said,
November 13, 2021 @ 2:34 pm
This kind of looks like what some friends of mine in grad school were doing with the song of Bengalese finches. Unlike the widely studied zebra finch, the Bengalese finch doesn't have one fixed song. Rather, it has a set of "syllables" that it uses in varying orders according to higher-order, history-dependent patterns. My friends were trying to understand these song rules while recording from various areas of the bird's brains to understand how the birds made and carried out the decisions to sing one syllable instead of another.
[(myl) Yes, that's exactly the (general) sort of thing that's needed (and I think lacking) in cases like this. See e.g. "Finch linguistics", 7/13/2011, and "Modeling repetitive behavior", 5/15/2015.]
AntC said,
November 13, 2021 @ 4:12 pm
I'm wondering if the Natya Shastra text would include material on metrical subdivisions. The wiki says " centers around three themes – sound, rhythm and prosody applied to musical texts."
There's talk of the tonal divisions of the octave; metrical divisions for prosody should be right there.
AntC said,
November 13, 2021 @ 4:22 pm
aksak "limping" metres,
Yes, also a fetish of mine. Bach in particular made great use of asymmetric rhythms for emotional effect: 'Erbarme dich' in the Matthew Passion, the slow movement of the double violin concerto, Passacaglias and Chaconnes with slow 3-time. Also Beethoven's 'lumpy' rhythms in his late works: the String Quartets, the last Piano Sonata last movement Arietta (a C19th Chaconne).
Of course Bach would be the one to confound the whole idea: <a href="https://en.wikipedia.org/wiki/Prelude_and_Fugue_in_D_minor,_BWV_875" Fugue VI in D Minor of Book 2 of the 48: subject in triples, counter-subject in duples. There's an exquisite half-bar where they play against each other with "many accidentals" as wp puts it.
AntC said,
November 13, 2021 @ 4:31 pm
We should perhaps ask some jazz drummers who've transitioned to Rock. The three greatest are recently gone from us. If you listen to Charlie Watts, Ginger Baker or Jon Hiseman, it seems they never play exactly the same sub-rhythms in each repeat of the verse or chorus.
Dmitri said,
November 13, 2021 @ 4:40 pm
Interesting! I would imagine a lot of computer music folk have produced representations along these lines, but more for the purpose of creating music rather than analyzing it. There is, I think, a layer of subterranean "theory" there that is not easy to access; it is kind of an oral tradition.
I also would emphasize the cross-cutting and nearly even patterns formed by "dum" and "tak." You have DTTDT, with Ds and Ts nearly evenly distributed; then you have 12122 with 1s and 2s nearly evenly distributed (though differently from D and T), then you have D dividing the timespan into 2 and T dividing it nearly evenly into 3 (233). So everything is quasi-regular in an interestingly non-obvious and irregular way. This sort of near evenness strikes me as something that is found on specific metrical levels rather than all.
An interesting question is whether dum and tak collapse into a single conceptual level (as in your SW graph, which abstracts away from the distrinction) or whether there are two interacting streams here. Is it possible to see break out the dums and taks in the raw counts?
[(myl) Good question — The dums and taks are all labelled as such in the table as presented, so their patterns can certainly be explored separately. But the pattern of dumming is not at all mysterious, though, since all and only the dums are in positions 1 and 17. And the maqsum meter also makes taks obligatory in positions 5, 13, and 15 — the "ornamentation" action is all in the optional taks. My inclination would be to hope that a larger amount of data (about this and other meters, and by this and other performers) would reveal more about the underlying processes.]
AntC said,
November 13, 2021 @ 6:39 pm
<a href="https://www.wisdomlib.org/hinduism/book/the-natyashastra/d/doc210084.html"Natya Shastra Chapter XVI – Metrical Patterns (chandas). Is a catalogue of rhythms. Note especially section "The uneven and the semi-even metres" and ff.
And serendipity there's a pattern 'Lalitā': "the tip of the tongue taking a trip of three steps down the palate …". Or " O lady, hurriedly but gracefully moving the beautiful clothes and the delicate hands and having the beauty of a blooming lotus in the face you look charming to me after the fatigue of love’s sports."
Jacob Reed said,
November 15, 2021 @ 11:39 pm
There is in fact some musicological work along these lines, particularly by Graeme Boone (some of the charts in "Marking Mensural Time" may look very familiar to readers of this post!). Interestingly, Boone is also concerned with text-setting.
[(myl) Thanks! That's Boone, Graeme M. "Marking mensural time." Music Theory Spectrum 22, no. 1 (2000): 1-43. And here are a few dozen publications that reference it.]
Mark said,
November 15, 2021 @ 11:58 pm
Is there something buried in Schenker analysis that relates at all to this work?
Philip Taylor said,
November 16, 2021 @ 6:22 am
Knowing nothing of Graeme Boone but wanting to know more about his involvement with text-setting, I looked him up on the web and came to https://music.osu.edu/people/boone.44 . There I saw that he listed his education as having taken place at Harvard, University of California-Berkeley, and National Superior Conservatory of Music, Paris, but the last came as something of a shock — is it not normal to refer to a foreign institution by its "real" name rather than by a translation ? I would have expected Conservatoire National Supérieur de Musique et de Danse de Paris, and was genuinely shocked by Graeme's "National Superior Conservatory of Music, Paris", not only because of the use of translation but also because, in this context at least, I do not feel that the most felicitous translation of Supérieur is "Superior" — "Advanced" would feel more appropriate to me. What do others think ?
Mark Meckes said,
November 17, 2021 @ 9:31 am
Supporting myl's impression that a substantial "music theory for rhythm and meter" is lacking, I quote from Stephen C. Stone's 2019 textbook "Music Theory and Composition":
"Unfortunately, Western musicians have yet to develop a theory for rhythm as sophisticated as that for pitch. As a result, pitch will be emphasized over rhythm in this book. Do not let this deceive you, and do not ignore rhythmic issues. Rhythm is as important as pitch; we just lack the terminology to explain it well."