Language Log

« previous post |

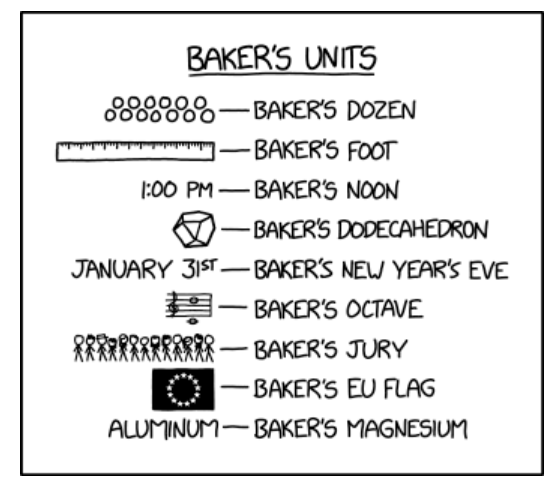
A recent xkcd:

Mouseover title: "169 is a baker's gross."

Everyone knows that a "baker's dozen" is 13, one more than a standard dozen, though Wikipedia told me a new story about its origin:

In England, when selling certain goods, bakers were obliged to sell goods by the dozen at a specific weight or quality (or a specific average weight). During this time, bakers who sold a dozen units that failed to meet this requirement could be penalized with a fine. Therefore, to avoid risking this penalty, some bakers included an extra unit to be sure the minimum weight was met, bringing the total to 13 units or what is now commonly known as a baker's dozen.

Randall's comic extends the generalization to other things whose normal count is 12: inches in a foot, hours from midnight to noon, faces of a dodecahedron, semitones in an octave, members of a jury, stars on the EU flag, the number of protons in magnesium's nucleus.

But as explainxkcd explains, Randall gets the musical example wrong:

In the 12-tone music systems, octaves contain 12 half-steps, also known as semitones (a half-step is the distance between adjacent notes, such as F and F#). A 'baker’s octave' would have 13 semitones (corresponding to a minor ninth) and cause problems in musical composition, as octaves (of the baker’s variety) would be dissonant, instead of being consonant. However, Randall's musical notation actually shows a major ninth, with fourteen semitones. If he wanted thirteen semitones, Randall could have used D♭ instead of D, or drawn a bass clef instead of a treble clef. Another way is to shift couple of notes up to make it E and F or one note down to make it B and C, both pairs are actually 13 semitones away from each other.

The "baker's octave" concept, without the error, resonates with a wonderful insight from Bill Sethares that's been on my to-blog list ever since I learned about it in a recent presentation ("Three eras of Pythagoreanism") by Dmitri Tymoczko.

A sketch of the musical math follows — see Tymoczko's slides and Sethares' book for the full story.  But you might want to start by skipping ahead to the musical examples, to decide whether the details are worth it.

Here's a quick explanation taken from three of Dmitri's slides:

• Consonance is not produced by numbers themselves.
• Instead, it arises through a process of dissonance minimization that depends on the structure of a sound, which in turn depends on the physics of the instrument involved.
• It is a minimum in a continuous space.
• A vibrating body produces partials according to its detailed physical construction.
• Consonance is produced when the partials of two sounds coincide (or are sufficiently distant so as not to interfere).
• Familiar instruments vibrate harmonically:
  –f, 2f, 3f, 4f, …
• The consonance of whole-number frequency ratios is due to the spectrum of the sound.
• Therefore, nonharmonic sounds would sound consonant at different, non-whole-number ratios.

In the material for his 1998 book Tuning, Timbre, Spectrum, Scale, Sethares observes that instruments with inharmonic partials, such as bells, are not only possible but common; and he works out what a 12-step scale based on an inharmonic "circle of fifths" would be like, in particular if the ratio of successive partials were 2.1 (= 13 semitones in a conventional 12-step scale — a baker's octave!) rather than 2.

As a clue about what that means, note that 2/1 partials take us step-by-step around the circle of fifths. If we start at 100 Hz, for example, the second overtone is at 3*100=300 Hz, which is one 2/1 octave up from 150 Hz, whose ratio of 3/2 relative to the starting point yields (the first) perfect fifth. See "Pavarotti and the crack to chaos" (1/9/2007) for one take on the rest of the story. Sethares works through the analogous scale construction for a different (2.1/1) overtone ratio.

Here's Sethares' video, illustrating how a bell-like instrument with 2.1/1 stretched partials sounds dissonant playing two notes separated by a traditional 2/1 octave, but consonant when the notes are in a 2.1/1 ratio:

Given the choice between an instrument with 2/1 (harmonic) and one with 2.1/1 (inharmonic) partials,  and the parallel choice between a scale based on harmonic (2/1) partials and one based on inharnomic (2.1/1) partials, there are then four possible variants of a given piece of music. (These examples are taken from the CD accompanying Sethares' book.)

1. Familiar scale (based on 2/1 partials) +
   Familiar instrument with harmonic (2/1) partials:
   
2. Familiar scale (based on 2/1 partials) +
   Instrument with stretched (2.1/1) partials:
   
3. Stretched scale (based on 2.1/1 partials) +
   Instrument with stretched (2.1/1) partials:
   
4. Stretched scale (based on 2.1/1 partials) +
   Familiar instrument with harmonic (2/1) partials:
   

May 25, 2025 @ 7:30 am · Filed by Mark Liberman under Linguistics in the comics

Permalink