Language Log

« previous post | next post »

Today's xkcd:

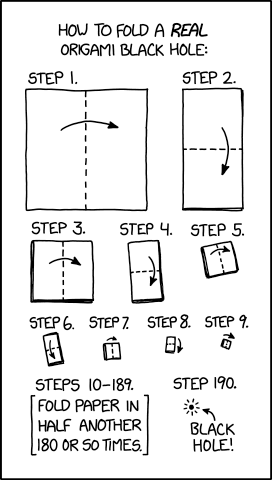
Mouseover title: "You may notice the first half of these instructions are similar to the instructions for a working nuclear fusion device. After the first few dozen steps, be sure to press down firmly and fold quickly to overcome fusion pressure."

No doubt you've considered the connection to the "Wheat and chessboard problem".

But 2^190 is a lot bigger than 2^64.

Physics-sophisticated readers are invited to explain why compressing the mass of a sheet of paper by (something like) that factor (allowing for the change along the way from 2 to 3 dimensions, fusion pressure, and whatever) would take us into black hole territory. I assume that Randall Munroe is sophisticated enough to have chosen the exponent appropriately, but it would be nice to see all the math, at least for an idealized folding regime.

The general idea is of course discussed in explainxkcd:

This comic is likely a reference to the Schwarzschild radius of a piece of paper. The Schwarzchild radius is a characteristic of every object that depends on the object's mass. If an object is compressed into the volume of a sphere with its characteristic Schwarzschild radius, then that object will become a black hole. (More specifically, it will become a Schwarzschild black hole.) As such, if a piece of paper were folded sufficiently many times so as to fit within its own Schwarzschild radius, it would become a black hole. However, this would require compressing the paper into a flat sheet at every step, otherwise the paper would have a thickness greatly exceeding its Schwarzschild radius.

If we assume standard kami origami paper with a side length of 15cm and a weight of 70 grams per square meter, we get a Schwarzschild radius of 2.339×10^-30 meters corresponding to a mass of 1.575 grams. It follows that, ignoring the paper's thickness, we would need to halve each side length -log2((2×2.339×10-30)/0.15)=94.69 times to fit each side length within the "Schwarzschild diameter" of the paper. Using the square folding technique in the comic, this would take approximately 95*2=190 steps to complete, the exact number given in the comic. Note that the radius of the resulting black hole is 15 orders of magnitude smaller than the charge radius of a proton.

Aside from the practical problems involved accomplishing that many folds, the explaination notes that "prior to reaching any creation of a black hole, the pressures generated by the resulting fusion of its atoms must be overcome. Electron and neutron degeneracy pressure would also have to be overcome".

January 4, 2025 @ 1:41 pm · Filed by Mark Liberman under Linguistics in the comics

Permalink