Talking is like living
« previous post | next post »
…and ending a sentence is like dying.
What do I mean by this weird and even creepy statement?
Short answer: Your probability of continuing to live is not constant, but decreases exponentially as you get older. (Actuaries know this as the Gompertz-Makeham Law of Mortality, usually expressed in terms of your probability of dying.)
A generative model of this type, on a shorter time scale, is a surprisingly good fit to the distributions of speech- and silence-segment durations in speech, and also to the distribution of sentence lengths in text. A shockingly good fit, in most cases.
Long answer: See below, if you have the patience…
This all started with birdsong. Zebra Finch "song bouts" are sequences of "motifs", each of which is a (pretty much fixed) sequence of "syllables". (See "Finch Linguistics", 7/13/2011.) The number of motifs in a song bout varies, and so it seems reasonable to model the process as a two-state markov process, where the song bout is just one motif after another, with a fixed probability of stopping, Pstop , and a complementary probability (1-Pstop) of continuing to sing:
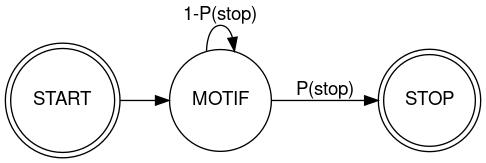
But in the cited post I showed that the (empirical) continuation probability is not fixed, but rather declines exponentially from one motif repetition to the next. This makes sense — in effect the bird is getting tired — but it does mean that the bird's "grammar" is not Finite State.
In "Modeling repetitive behavior", 5/15/2015, I observed that as a consequence
In modeling the structure of simple repetitive behavior, considerations from (traditional) formal language theory can obscure rather than clarify the issues. These threats to insight include the levels of the Chomsky-Schützenberger hierarchy, the "recursion" controversy, and so on.
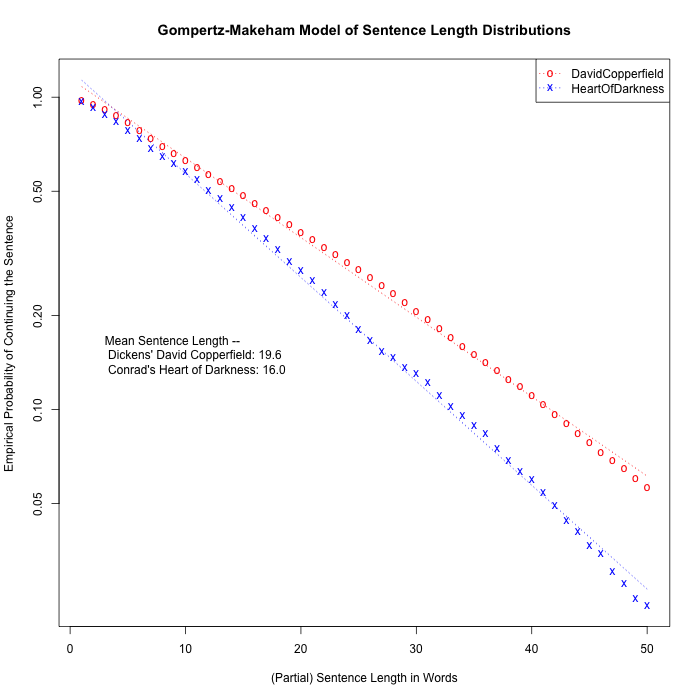
In contrast, in "Markov's Heart of Darkness", 7/18/2011, I found that paragraph lengths in Joseph Conrad's Heart of Darkness are (curiously) well modeled as a two-state Markov process:
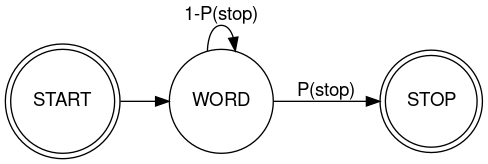
(Though as we'll see below, empirical sentence-continuation probabilities in Heart of Darkness again look like a decaying exponential.)
In "Audiobooks as birdsong",7/10/2018, I applied the same idea to the distribution of speech-segment durations in (a locally re-aligned version of) the LibriSpeech corpus. Our local version has 5,831 chapters from 2,484 speakers, and a total duration of 1570:39:50.82, with 2,086,576 speech segments. And I found that the probability of continuing to talk, like the bird's probability of continuing to sing, was again very well modeled by a declining exponential, showing pretty much a straight line on a log scale.
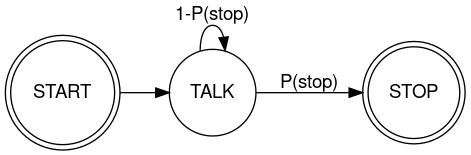
In response to that post, Dean Foster clued me in to the relevance of the Gompertz-Makeham Law of Mortality.
More recently, since we've been using speech-segment and silence-segment durations as features in clinical applications, I did a little exploration of such exponential models of speech-segment distributions in conversational telephone speech — see "The dynamics of talk maps", 9/30/2022, and "More on conversational dynamics", 10/2/2022.
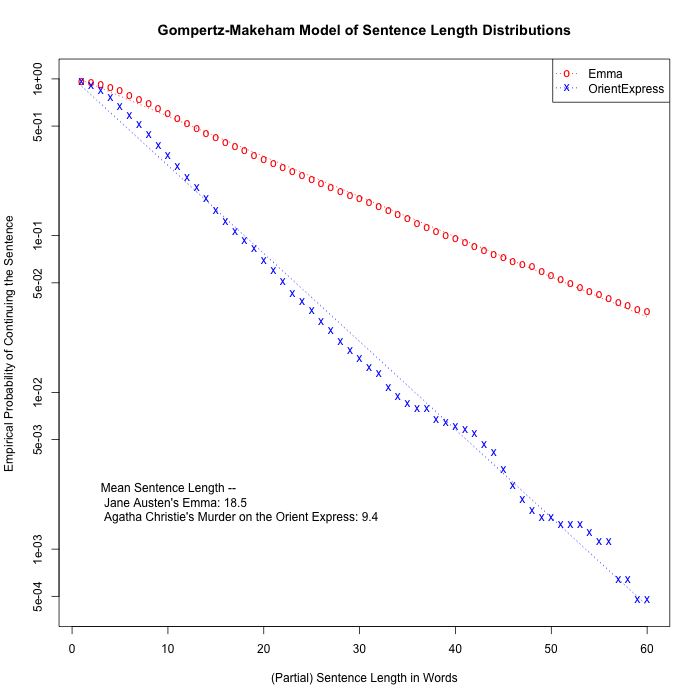
And just for fun, I thought I'd look at sentence-length distributions in a sample of books that I'd already divided into sentences (See e.g. "Historical trends in English sentence length and complexity" for the earlier goals…)
Here are the empirical probabilities of continuing, after each of the first 60 words in the 8,582 sentences of Jane Austen's novel Emma:
[1] 0.97051969 0.95374039 0.92880447 0.88767187 0.83989746 0.79025868 [7] 0.74096947 0.69436029 0.64751806 0.60382195 0.56012584 0.51794454 [13] 0.48391983 0.45222559 0.42123048 0.39419716 0.37100909 0.34921930 [19] 0.32614775 0.30540667 0.28897693 0.27079935 0.25553484 0.24166861 [25] 0.22791890 0.21428571 0.20251690 0.19074808 0.18072710 0.17187136 [31] 0.16208343 0.15346073 0.14530412 0.13726404 0.12887439 0.12013517 [37] 0.11360988 0.10696807 0.10102540 0.09601491 0.09053834 0.08552785 [43] 0.08063388 0.07632254 0.07247728 0.06898159 0.06560242 0.06350501 [49] 0.05954323 0.05593102 0.05278490 0.04987182 0.04660918 0.04392915 [55] 0.04206479 0.03950128 0.03728735 0.03588907 0.03390818 0.03262643
And here are the same numbers for the 6,241 sentences in Agatha Christie's Murder on the Orient Express:
[1] 0.9604230091 0.9120333280 0.8460182663 0.7641403621 0.6672007691 [6] 0.5842012498 0.5093734978 0.4419163596 0.3775036052 0.3249479250 [11] 0.2783207819 0.2339368691 0.2033327992 0.1728889601 0.1454895049 [16] 0.1241788175 0.1070341291 0.0926133632 0.0828392886 0.0700208300 [21] 0.0597660631 0.0511136036 0.0429418362 0.0381349143 0.0331677616 [26] 0.0285210703 0.0249959942 0.0211504567 0.0184265342 0.0165037654 [31] 0.0144207659 0.0131389200 0.0107354591 0.0094536132 0.0084922288 [36] 0.0078513059 0.0078513059 0.0067296908 0.0064092293 0.0060887678 [41] 0.0057683064 0.0054478449 0.0046466912 0.0041659990 0.0032046146 [46] 0.0025636917 0.0020829995 0.0017625381 0.0016023073 0.0016023073 [51] 0.0014420766 0.0014420766 0.0014420766 0.0012818459 0.0011216151 [56] 0.0011216151 0.0006409229 0.0006409229 0.0004806922 0.0004806922
In both cases, the numbers are not only decreasing monotonically, but are eerily well fitted by an exponential:
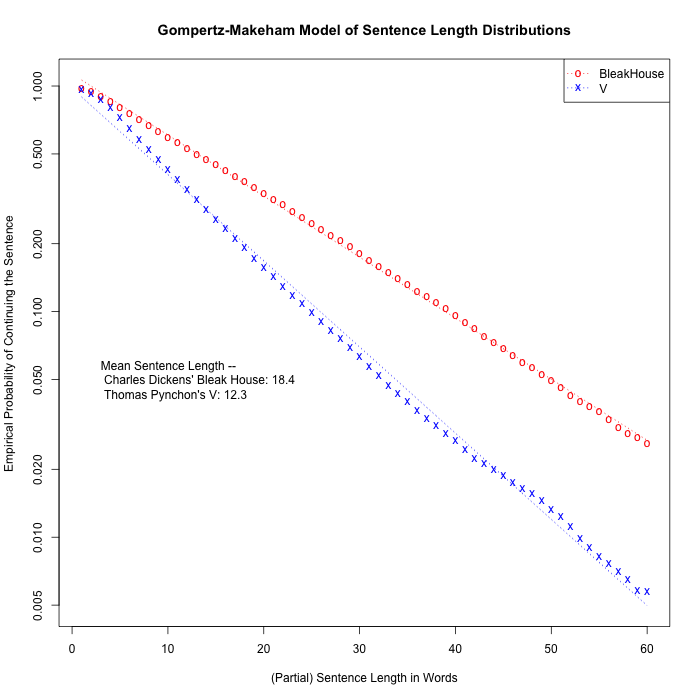
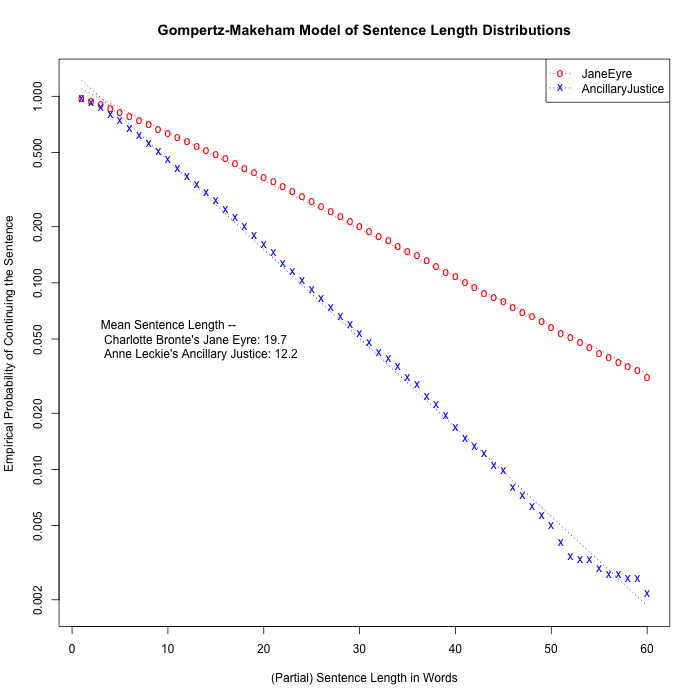
A few plots comparing other books — all of which show the same pattern, though the slopes (aligning with the mean sentence lengths) can be different:
Including one showing the fit for Heart of Darkness, which is pretty good despite the relatively small number of sentences (2,374):
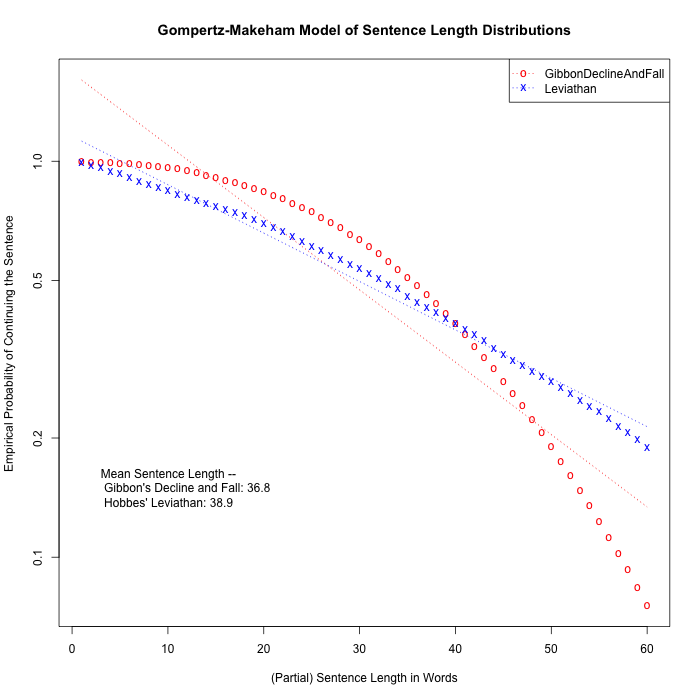
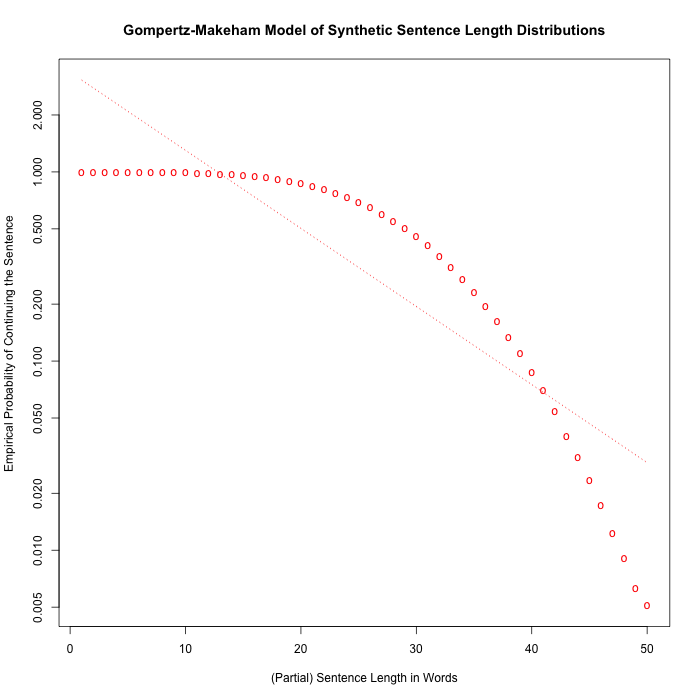
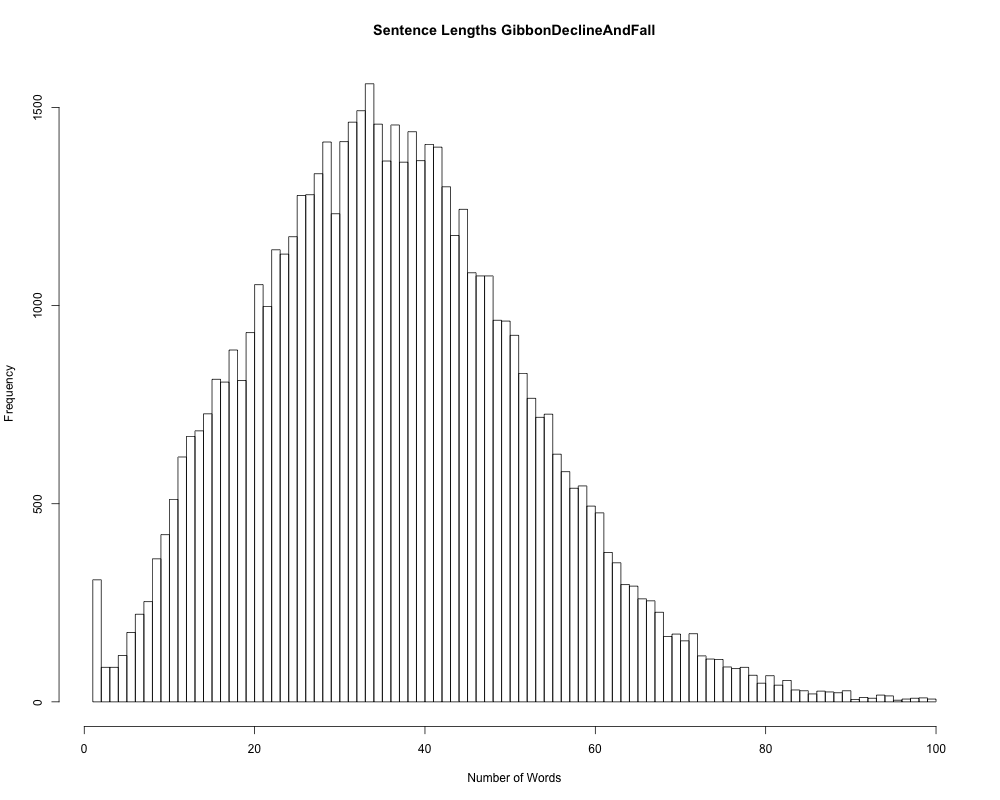
Just to show that it ain't necessarily so — for some reason, Gibbon's Decline and Fall of the Roman Empire seems to work differently, though Hobbes' Leviathan is fairly Gompertzian:
I'm glad, because this helps make it clear that not every possible distribution of sentence lengths necessarily shows the Gompertz-Makeham patterns. (Assuming that the Gibbon result is not the result of a bug in my sentence-division program…)
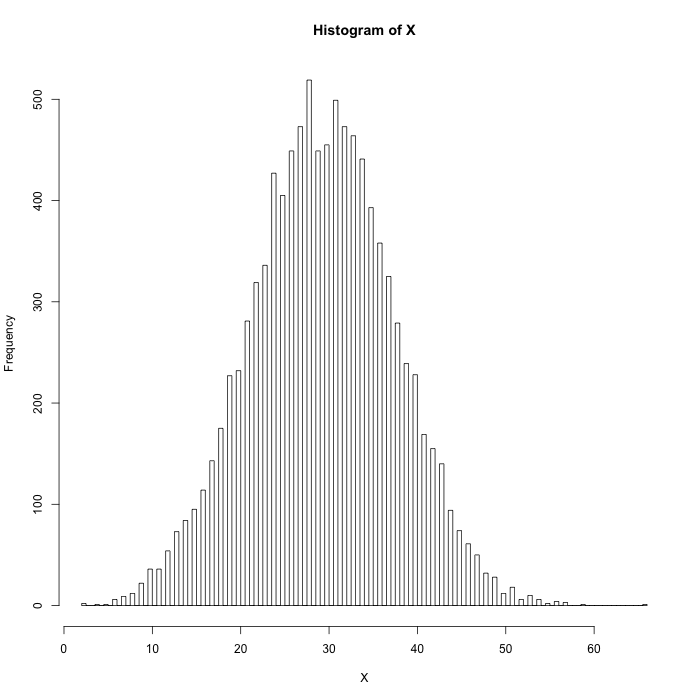
10,000 sentences with normally-distributed random lengths (mean 30, sd 8) show a similar lack of exponential fit:
The histograms of sentence lengths in Gibbon and in the synthetic set:
Why do sentences in most books work like mortality statistics? Some kind of Central Limit Theorem for recursive Merge? Perhaps someone will explain it to us in the comments.
LW said,
October 11, 2022 @ 3:15 pm
i'm afraid this comment is going to display my ignorance of pretty much anything related to statistics, but: would you mind explaining the meaning of "1-P(stop)"? i would have thought, if probability is measured from 0 to 1, that 1-P(x) would result in a negative probability – of course that can't be the case, but i don't know why.
LW said,
October 11, 2022 @ 3:16 pm
oh, never mind: i see that 1-P(x) is simply the inverse of the probability of P(x) and clearly can't be negative. sorry for the useless comment spam.
Y said,
October 11, 2022 @ 6:44 pm
Suppose that adding a word to a sentence depends on keeping the rest of it in memory, which becomes harder the longer the sentence is. What sort of empirical models of short-term memory exist, in particular for hierarchical structures such as are used in natural language?
Mark said,
October 11, 2022 @ 8:27 pm
"the (empirical) stopping probability is not fixed, but rather declines exponentially from one motif repetition to the next" — you mean the continuation probability.
[(myl) Indeed. Fixed now — thanks.]
Jerry Packard said,
October 12, 2022 @ 11:18 am
Following what Y said said, memory stack crunch could explain it if the producer had to keep the previous production in memory while the current production is being produced, which doesn't seem likely in the case of written texts such as books. Y is right in asking about models of short-term memory, though, as investigators like Brian McElree examine just those factors.
Central Limit Theorem doesn't seem to me to be a good explanation, as CLM talks about production probability independent of a, e.g., behavioral, component (e.g., fatigue).
[(myl) My "central limit theorem" suggestion was just a joke — but a "memory stack crunch" theory implies that short-term memory has been gradually declining among English-language writers for three centuries. Which is not very plausible.]
I have another idea based on my pet project: the distribution of old/new information. It is well known that in language production, new information tends to follow old. So the increasing likelihood of shorter utterances (motifs) could be because there is an increasing (over time) desire to produce new information that is of limited length, as an aid to hearer/reader comprehension. Hypothesis: writers/speakers tend to limit length of new information so as not to overwhelm the reader/listener. Old info aids the reader, because it sets the context.
[(myl) The general idea is plausible — but
(1) why would that lead to such an exact exponential decay in continuation probability for a given book, with slopes differing widely among books?
(2) why would the effect have been changing gradually but systematically over the past few centuries?
]
Mark Dow said,
October 12, 2022 @ 3:19 pm
Emily Dickinson also considered the co-incidence of sentence (double meaning) and lifespan, with a Calvinist slant: see "I read my sentence steadily…" Complete text at: https://en.wikisource.org/wiki/I_read_my_sentence_%E2%80%94_steadily_%E2%80%94
AntC said,
October 12, 2022 @ 7:49 pm
Although single-word or two-word sentences are not unknown in informal speech, I think a literary author would regard them as poor style. Then am I seeing a small 'bump' in some of those graphs below the 10-word mark? That is, if you've got to word two already, it's _more_ likely there'll be at least eight or nine.
Is there a difference in the sentences that are quoted speech vs reported speech vs narrative?
I'd expect the 'bump' to be more noticeable in the Gibbon or Hobbes. Or is that smudged by the scaling?
D.O. said,
October 13, 2022 @ 12:28 am
Theoretically, "half-normal" distribution should be just the ticket. Take normal distribution with central value 0 and count only positive outcomes (or take absolute value of all outcomes). Probability of n+1 words conditional on n words will be P(n+1)/P(n) ~ exp(-(2n+1)/(2s^2)). Maybe constructing sentences is both addition and subtraction process in a random walk fashion?
D.O. said,
October 13, 2022 @ 1:19 am
Sorry, I maybe misunderstood what "empirical probability of continuing" means. Does empirical probability of continuing after, say, 30 words in Emma, which in the table is 0.17187, means that there are about 0.17187*8582 = 1475 sentences of the length 31 and greater? If so, it is not Gompertz law, it is the usual geometric distribution with p(n) = (1-a)*a^(n-1) (assuming there are no sentences of length zero, interesting idea though it is) and probability of the tail P(>n) = a^n.
Manage Business said,
October 13, 2022 @ 6:35 am
It's hard to read these graphs, but thanks for the explanation. I think I understand the probability of continuing isn't really a hard concept to grasp. But how did Cinderella ever find the frozen carrot?
SP said,
October 13, 2022 @ 6:56 am
Could you add a sentence-length histogram for one of the cases where the Gompertz-Makeham model does fit well? Maybe it should be obvious what it looks like, but it isn't to me.
Thomas Shaw said,
October 13, 2022 @ 10:13 am
D.O. said:
> Does empirical probability of continuing after, say, 30 words in Emma, which in the table is 0.17187, means that there are about 0.17187*8582 = 1475 sentences of the length 31 and greater?
I don't think this is right. I think the probability of continuing should be interpreted as the conditional probability, conditioned on the sentence being at least 30 words, in other words: (# sentences > 30 words)/(# sentences >= 30 words).
D.O. said,
October 13, 2022 @ 12:04 pm
Thomas Shaw, that was my first idea as well. But then I multiplied all such factors for Emma and got 10^-46, which clearly cannot be.
Thomas Shaw said,
October 13, 2022 @ 12:43 pm
You make a good point. I also notice that the results seem to be integer multiples of 1/(total number of sentences in the work). So I agree it seems like what is actually being calculated here is (# of sentences > n words)/(# of sentences). I still think that what is being discussed earlier in the post is like what I wrote in my previous comment, though. Maybe @myl can clarify?
Michael Lyon said,
October 17, 2022 @ 6:00 am
I think I get the same as Thomas Shaw (for 'Emma'); on that presumption, if I calculate the conditional probabilities of sentence continuation, these seem to settle down to a constant-looking rate rate of around 0.94 after 7 words or so; before 7 words sentence continuation rates are somewhat higher. That would look like a model of exponential decay applying after that initial length, with no special longer sentence effect beyond that threshold. But for the very shortest sentences, it would seem to imply that these are un-preferred: perhaps that words need a certain minimum amount of combination in order to convey useful meaning.