A different perspective on family name distributions
« previous post | next post »
Michael Ramscar, "The empirical structure of word frequency distributions", arXiv 1/9/2020:
The frequencies at which individual words occur across languages follow power law distributions, a pattern of findings known as Zipf's law. A vast literature argues over whether this serves to optimize the efficiency of human communication, however this claim is necessarily post hoc, and it has been suggested that Zipf's law may in fact describe mixtures of other distributions. From this perspective, recent findings that Sinosphere first (family) names are geometrically distributed are notable, because this is actually consistent with information theoretic predictions regarding optimal coding. First names form natural communicative distributions in most languages, and I show that when analyzed in relation to the communities in which they are used, first name distributions across a diverse set of languages are both geometric and, historically, remarkably similar, with power law distributions only emerging when empirical distributions are aggregated. I then show this pattern of findings replicates in communicative distributions of English nouns and verbs. These results indicate that if lexical distributions support efficient communication, they do so because their functional structures directly satisfy the constraints described by information theory, and not because of Zipf's law. Understanding the function of these information structures is likely to be key to explaining humankind's remarkable communicative capacities.
A telling figure (read the paper for context):
And another one:
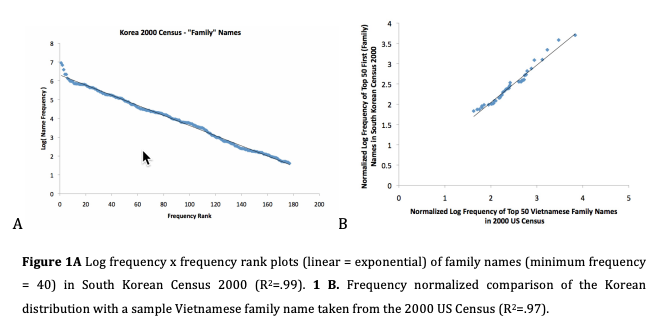
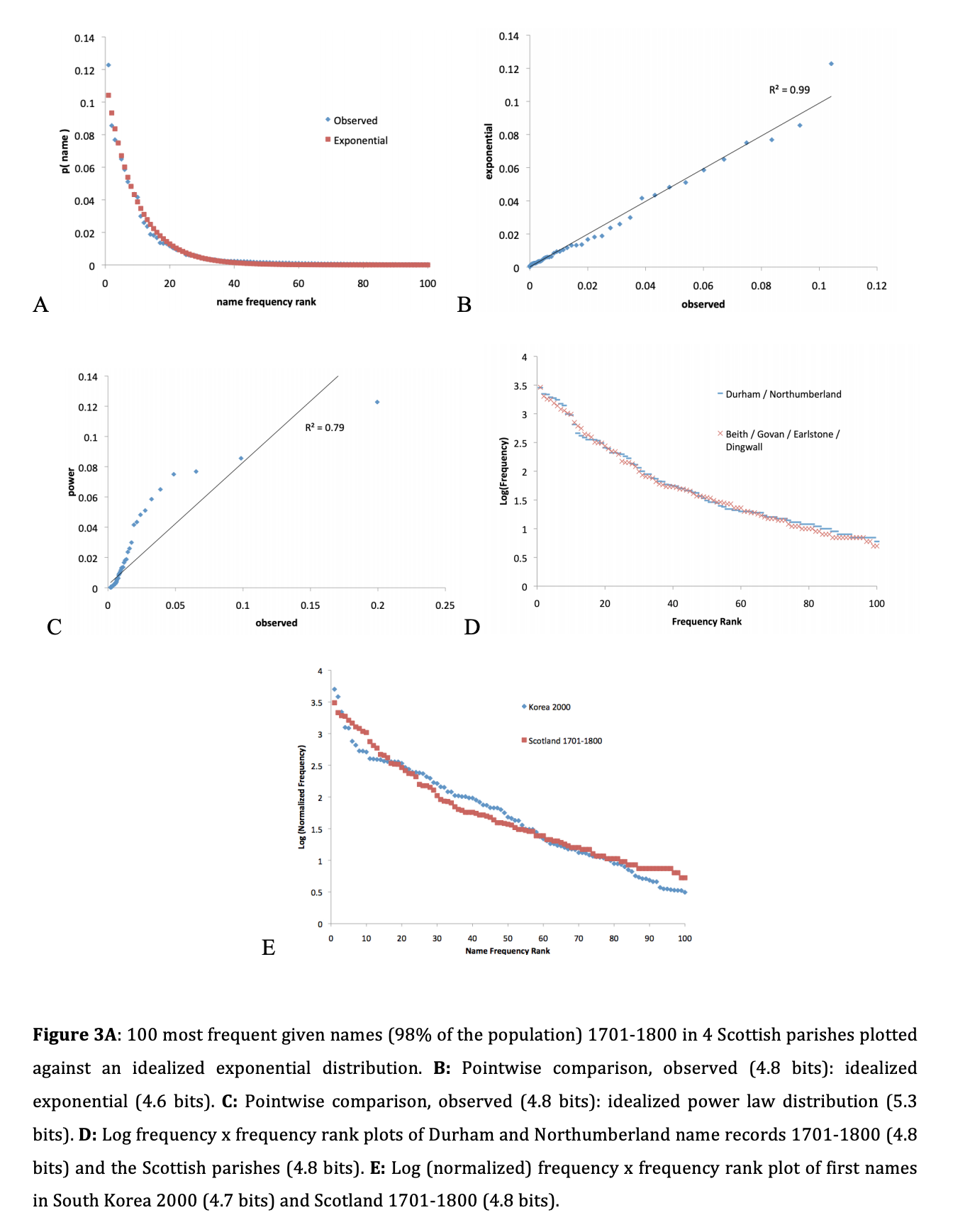
Rick Rubenstein said,
January 20, 2020 @ 12:10 am
I'm a bit confused. How could the distribution of family names be due to "the constraints described by information theory" if those names are clearly a product of (some combination of) historical happenstance and the differential reproductive success of various family lineages? What exactly is the proposed cause and effect here? Clearly people don't "choose" their family names with an aim to improve communication. I think I must be missing something.
AG said,
January 20, 2020 @ 3:51 am
I'm confused as well, by the article in general (probably just due to my own ignorance of "power law distribution" etc.), but particularly by the conclusion's thing about Charles Darwin and Charles Dickens both being "Charles D.". Are personal names in China a lot more unique than family names? Is that something that this paper proves somehow?
Andrew Usher said,
January 20, 2020 @ 9:37 pm
This is what I would call stream-of-consciousness science that ought to not have been presented in that form, even apart from substantive problems that would remain.
The author appears to be convinced that 'Sinosphere' family names should map to Western given names because they occur first in order, but this ignores the fact that word order does not determine grammatical structure. It does not seem likely that their family names fall into the same mental box as our first names, and would require stronger evidence than anything in his paper.
k_over_hbarc at yahoo.com
AntC said,
January 20, 2020 @ 11:47 pm
I'm also confused. Is this post some sort of rejoinder to Professor Mair's on the Vietnamese family name Nguyen?
Does Zipf's law predict (or is it consistent with) two-fifths of a population having the same first (family) name? (Or the preponderance of Kim in Korea?) As Prof Mair's post points out, this is the opposite of useful for purposes of communication.
Andrew Usher said,
January 21, 2020 @ 10:37 pm
Zipf's law can't say what the proportion of #1 will be. Of course it is bad for communication to have a very high proportion, but the author of this bogus paper surely didn't even consider it.