Jill Abramson's voice: difference tones?
« previous post | next post »
John Kingston's comment on "Jill Abramson's voice" (10/18/2010) suggests that what's going on in her final low-pitched syllables is a kind of difference tone, or "beat":
I wonder if the modulation is a rather extreme form of tremolo, which is a regular variation in level. Now, giving it a name doesn't explain how she does it, but in two-reed instruments it's a product of tuning them slightly differently, and as a result producing beats. The question then becomes how this could be produced with vocal fold vibration, in particular, how the vocal folds could be caused to vibrate at two frequencies at once about 25 Hz apart. I haven't got a clue, but suspect that it is related to the low F0 she produces at the same time.
The oscillation of the vocal folds is a physically complex phenomenon, and both in numerical simulations and in real observations, two or more different periodicities can sometimes be observed (though I have no idea whether that's what's behind the observed low-frequency modulation in Ms. Abramson's voice).
From a clinical perspective, my understanding is that this is what diplophonia is. See e.g. Shigeru Kiritani, Hajime Hirose and Hiroshi Imagawa, "Vocal Fold Vibration and the Speech Waveform in Diplophonia", Ann. Bull. RILP, 1991, who discuss different frequencies of vibration in the left and right vocal folds. I believe that similar differences can sometimes occur between the front and back or top and bottom portions, though obviously these subparts are less well differentiated than the left and right portions are.
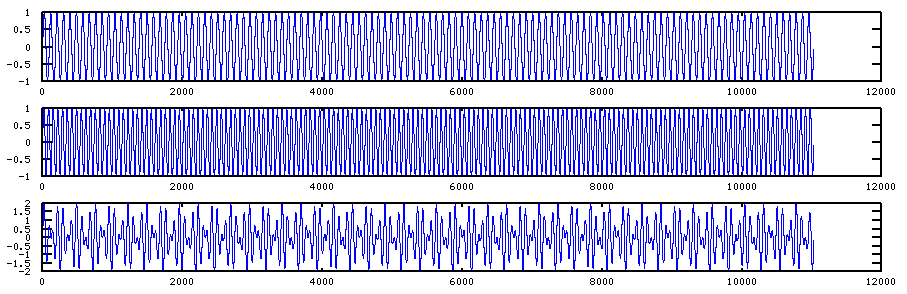
From a certain point of view, the formation of beats, at a frequency corresponding to the difference of the frequencies of two summed sinusoids, is mathematically trivial, as this fragment of Matlab (or Octave) code illustrates. We create two sine waves, one at 120 Hz and the other 165 Hz, and a third that's simply the sum of the two:
x = 2*pi*(0:11024)/11025;
y1 = sin(120*x); y2 = sin(165*x); y3 = y1+y2;
subplot(3,1,1); plot(y1);
subplot(3,1,2); plot(y2);
subplot(3,1,3); plot(y3);
wavwrite(y1',11025,"Beat45a.wav");
wavwrite(y2',11025,"Beat45b.wav");
wavwrite(y3',11025,"Beat45c.wav");
This produces the following plot of the three waveforms, in which the summed signal shows the apparent modulation of amplitude at a frequency corresponding to the difference of the two sine waves that make it up:
And the corresponding audio clips (recoded as mp3 with onset and offset fades to avoid clicks):
| y1 (120 Hz): | |
| y2 (165 Hz): | |
| y1+y2: |
We can also take the trigonometry in the other direction, so that (as Wikipedia explains in the article on Amplitude Modulation), when we modulate the amplitude of a carrier c(t) with a lower-frequency signal m(t),
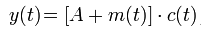
y(t) can be trigonometrically manipulated into the following equivalent form:
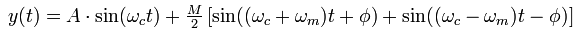
Therefore, the modulated signal has three components, a carrier wave and two sinusoidal waves (known as sidebands) whose frequencies are slightly above and below ωc.
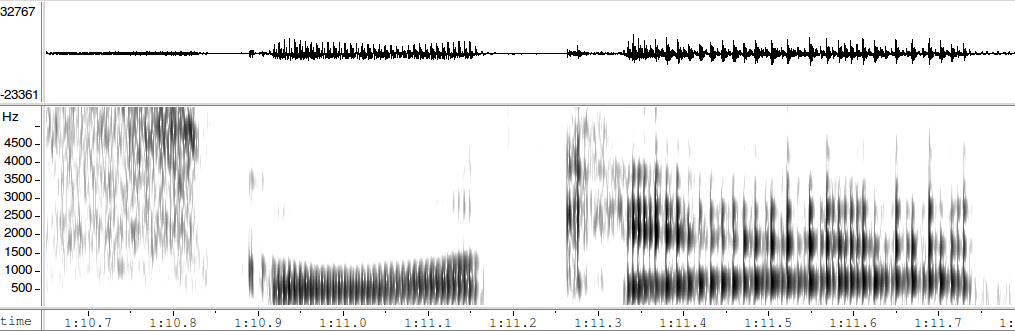
The corresponding vocal-tract physics is somewhat less trivial; and that lack of triviality extends to explaining how (what is probably) the same phenomenon can sometimes result not in a regular low-frequency modulation but in "vocal fry" — a state of chaotic vibration without stable periodicity — as was illustrated in my earlier post in the last syllable of Ms. Abramson's pronunciation of the word "schoolkid":
Jerry Friedman said,
October 21, 2011 @ 12:27 pm
If Ms. Abramson's voice has a 25Hz difference tone at some times, shouldn't one be able to find the two tones that are 25 Hz apart? And shouldn't those signals be fairly clear, considering how clear the 25 Hz modulation is?
[(myl) Maybe. But it's not so simple. My example used two sine waves that are 45 Hz apart (so that the difference tone is easy to hear). In her case — and in real-world cases in general — if there are two different physical oscillations being added up, each of them has a complex overtone series and a more-or-less 1/F spectrum; and their frequencies are not entirely constant; and they are probably tied together in some non-linear way. So the picture may not be so clear…]
Eric P Smith said,
October 21, 2011 @ 9:54 pm
I’m sorry to spoil the party, but I’m fairly sure that, while Jill Abramson certainly has an unusual voice, the apparent amplitude modulation in the spectrograms is an artefact of the spectral analysis software.
My suspicions were first aroused when I measured for myself the apparent amplitude modulation rate in the last syllable of the first spectrogram of Mark’s post of October 18, and I made it 16 beats per second (8 beats between 3.0 seconds and 3.5 seconds). Now, an amplitude modulation rate of 16 beats per second should be just audible as a fast vibrato, and I couldn’t hear it. So I downloaded the sound clip and played it at half speed: still no vibrato. Quarter speed: still no vibrato. Next I opened the sound clip in Praat, and there was no trace of the apparent amplitude modulation. However, I was able to reproduce it by changing the Praat settings for the number of time steps along the time window for which Praat has to compute the spectrum. I reproduced the 16 beats per second by adjusting the number of time steps so that the sampling rate was 300 steps per second. The 16 beats per second then arise as the difference between the sampling rate of 300Hz and the speaker’s second harmonic of 284Hz (F0 = 142Hz). Experimenting with other nearby sample rates confirmed the arithmetical relationship. Asking Pratt to display the intensity shows that the intensity varies in phase with the visible beats, but only very slightly. Using a sampling rate that is not close to any multiple of F0 destroys the apparent periodicity of the intensity.
[(myl) I worried, when I made the original post, that this might be a moire effect of the type that you're talking about. By trying a variety of different analysis window lengths and window advancement steps; and a variety of different display sizes, and also by looking at waveforms as well as spectrograms, I convinced myself that it was not an analysis artefact. Of course, I might have been wrong.
I don't have time for futher analysis today, but I'll take another look later this weekend.]
D.O. said,
October 22, 2011 @ 12:43 am
@Eric P Smith. Original spectrogram goes up to 5kHz, which assumes sampling rate of at least 10kHz, no?
maidhc said,
October 22, 2011 @ 2:53 am
Is "two-reed instrument" referring to an accordion? In that case, a tremolo or vibrato is produced by tuning two reeds at slightly different frequencies, creating a beat frequency. Tremolo is the correct term, meaning a variation in amplitude, while vibrato is a variation in pitch.
The difference is usually measured in cents, where one cent is 1/100th of a semitone, a semitone being the ratio of the twelfth root of two. A "wet tuned" accordion could have the reeds as much as 20 cents apart. Here's a link if you want to follow up on this approach: http://www.accordionpage.com/wetdry.html
Whether a person can have the two folds of their vocal tract vibrating at two different frequencies is out of my area of knowledge, and the supplied link is not working. Frequency of vibration would be determined by air pressure and muscle tension, would it not?
If you sample at 300 Hz, then the maximum frequency that can be reproduced is 150 Hz. Any higher frequency would be reflected back into the range 0-150 Hz. I'm not sure I see how selecting the sampling frequency to produce a certain result shows anything, but perhaps I am missing something. I would like to see a more detailed explanation.
Unfortunately my sound driver is malfunctioning at present, so I'm not able to listen to the examples.
Eric P Smith said,
October 22, 2011 @ 4:58 am
Sorry, my use of the term “sampling rate” was confused and confusing.
As you say, the original waveform must have had a sampling rate of at least 10000 Hz. The waveform on which I did my experiments had a sampling rate of 44100Hz. The 300 steps per second that I referred to in my last comment is the number of time steps per second in the spectrogram: the number of points along the time window for which the software has to compute the spectrum for every second of speech.
Indeed, looking more closely at the spectrograms in Mark’s post of 18 October, the situation becomes totally clear. Take the first picture in that post, the spectrogram of the utterance “it means the world to me uh”, the one with the time scale along the bottom. Click to embiggen, and you see the spectrogram as originally generated by the spectrogram software. Right-click it, and click Save Picture As. Save the picture, and view it in any image editor (eg Photoshop). Horizontally, there are 300 pixels per second of time as shown by the time scale along the bottom. Each pixel horizontally is one time frame for which the software computed the spectrum. This confirms my suspicion that the software used 300 steps per second, and explains why I had to use 300 steps per second to replicate the effect. Between 3.0 seconds and 3.5 seconds, there are 8 beats visible, which is 16 beats per second. That is the difference between the 300 steps per second used by the spectrogram software, and the speaker’s second harmonic of 284Hz.
Now compare that, carefully, with the second picture in the same post, which shows the tail-end of the utterance, “to me uh”. It will not emibiggen: it is displayed at the size originally generated by the spectrogram software. But the scale is slightly larger than the embiggened first picture. I can’t measure the difference precisely as there is no time scale along the bottom of the second picture, but by displaying the two images in an image editor and comparing salient features of the spectrograms I conclude that in the second image there are about 308 pixels per second of time, as against the 300 of the first image. Again, each pixel horizontally is one time frame for which the software computed the spectrum. However – and this is the clincher – between 3.0 and 3.5 seconds there are 12 beats in the second picture, as against 8 in the first. You can see the difference in your browser if you scroll so that the second picture is at the very bottom of the screen, and then embiggen the first picture, and you can see both pictures on the screen at the same time. Although the second picture is on a slightly larger scale than the first picture, the beats in the second picture are plainly closer together than in the first picture. The arithmetic of the second picture is: 308 steps per second, less the 284Hz of the speaker’s second harmonic, gives 24 beats per second.
Imo, that shows decisively that the apparent beats are an artefact of the spectrogram software.
Eric P Smith said,
October 22, 2011 @ 6:19 am
I might add that, while I have seen artefacts like this in spectrograms before, they appear so clearly in this case because the speaker maintains such a steady F0 for so long.