N Cultures
« previous post | next post »
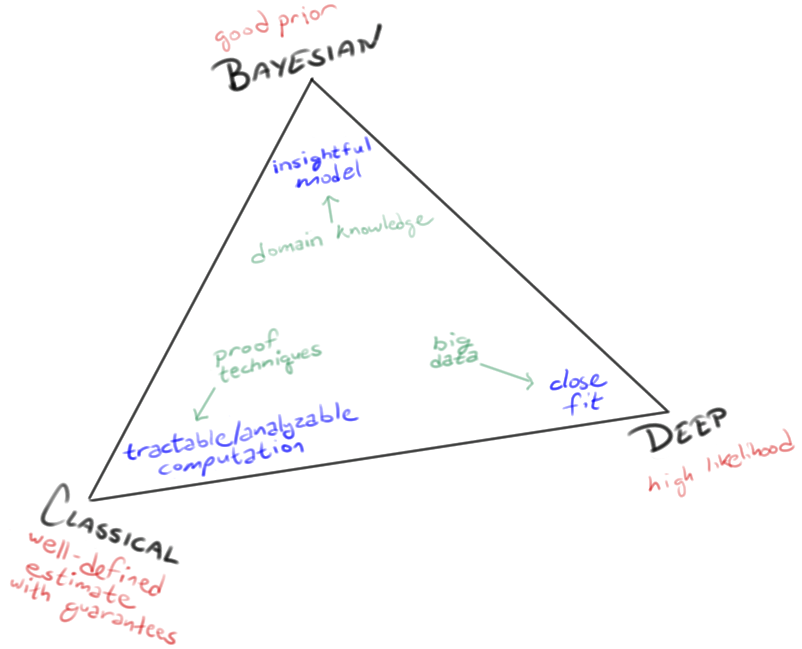
From Jason Eisner, a diagram of "The Three Cultures of Machine Learning":
Jason cites Leo Breiman, "Statistical Modeling: The Two Cultures", Statistical Science 2001, and also mentions the "three competing philosophies" in Bradley Efron, "R. A. Fisher in the 21st century", Statistical Science 1998.
But the idea of distinguishing small integer numbers of cultures in some intellectual domain seems to go back to C.P. Snow's "Two Cultures", with various associated rejoinders and extensions. Snow first used the phrase in a magazine article in 1956, though it's best known through his 1959 lecture and book. More recently, Jerome Kagan picked up the meme in The Three Cultures: Natural Sciences, Social Sciences, and the Humanities in the 21st Century (2009).
There are various theories of organizational culture(s), developed in the last third of the 20th century, some of which yield small-integer taxonomic splits.
And there are earlier taxonomies dividing nation-sized cultures into a small number of well-differentiated classes. A notable example is Ruth Benedict's 1946 work The Crysanthemum and the Sword, which according to Wikipedia "popularized the distinction between guilt cultures and shame cultures". I await a statistical re-interpretation of these ideas in terms of the cultural evolution of loss functions.
Adding the idea of historical progression, we get Adam Smith's notion (1763) that "The four stages of society are hunting, pasturage, farming, and commerce", and its development into more elaborate theories of "conjectural history", such as Karl Marx's mid-19th-century idea of six historical stages.
Jason presents his intellectual simplex in an a-historical frame, but of course there has been a temporal sequence, as the term "classical" suggests.
peter said,
January 29, 2016 @ 6:20 pm
Eisner's comparison of Frequentist and Bayesian approaches, referenced from the second link, here:
https://www.quora.com/For-a-non-expert-what-is-the-difference-between-Bayesian-and-frequentist-approaches/answer/Jason-Eisner?share=1
confuses probability distributions and their unknown parameters. He denotes both by the symbol p. So the usefulness of this exposition for a non-expert is perhaps limited.
Bayesians typically assume that complete ignorance implies that all values of an unknown parameter are equally likely, ie a uniform distribution is appropriate. But one could just as readily assume that complete ignorance implies that all probability distributions of the unknown parameter are equally likely, a very different assumption. It seems odd to privilege just one, specific distribution when in a state of complete ignorance.
peter said,
January 29, 2016 @ 6:29 pm
There are also Birds and Frogs among mathematicians, according to Freeman Dyson:
http://www.ams.org/notices/200902/rtx090200212p.pdf
Andrew Goldstone said,
January 30, 2016 @ 8:02 am
In work on the n=3 case, Kagan is preceded by a great work of intellectual history, Wolf Lepenies's 1985 Die drei Kulturen. Soziologie zwischen Literatur und Wissenschaft (trans. as Between Literature and Science: The Rise of Sociology).
Mike Maxwell said,
February 6, 2016 @ 11:14 pm
But surely the classical division into N cases is "There are 10 kinds of people in the world: those who understand binary arithmetic, and those who don't."