Speech rhythms and brain rhythms
« previous post | next post »
[Warning: More than usually geeky…]
During the past decade or two, there's been a growing body of work arguing for a special connection between endogenous brain rhythms and timing patterns in speech. Thus Anne-Lise Giraud & David Poeppel, "Cortical oscillations and speech processing: emerging computational principles and operations", Nature Neuroscience 2012:
Neuronal oscillations are ubiquitous in the brain and may contribute to cognition in several ways: for example, by segregating information and organizing spike timing. Recent data show that delta, theta and gamma oscillations are specifically engaged by the multi-timescale, quasi-rhythmic properties of speech and can track its dynamics. We argue that they are foundational in speech and language processing, 'packaging' incoming information into units of the appropriate temporal granularity. Such stimulus-brain alignment arguably results from auditory and motor tuning throughout the evolution of speech and language and constitutes a natural model system allowing auditory research to make a unique contribution to the issue of how neural oscillatory activity affects human cognition.
Most of the attention focuses on the "theta band" at about 4-8 Hz, e.g. Huan Luo and David Poeppel, "Phase Patterns of Neuronal Responses Reliably Discriminate Speech in Human Auditory Cortex", Neuron 2007:
How natural speech is represented in the auditory cortex constitutes a major challenge for cognitive neuroscience. Although many single-unit and neuroimaging studies have yielded valuable insights about the processing of speech and matched complex sounds, the mechanisms underlying the analysis of speech dynamics in human auditory cortex remain largely unknown. Here, we show that the phase pattern of theta band (4–8 Hz) responses recorded from human auditory cortex with magnetoencephalography (MEG) reliably tracks and discriminates spoken sentences and that this discrimination ability is correlated with speech intelligibility. The findings suggest that an ∼200 ms temporal window (period of theta oscillation) segments the incoming speech signal, resetting and sliding to track speech dynamics. This hypothesized mechanism for cortical speech analysis is based on the stimulus-induced modulation of inherent cortical rhythms and provides further evidence implicating the syllable as a computational primitive for the representation of spoken language.
Or Uri Hasson et al., "Brain-to-Brain coupling: A mechanism for creating and sharing a social world", Trends in Cognitive Science, 2012:
During speech communication two brains are coupled through an oscillatory signal. Across all languages and contexts, the speech signal has its own amplitude modulation (i.e., it goes up and down in intensity), consisting of a rhythm that ranges between 3–8Hz. This rhythm is roughly the timescale of the speaker’s syllable production (3 to 8 syllables per second). The brain, in particular the neocortex, also produces stereotypical rhythms or oscillations. Recent theories of speech perception point out that the amplitude modulations in speech closely match the structure of the 3–8Hz theta oscillation . This suggests that the speech signal could be coupled and/or resonate (amplify) with ongoing oscillations in the auditory regions of a listener’s brain.
A possible weakness of Luo and Poeppel 2007 (a fascinating and deservedly influential study) was that the same phase analysis that they found to identify the brain responses to different sentences also worked in exactly the same way when applied to the amplitude envelope of the original audio. This suggests that simple modulation of auditory-cortex response by input signal amplitude might be the main mechanism, rather than any more elaborate process of phase-locking of endogenous brain rhythms.
I'm not yet convinced that there's a special role for endogenous rhythms in speech production and perception, beyond the necessary modulation of brain activity by the necessarily cyclic manipulation of speech articulators in production, and by the associated cyclic variation in acoustic amplitudes. All the same, this meme is associated with a range of interesting hypotheses, some of which may well turn out to be true and important.
But I've also noticed that the properties of the overall amplitude-modulation of the speech signal (caused by opening and closing the mouth, by turning voicing and noise-generation mechanisms on and off, and to some extent by varying subglottal pressure) are in some respects not quite as the focus on theta-scale rhythms predicts. To indicate what I'm curious about, I'll show a simple analysis of the TIMIT dataset (which Luo and Poeppel also used) in the 1-15 Hz range.
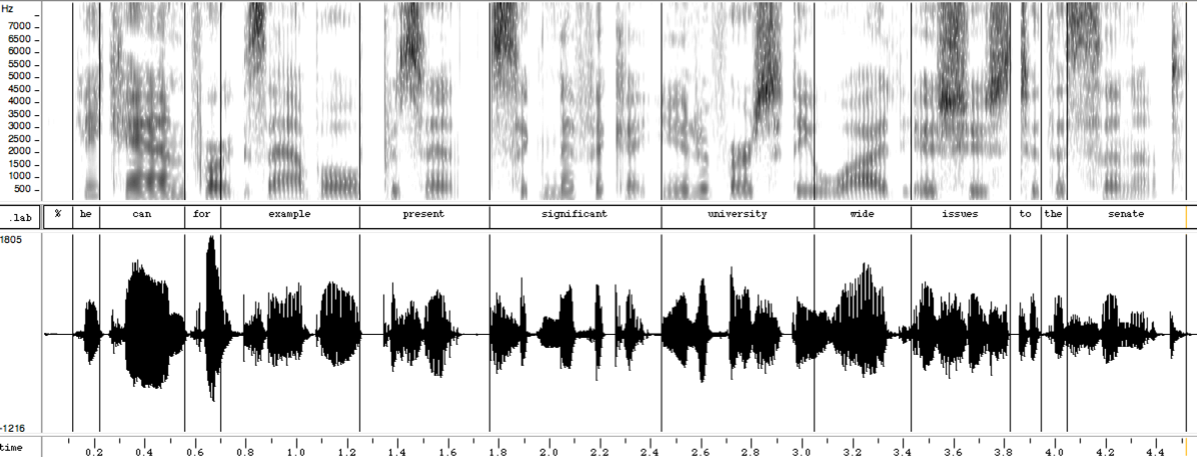
Here's the spectrogram, waveform, and amplitude envelope of a read sentence (one of the 6300 read sentences in TIMIT):
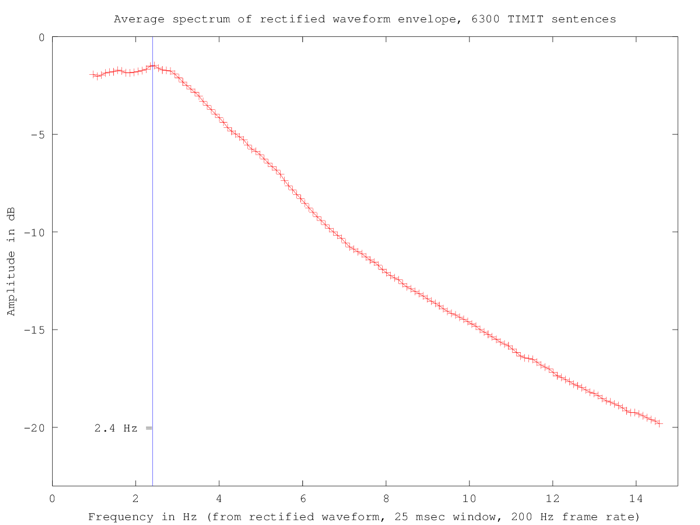
Here's the average spectrum of all 6300 sentences in the range of 1-15 Hz., calculated from the rectified waveforms of all 6300 speech files:
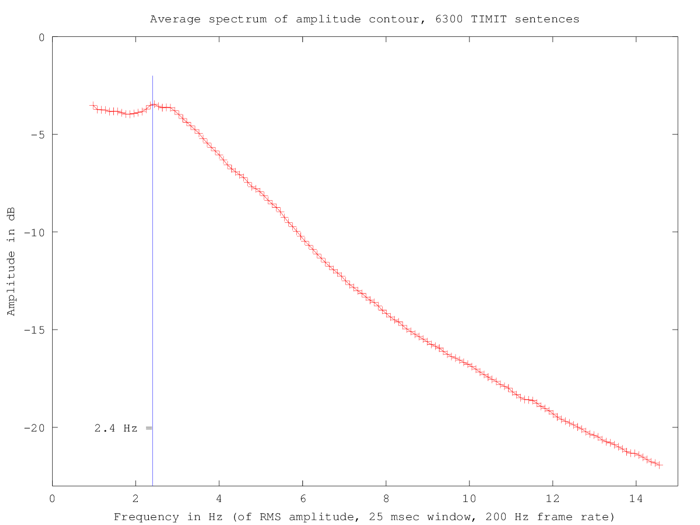
Things don't look very different if we base the spectra on the RMS amplitude in similar 25-msec windows:
2.4 Hz corresponds to a period of 417 msec, which is too long for syllables in this material. In fact, the TIMIT dataset as a whole has 80363 syllables in 16918.1 seconds, for an average of 210.5 msec per syllable, so that 417 msec is within 1% of the average duration of two syllables.
So why is the spectrum roughly flat up to 2.4 Hz or so? And why does there seem to be a different slope between (roughly) 3 and 7.5 Hz, compared to 7.5 to 15 Hz?
One hypothesis might be that this somehow reflects the organization of English speech rhythm into "feet" or "stress groups", typically consisting of a stressed syllable followed by one or more unstressed syllables. But this would predict that similar analysis of material in other languages would show a different pattern — and I'm skeptical, mostly as a matter of principle but also based on the fact that human listeners trying to distinguish between two languages based on lowpass-filtered speech don't typically do very well (e.g. around 65%, where chance is 50%).
Unfortunately there aren't any datasets comparable to TIMIT in other languages; but I'll see what I can come up with as a more-or-less parallel test in languages that are said to be "syllable timed" rather than "stress timed".
If you want to check, challenge, or redo my calculations (and you have a copy of the TIMIT dataset), the needed scripts are doTIMIT1.m, doTIMIT2.m, getENV.m, getRMS.m, and filelist.
MattF said,
December 2, 2013 @ 9:58 am
I guess it's unclear where incoherent averaging is introduced in the two red graphs– e.g., whether it's in the calculation or in the measurement. For example, when you calculate each spectrum (before averaging over sentences) in the first red graph, do you have phase coherence over the whole sentence? If not, won't that introduce a sort of incoherent averaging in each spectrum before you average it with the spectrum of other sentences?
[(myl) After low-pass filtering the rectified waveform, I'm calculating the spectrum for the whole sentence, and then taking the log of the magnitude of the spectrum. So phase differences should be gone at that stage. The sentence-level log amplitude spectra are then averaged.]
D.O. said,
December 2, 2013 @ 10:40 am
I am sorry if I'm missing something obvious, but because you are dealing with positive signal (rms and rectified signals are clearly positive) you should have something like |sin(ωt)| for ordinary sin(ωt) wave, which, of course, has fundamental (angular) frequency 2ω.
[(myl) I'm subtracting the mean value from each sentence's low-passed rectified waveform (or RMS signal), so it's not technically true that the signals are positive, though I don't think this would matter. Anyhow, the observed peak is at half the syllabic frequency, not twice the syllabic frequency.
I suspect that just low-pass filtering of the audio, without rectification, should produce a similar plot of averaged log amplitude spectra. I'll try it later today if I have a few minutes.]
D.O. said,
December 2, 2013 @ 1:46 pm
I am sorry, I did not express myself clearly. Suppose you have a syllable each period T. Then the waveform will be something like |sin(πt/T)| which has (after subtracting the average, of course) frequency 1/(2T).
[(myl) Good point.]
AntC said,
December 2, 2013 @ 3:57 pm
I'm not yet convinced that there's a special role for endogenous rhythms in speech production and perception, …
Indeed. A range of 3 – 8 anything per second sounds like a wide variance. To "resonate", I understand frequencies have to be very close — or close to a whole-number multiplier.
Are the claims that people with faster theta waves speak faster? Or that a speaker's theta waves vary in frequency according to how fast they're talking? Or even that theta waves vary in synch with the metrical pettern within an utterance? Or that a listener's waves 'tune' to the speaker's frequency?
(I'm looking for grounds to rule out that 3 – 8 per second is just coincidence.)
Jerry Friedman said,
December 2, 2013 @ 4:37 pm
D.O.: If you have a syllable each period T, the frequency has to be 1/T. If the waveform is bumpy like the absolute value of a sine wave, if would look like |sin(t/2T)| to get the period to come out right.
(Actually, to my eyeballs the wave in MYL's graph looks more like a sine wave than the absolute value of one, and not very much like either.)
Jerry Friedman said,
December 2, 2013 @ 4:47 pm
But I see the problem. You're assuming that MYL is dealing with the rectified waveform. I think he's dealing with the rectified amplitude: each peak or trough (but nothing in between) is plotted as point equal to the absolute value of the minimum or maximum. If the waveform were 3 sin (2 pi t/T), his blue graph would be a straight line at 3.
(I left the 2 pi out of my previous post.)
D.O. said,
December 2, 2013 @ 4:52 pm
@Jerry Friedman. Yes and no. |sin(πt/T)| has exactly period T, but I was wrong in thinking it should give half-frequency after the Fourier transform.
AntC said,
December 2, 2013 @ 6:11 pm
Hmm, the Hasson et al paper seems to be full of 'evidence' that I'd describe as true, but not relevant.
One of the more relevant references [Lindenburger et al] is to musicians playing together and apparently entraining brain waves in the 3 – 8 Hz range. But are they entraining to each other or to the rhythm in the music? And if the music's beat isn't in the range 3 – 8 Hz, a musician can easily mentally halve or double it to get within that range.
Bill Benzon said,
December 2, 2013 @ 7:22 pm
"But are they entraining to each other or to the rhythm in the music?"
What's the difference? After all, the musicians themselves are creating the music. It has no existence apart from them. It's not as though they can entrain to one another but not to the music, or vice versa.
See The Sound of Many Hands Clapping, which, however, says nothing about brainwaves, but something about entrainment to a common rhythm. Actually, it's more interesting than that.
AntC said,
December 3, 2013 @ 12:24 am
Thanks Bill, what's the difference? is the point!
We don't need to posit that there's synching of brainwaves going on (by Occam's razor).
(And thanks for the ref to the hand-clapping. A pity that in that experiment they didn't have the audience hitched up to EEG's ;-)
Bill Benzon said,
December 3, 2013 @ 5:21 am
OK, gotcha AntC. That is to say, whatever is going on, it's not some mystical group-wide Vulcan mind-meld where people are directly "goking" (another SF franchise) one another's brain waves and THEN producing physical signals that are miraculously in synch with those brain waves. There's no miracle here.
We've got a physical system passing signals. Some signal paths exist inside brains and are electro-chemical. Other signal paths are external and use mechanical waves in the air. The system as a whole displays rhythmic activity.
On the clapping, if you google a bit you might come up with a longer and unpublished version of the clapping study – I did, but that was some years ago and, though I've still got the paper, I've lost the link. The authors reported that sometimes at Communist Party events (remember where this research was done) you would get the regime of rhythmic clapping but NOT the louder desynchronized regime. The authors suggested that on those occasions there was no enthusiasm for the speaker, hence no loud desynchronized clapping, but the audience would still express solidarity through synchronization.
So, in the case – which they reported in the Nature paper – where clapping drifts back and forth between those two regimes, we're multiplexing two signals through that common external channel. One expressing enthusiasm for the performance and the other expresses solidarity within the audience group. I'd love to know the brain circuits involved in that.
In fact I've got some notes in which I make a WAGish guess about what's going on. The guess is that the synchrony comes from a cortical region (supplemental motor cortex I belive) while the enthusiasm is subcortical. That is, the two signals come from distinctly different brain regions. And – another WAG – there is no brain region that's directly riding herd on those two regions. Rather, they coordinate through the clapping activity itself.
Now, if you try to clap faster and faster you'll find that you quickly reach a point where you can't go any faster and you can't maintain either. You've got to relax. When we've got a whole group subject to that limit, you get drifting back and forth between two regimes. The enthusiasm regime comes up against the motor limits of the system, forcing the system to relax, at which point the solidarity regime can dominate the signal. Enthusiasm builds up and….
WAG = wild ass guess
Terry Hunt said,
December 3, 2013 @ 8:49 am
@ Bill Benzon
As a geeky, skiffy quibble: it's "grokking" (from Robert A. Heinlein's Stranger in a Strange Land).
Bill Benzon said,
December 3, 2013 @ 9:34 am
Thanks, Terry Hunt, spelling never was my strong suit.
Ron Netsell said,
August 2, 2014 @ 4:23 pm
By now I assume you've read "Oscillators and syllables: a cautionary note."
He concurs with you, for the most part, and I agree with his "caution."
cummins_oscillators_2012.pdf (404 KB)
[(myl) A full reference: Cummins, Fred. "Oscillators and syllables: a cautionary note." Frontiers in psychology 3 (2012): 364.]