Two cultures
« previous post | next post »
SMBC from a few weeks ago:
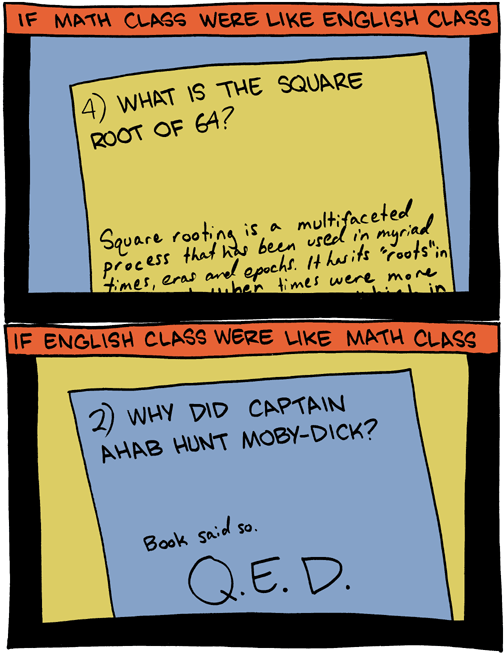
In my limited experience, it's fairly common to get some intellectual history in math courses — when and why and by whom a problem was posed, who tried to solve it how, what unexpected connections and applications it turned out to have when, and so on. However, I don't think that I ever encountered an exam question that asked about stuff of this sort. Has there ever been a calculus exam that asked something like "What was the physical problem that led Joseph Fourier to invent the series named for him? Describe the experimental apparatus that he used to test his idea."
This cultural expectation runs deep. Some years ago, when I was teaching Introduction to Cognitive Science, an engineering student came to me after the midterm exam to complain. There had been a question asking the students to connect a list of people (e.g. Turing, Frege, etc.) with a list of ideas (universal computation, predicate calculus, etc.). I thought that the question was pretty much a gift, but the student had gotten it wrong, and she was clearly not used to getting things wrong.
"This is ridiculous", she said. "If I know how to solve a problem, what does it matter whether I know who first figured it out?" She had assumed that the intellectual-history aspect of the lectures was a sort of non-nutritive filler, introduced for the benefit of those inferior students who couldn't digest a more concentrated and abstract diet.
After that, I tried to be more careful to explain in an early lecture how the course was going to work.
tudza said,
May 27, 2010 @ 6:04 am
Uh, is this going to be on the test?
Nick Lamb said,
May 27, 2010 @ 6:35 am
So, in theory the purpose of the test is to find out whether the student understood the material. So what I'm left unclear on is, how did your test question do that? It seems as though they get the best marks (for that question) for rote learning.
[(myl) In my opinion, an educated citizen of the modern world should know who Alan Turing was and what he did, and similarly for a list of other people that includes Gottlob Frege. I suppose that a certain amount of "rote learning" is involved in acquiring knowledge of this kind. I viewed the exam question under discussion as a "gift" because it was so easy and superficial — it's not like I asked them to sketch Turing's argument in "On Computable Numbers", or compare and contrast his approach with Church's, or explain why Frege's approach was a step forward over syllogistic logic, though those issues were covered in class.]
Henning Makholm said,
May 27, 2010 @ 6:44 am
When I studied math, there was a required "history of mathematics" course, taught by a mathematician from the mathematics department, that contained exactly that sort of thing.
It matters because being academically qualified about a matter is not just a question of being able to "solve problems", but also about being able to discuss the matter intelligently with other experts. Using the inventor's name as a shorthand reference to a complex group of ideas is so universally done that you won't be able to communicate effectively without knowing the relevant famous names.
And knowing about which ideas historically led to which other ideas is indispensable for quickly recognizing forward and backward steps in your own idea development. (Couldn't we just do so-and-so? … Sure, Leibniz tried that, and it sort-of worked most of the time, but making it reliable turned out to be hard and eventually resulted in just the trouble you're trying to avoid here).
Ray Girvan said,
May 27, 2010 @ 6:46 am
assumed that the intellectual-history aspect of the lectures was a sort of non-nutritive filler, introduced for the benefit of those inferior students who couldn't digest a more concentrated and abstract diet.
I'm getting déjà vu there. When I was at university, one of the first-year Natural Sciences options was History and Philosophy of Science (which I rather wish I'd taken). It had at the time a low reputation among hard-science students, being viewed as part of the "Rugby Tripos" (alleged easy-option subjects for students allegedly admitted for their sporting rather than academic ability).
Jonathan Badger said,
May 27, 2010 @ 6:54 am
A bit over twenty years ago when I took calculus I remember that there a bonus question on one of the tests that asked something to the affect "What is an interesting fact about L'Hôpital's rule?", with the desired answer that Guillaume de L'Hôpital apparently didn't discover it himself but had hired Johann Bernoulli to come up with discoveries for him, which included the rule now known as L'Hôpital's rule.
Ian Preston said,
May 27, 2010 @ 7:24 am
I've sat, set and marked plenty of exams with maths content. You don't get good marks for saying: "Book said so. Q.E.D."
Neal Goldfarb said,
May 27, 2010 @ 8:02 am
<blockquote?You don't get good marks for saying: "Book said so. Q.E.D."
Quite right. The correct answer is "The book said so."
Ray Girvan said,
May 27, 2010 @ 8:42 am
The trouble I recall with English as a subject was that the answers could often be expressed extremely tersely …
… but examiners expect you to waffle for three pages, with quotations, to say it.
Q.E.D.
Max said,
May 27, 2010 @ 8:51 am
@Ian Preston
I think you may have missed the joke. From a mathematical perspective, the correct answer to a question asking for for a reason for some fact is a proof. "Book said so" is not a proof of the fact that the terms of every convergent series converge to zero, but it *is* a proof that Ahab hunted Moby Dick. When we are studying a work of literature, the facts stated in that work are our axioms.
Mark P said,
May 27, 2010 @ 8:54 am
"If I know how to solve a problem …"
That sounds like the engineer's approach. I've worked with smart engineers who can find solutions (to well-defined, previously-solved problems) but who don't understand the basic physics behind the problem or the solution. And that's in their own field. Granted, it's usually engineers with bachelor's degrees.
But still …
D.O. said,
May 27, 2010 @ 9:06 am
First rule of teaching: students will complain no matter what you do.
As for the first exam question (or should I say question 4?), the correct answer is "It is not possible to find a square root, they are all rounded."
J. Goard said,
May 27, 2010 @ 9:16 am
Huh?
Not only does "book said so" not properly answer the question, but it's a nonsensical response to the "why" question that was asked. To what does "so" corefer? The question asks for a reason, so the only way the answer works is if it means "Because he [=Ahab] read the book (that you and I know about) which instructed him to hunt Moby Dick."
Fred said,
May 27, 2010 @ 9:17 am
This is a problem of expectations.
Normally when this sort of content is mentioned, it *is* "filler", so much so that most instructors would not even bother mentioning it won't be tested. So it's expected that only information directly related to the course, is directly related to the course.
Was anything of that nature included in past exams, on mid-terms, etc?
Ian Preston said,
May 27, 2010 @ 9:19 am
@Max: The question didn't ask whether or how you know he hunted Moby Dick, it asked why. Maybe I still miss the joke – it only makes sense to me as a joke about brevity.
Ginger Yellow said,
May 27, 2010 @ 9:20 am
"The trouble I recall with English as a subject was that the answers could often be expressed extremely tersely …
… but examiners expect you to waffle for three pages, with quotations, to say it."
That's because English Lit as an academic subject isn't about getting the "right" answer, whatever that means, but about engaging with the material, making an argument and supporting it with evidence. Your hypothetical answer isn't exactly interesting, is it?
Coffee on the Quad » Academic Cultures? Math and English said,
May 27, 2010 @ 9:44 am
[…] Cultures? Math and English Posted May 27, 2010 By Collin The Language Log has a discussion of a Saturday Morning Breakfast […]
Ian Preston said,
May 27, 2010 @ 9:47 am
Let L(i,t) be the number of legs of individual i at time t. Let T be the time at which Ahab meets Moby Dick. Let M(L,t) denote the population mean at time t, E_i L(i,t). Then for all t0 < T < t1 L(A,t0) > M(L,t0) and L(A,t1) = L(A,t0)-1 < M(L,t1) where A denotes Ahab.
marie-lucie said,
May 27, 2010 @ 9:52 am
"engaging with the material"
I seem to read this everywhere lately. It might be the recency illusion, but my point is what does it actually mean? I keep thinking of "wrestling" with the material. What else can one "engage with", as opposed to "engage in"?
nonpoptheorist said,
May 27, 2010 @ 9:59 am
When students decide to move into secondary and additional reading they learn some interesting facts that help to explain the sociology of their subject. The changing community of the time, accepted laws and ideas, the branching off of ideas that worked or didn't that we should maybe be still debating today. I'm not sure if it is shock or amusement learning about the greats arguing their second PhD thesis for days against their own tutors, or the secondhand research data used on totems that turned out to be bad data. Little quips about certain people liking contemporary students' ideas and methods even though they go against their own and acceptance today (the 'little dagger' and politeness) Learning theories by rote is enough to scrape by, but the world becomes so much more colourful knowing more about the lives and paths of those we read about.
DonBoy said,
May 27, 2010 @ 10:12 am
If the student is in the middle of a course called "Introduction to Cognitive Science" and believes that it involves "know[ing] how to solve a problem", something's already gone wrong. ("Consciousness…done and done.")
Jim said,
May 27, 2010 @ 10:32 am
Don't forget the votey: http://www.smbc-comics.com/comics/20100505after.gif
9th floor said,
May 27, 2010 @ 10:33 am
Your engineeering student would have been even more dismayed had she, to fulfill some humanties requirement, accidentally enrolled in an art history class I once took. The instructor would regularly punctuate his lecture with "amusing anecdotes" from the lives of the artists under discussion, apparently to provide some background texture and to break the monotony of the otherwise endless stream of names and dates, influences and analyses. These anecdotes were themselves accompanied by the sound of the dropping of pens, stretching, and muttered conversation between the students, who were grateful for the chance to stop writing and relax for 5 minutes before the lecture resumed.
At the midterm, we discovered that half the exam consisted of multiple choice questions on precise details from those anecdotes.
Simon Cauchi said,
May 27, 2010 @ 10:48 am
Why has no one commented on the witty allusion to C. P. Snow in Mark Liberman's title? Leavis's response, if I remember rightly, was: "Luddites? Or Is There One Culture?"
Russinoff said,
May 27, 2010 @ 11:02 am
When I taught calculus to freshmen, I occasionally included a question like this on a test, for the purpose of later discussing the significance of the high percentage of missing or wrong answers ("Albert Einstein", "my high school geometry teacher, Miss Armstrong", etc.):
Name a well know dead mathematician.
N said,
May 27, 2010 @ 11:04 am
All the above comments are sidestepping an issue I think is at the heart of this:
Linguistics students generally do not have instruction on rigorous scientific practice.
Jeff DeMarco said,
May 27, 2010 @ 11:10 am
Part of the humor in that cartoon is that *neither* response answers the questions asked!
Jens Fiederer said,
May 27, 2010 @ 11:20 am
> a question asking the students to connect a list of people (e.g. Turing,
> Frege, etc.) with a list of ideas (universal computation, predicate
> calculus, etc.).
This is a valid question for a course on "History of Mathematics".
It is not a valid question for a course on "Mathematics".
As Cognitive Science goes, I'm not sure HOW its culture would stand on that question.
Mark P said,
May 27, 2010 @ 11:21 am
@Jeff Demarco, yes, i think the point of the cartoon is not that the classes would be taught that way, but that students would answer questions that way.
Ray Girvan said,
May 27, 2010 @ 12:03 pm
Ginger Yellow: engaging with the material
Sorry, I was just stirring. My point really was that at school level (to which the cartoon presumably refers, judging by the elementary math question) I don't think there is much difference in approaches, except in level of detail. As study guides such as Sparknotes and book equivalents attest, there are analyses of character and motivation that examiners will view as "right". At that level, it would take a rare student to risk breaking out of that framework and arguing something unconventional: say, that Ahab has Body Integrity Identity Disorder and stuck his leg into the jaws of a "parmacetty" in order to have a legitimate reason for it to be amputated.
J. C. Lorraine said,
May 27, 2010 @ 12:10 pm
As Cognitive Science goes, I'm not sure HOW its culture would stand on that question.
Well, as a sometime teacher of cognitive psychology and cognitive science,* I have to say that it simply wouldn't occur to me to include such material. It's not that I consider it unimportant–rather the contrary–but that I don't think it's relevant enough to warrant the elimination of other material. I feel much the same way about Darwin, Hume, and (for that matter) Bach; they're all obviously important, and an educated person should know about them, but there is not time to cover everything in detail.
Now, having said that, I *did* cover Descartes because I considered his work to be vital to students' comprehension of the limitations of scientific inquiry, particularly in the cognitive sciences. As far as I know, other instructors don't cover Descartes, so maybe all of this merely reflects our own intellectual whims. I'd be interested to hear how Frege and Turing (I keep almost writing Tulving) are incorporated into a cognitive science curriculum.
*Assuming that these two are distinct….
Sean Edison-Albright said,
May 27, 2010 @ 12:32 pm
Marie-Lucie:
One can also "engage with" people and nations.
mollymooly said,
May 27, 2010 @ 12:46 pm
@marie-lucie
I think "engage with" means "enter into a constructive dialog based on mututal respect with, rather than taking the easier option(s) of disdain or defiance". I don't know the French word, but an older English word is "détente".
Ginger Yellow said,
May 27, 2010 @ 12:47 pm
"I seem to read this everywhere lately. It might be the recency illusion, but my point is what does it actually mean? I keep thinking of "wrestling" with the material."
Funny you should say that, as I actually decided not to use "wrestling" and opted for "engaging". I can't speak for anyone else, but for me it means reading the material, understanding it (or attempting to in some cases), and placing it in context (literary, historical etc), among other things.
Cialan said,
May 27, 2010 @ 1:17 pm
@Jens Fiederer:
>This is a valid question for a course on "History of Mathematics".
>It is not a valid question for a course on "Mathematics".
Who determines what is or isn't a valid question? If the instructor makes it clear (at the beginning of the course or while covering the particular topic) that less-conventionally-tested topics deemed relevant to the material will be included in the course and on examinations, and his/her department is fine with this idea, is it still not a valid question?
This tangent of the discussion appeals to me because it is something with which I have been grappling as a learner and instructor of second languages. Is it a "gimme," as in MYL's course, to have a substantial matching section on the cultural topics (country, region, or social fabric) given in that chapter or presented in class in the previous weeks? Does that section take away from the power of that test to evaluate a student's language ability? Or is it essential that a student with basic knowledge of a language also have basic factual knowledge about every country or region studied?
This approach seems to fit more with Ginger Yellow's "engaging with the material," but I can also see how some would equate it to "rote learning," as Nick Lamb commented.
marie-lucie said,
May 27, 2010 @ 1:17 pm
mollymooly, Ginger Yellow,
thank you for your contributions. I had forgotten about the "engage with peoples and nations" context, which I was just reading about in an article on Obama's latest speech. It is in the context of studying literature or other intellectual pursuits that I am not sure – those things are abstract and do not answer back, unless in the figurative sense of "repaying study". Does it just mean "studying the material in depth"?
I am kind of surprised to learn that "détente" is an English word which requires a French equivalent! In French it means basically "release of tension", which may be concrete (in the act of shooting a gun, in a tensed then relaxed muscle, in a person relaxing in a bath. etc) or figurative (a person participating in leisure activities, or in the relaxing of tense relations between people or countries). French "détente" would be the result of "engaging with perceived enemies", not the act of engagement itself.
Ginger Yellow said,
May 27, 2010 @ 1:38 pm
"Does it just mean "studying the material in depth"?"
Something like that, but it speaks to the parameters of the depth, if you see what I mean. It's not just a question of learning the text by heart, but of figuring out why it is the way it is, and what's important (or not) about that.
marie-lucie said,
May 27, 2010 @ 1:42 pm
GY, That's what I mean by "studying the material in depth". Memorizing the text may be a preliminary to that type of study, but is not equivalent to it. But I thought perhaps "engage with the material" had yet another dimension which I could not grasp.
Coby Lubliner said,
May 27, 2010 @ 1:59 pm
Marie-Lucie: could it be that "engage with" in this context bothers you because it's so different from s'engager avec (which means "get involved with" or "join")?
blahedo said,
May 27, 2010 @ 2:15 pm
It's tangential, but I found @Ian Preston's comment to be quite remarkable for reasons unrelated to its semantic content:
I've sat, set and marked plenty of exams with maths content. You don't get good marks for saying: "Book said so. Q.E.D."
These sentences are perfectly understandable to (most?) Americans, but the density of Britishism here is staggering (and none of it to do with spelling). I've even used most of these terms independently of each other, but the gestalt effect still surprised me. My own rendering would have been:
I've taken, written, and graded plenty of exams/tests with math content. You don't get good scores/grades for saying: "Book said so. Q.E.D."
I wouldn't have expected such divergence, especially in academia where there's been more contact across the ocean than elsewhere, I think.
Sili said,
May 27, 2010 @ 2:16 pm
History of Mathematics is in fact a required didactic component of the Danish M.Sc. (in maths), if one wants to teach High School.
I didn't, so now I need to get the exam to qualify for my job … (I actually took HoM and enjoyed it, just felt too busy to take the exam. I hate oral exams, and this one was sans preparation.)
wren ng thornton said,
May 27, 2010 @ 2:53 pm
@J. C. Lorraine:
Alan Turing's work is immensely important to modern cognitive science. Without understanding the significance of Turing's work, there's no way that a student could appreciate the reasons behind the Turing-functionalist philosophy which has dominated contemporary conceptions of how the brain works and the role it plays in cognition. The idea of the brain as a computer and the idea that we can understand and construct a model of the brain's operation is a radical departure from the behavioralism that had previously dominated American psychology. Noam Chomsky's critique of B.F. Skinner laid the groundwork for the transition, but Chomsky never would have been in that position were not for Turing's work and the beginnings of computer science as a field independent from mathematics.
Similarly, I'd say that Hume's Enquiry Concerning Human Understanding is as important as Descartes' Meditations for grappling with the prehistory of cognitive science. Without both of them one doesn't get a good view on the complete space of thinking at the time.
Gottlob Frege seems less relevant. Though if your cognitive science has a large dose of philosophy of language in it, then clearly Frege must be discussed at some point in order to lay the foundations for the rest of the discussion.
Ginger Yellow said,
May 27, 2010 @ 3:06 pm
"These sentences are perfectly understandable to (most?) Americans, but the density of Britishism here is staggering (and none of it to do with spelling). "
You should submit it next time Lynneguist does her "Most mutually incomprehensible British/American sentence" competition.
Army1987 said,
May 27, 2010 @ 3:14 pm
In an oral exam I was (jokingly) asked whether I knew Noether was a woman.
marie-lucie said,
May 27, 2010 @ 3:15 pm
Coby: Marie-Lucie: could it be that "engage with" in this context bothers you because it's so different from s'engager avec (which means "get involved with" or "join")?
There are numerous instances of "faux amis" between French and Englishm, and I know quite a number of them. Since I have lived mostly in English for several decades, my French is now quaintly old-fashioned, because it does not contain new anglicismes such as "s'engager avec". I think I can keep my two languages separate and do not enjoy seeing them mixed up in almost every current French text I read.
In my now old-fashioned, or backward, idiolect, I would use "s'engager" to mean "to join (up)" (s'engager [dans l'armée], dans la marine, etc) or as a formal way of saying "go into" (s'engager dans une voie sans issue 'to enter a deadend street' [literally or figuratively], s'engager dans la politique, etc)), with the preposition "dans" not "avec" , as well as with the preposition "à" to indicate a contractual promise (je m'engage à respecter les règles en vigueur). I quite understand that these meanings are quite different from that of "engage with (something)" (even though I am not sntirely sure of the nuances of its meaning) and had not even thought of comparing the English expression with "s'engager".
I think I have run into "s'engager avec" in writing, to mean apparently "to get involved with" in the sense of a romantic relationship, or maybe even joining a team (for work or play), but these are not expressions that I would use myself. Obviously, "engage with a text" has neither the old nor the new meanings of "s'engager".
Alex Fink said,
May 27, 2010 @ 3:19 pm
Paul Graham has an interesting take on the situation.
Writing persuasively (or its degenerate cousin, waffling on for pages with quotations) is the proper topic of a course in composition or rhetoric; English literature has nothing necessary to do with it. Surely at least some of the students who find English class a tedious waste of time would find it a little better if they wrote more essays on subject matter they cared about.
In the US before 1892, literature and composition were separate high school subjects. Graham has it that they were unified in imitation of the development in universities: some decades before, the new fashion that professors be researchers, not just lecturers, had meant that many professors who taught English composition took up research in English literature, as the nearest suitable topic of study.
J. C. Lorraine said,
May 27, 2010 @ 3:22 pm
The idea of the brain as a computer and the idea that we can understand and construct a model of the brain's operation is a radical departure from the behavioralism that had previously dominated American psychology.
True, but it isn't so radical a departure from the neuropsychological and neurological tradition that preceded (and, for that matter, was continuous with) behaviorism. Then again, I also think that "the idea of the brain as a computer" is quite perilous and leads to all sorts of misunderstandings, much like "the idea of the brain as a hydraulic mechanism." (I do discuss Lashley, as you can probably tell.)
J. C. Lorraine said,
May 27, 2010 @ 3:26 pm
In the US before 1892, literature and composition were separate high school subjects.
In fact, they were separate in my high school (and my elementary school), and with good reason. Composition skills are obviously important to the study of literature, but when a literature class devotes time to improving students' composition skills, it necessarily detracts from, well, the study of *literature*.
Blake Stacey said,
May 27, 2010 @ 3:35 pm
Entirely true.
Of course, the names we use as shorthand references don't necessarily match up to history all that well — history is messy, but shorthand must be by nature concise. (The joke is that a mathematical theorem must be named after the third person to discover it, because Gauss and Euler discovered everything first.) We run the risk of teaching "scientist's history of science"; as Richard Feynman once said, "What I am telling you is a sort of conventionalized myth-story that the physicists tell to their students, and those students tell to their students, and is not necessarily related to the actual historical development, which I do not really know!" This is how textbook cardboard gets made.
Young Philo Teacher said,
May 27, 2010 @ 4:11 pm
@JC Lorraine, I was struck by that last bold comment b/c I agree with it, though I would never have the guts to say/write it publicly.
I'm a late-stage philosophy ABD student, and
indentured servantpart-time adjunct teacher, and I can confidently say that one in my position must always, when describing her pedagogy, make a big deal about persuasive composition skills as a major component of her course objectives. It is difficult to do this in good faith. In a typical introductory philosophy course, with +/- 35 students, I've not found a good way to work with students on their composition skills while also focusing on the argumentative structure, insights, sheer thrill, etc., of the Republic, Meditations, Enquiry, etc. Yet, from my experience, the culture of academic philosophy requires that we rank composition right alongside comprehension and appreciation of primary texts as equivalent course objectives.Anyway, I agree with your comment in the sense that if I grade student papers with the aim of improving their prose composition skills, then it really does limit my ability to focus simultaneously on analytical, argumentative, comprehension skills.
Ray Girvan said,
May 27, 2010 @ 4:20 pm
Alex Fink: Paul Graham has an interesting take on the situation.
Verrry nice, and spot on. At school I loathed English Literature because we were asked exactly to produce that kind of take-a-position-and-justify-it essay; or else answer dull character-motivation questions (e.g. "Compare and contrast Paul's relationships with Miriam and with Clara").
I didn't get into writing about literature until decades later, on reading litcrit works like John Sutherland's Was Heathcliff a Murderer? et al, which brought home the realisation that it's allowed to write essays about literature from a viewpoint of "That's odd/interesting. What can I find out about it? How does it connect?"
peter said,
May 27, 2010 @ 5:34 pm
Ray Girvan: I had an enthralling high-school English teacher who used to say there was only one valid question in literary criticism, namely the question you ask after leaving a movie: "Well, what did you think?"
Andrew (not the same one) said,
May 27, 2010 @ 5:35 pm
blahedo: Interestingly, in some forms of traditional British English 'writing' an exam actually meant 'sitting' or 'taking' it (i.e. writing the answers, not the questions), so there would have been serious potential for confsuion here.
Jair said,
May 27, 2010 @ 5:51 pm
I think that knowing a little of the history of mathematics is vital to understanding it, and I hate that it's often obscured. Many students are misled by the slick presentations of their textbooks that hide the many changes in perspective that go hand-in-hand with the formation of a theory. If you read the text for a high school algebra book, you might get the impression that somebody just made up the idea of a number called i that, when you square it, you get -1, and discovered facts like i^5 = i, and then many years later it was found useful for engineering or something. You would think that mathematics is built by screwing around with some symbols and trying different things out until maybe at some point some physicist likes it. In fact most developments in mathematics have gone hand-in-hand with their application. Mathematics is built by asking a really good question and working your way towards a potential answer, not by pushing random symbols around and making up numbers that don't exist. You must know the history of the ideas to understand where concepts in mathematics come from.
Keith M Ellis said,
May 27, 2010 @ 6:03 pm
I attended a very unusual liberal arts college with an entirely mandatory curriculum (only one degree available) that included a full four years of mathematics and three of what it calls "laboratory science". What's unusual is that both are taught from primary sources and chronologically through the subjects' development. (Science topics are more complicated; but generally lab follows the development of western science chronologically yet necessarily follows certain sciences in particular outside of the general chronology. And physics is heavily dependent upon the progress of the math section.)
While the math/science sections appear to be "history of" courses, this is not really the case because the student learns and works through all the mathematics and much of the science, performing a great many historical experiments.
The rest of the curriculum, and which normally receives more outsider attention, is philosophy, literature, and history.
I had previously attended a conventional university as a physics major and I have a strong math/science orientation.
I found this approach to math and science to be extremely illuminating in ways that can be very important to actually doing math and science. Certainly, the education is deficient in a purely technical sense—students fail to learn and become adept at currently standard technique. If one moves on to grad school in math or science, this is a lack that must be addressed.
However, at the cost of technical mastery is gained a strong conceptual mastery. Not only in the sense that learning each important development in its foundational context provides a much stronger sense of its intellectual scope and utility; but also because one acquires a profound sense of the interrelationships between ideas in the intellectual tapestry of math as whole, science as a whole, and individual scientific disciplines. (Not to mention that one profitably becomes very suspicious of the "now we know everything" hubris that every era of science has exhibited.)
What I've pondered for twenty years is just how much value this provides to your average working scientist, relative to its costs (primarily in technical mastery which is a deficit that one is required to furiously address in grad school). And for the average working scientist, I'd say "not much". Or worse. The average working scientist these days is a hyper-specialized technician. That's not a bad thing. Modern science is an extraordinarily complex, highly technical, collaborative endeavor. What it needs are hyper-specialized technicians.
On the other hand, there will always be a small cadre of highly creative scientists who explore new frontiers and ask questions no one has previously thought to ask. Those folk will be well served, in my opinion, by a very context-rich math and science education.
In any case, I (ironically, given my education) am skeptical of the one-size-fits-all approach and am suspicious of assertions of the form "a good science education (must be/must not be) X". Someone mentioned engineers earlier. They're sort of notorious for this "don't waste time on this fluff" mentality. But that's part of what makes them good engineers.
q said,
May 27, 2010 @ 6:07 pm
I took an Introduction to Computation Theory course in college which had as required reading a history of computation theory. And we even had an essay question on the test relating to that history! Probably my favorite class during my undergrad days.
peter said,
May 27, 2010 @ 6:38 pm
@wren ng thornton: Perhaps Gottlob Frege is included in a course on Cognitive Science as an example of someone unable to accept new concepts, even after they are explained to him. He famously misunderstood the axiomatic approach to geometry of Mario Pieri and David Hilbert, arguing in letters to Hilbert that either Euclidean geometry was true or else non-Euclidean geometry was true, and so mathematicians should study one or the other, but not both. Hilbert eventually stopped writing to him.
peter said,
May 27, 2010 @ 6:56 pm
Jair (May 27, 2010 @ 5:51 pm):
While it is true to say that much of pure mathematics has arisen in response to real-world problems, and was developed in tandem with their modeling and solution, this is not true of all pure mathematics. There are many examples of mathematicians playing idly with ideas and seeing where they lead, and only afterwards (sometimes centuries afterwards) the ideas finding application. Examples include: non-Euclidean geometry (applied later to relativity theory), Boolean algebra (electronic circuits), the mathematics of the infinite (statistical physics, probability theory, computer science), the mathematics of origami (design of space-craft, industrial packing). And certainly the stories which pure mathematicians tell their students emphasize these idle-hands-make-great-math episodes rather than the development-in-tandem-with-apps episodes. (Applied mathematicians may tell their students different stories, of course.)
Kapitano said,
May 27, 2010 @ 6:58 pm
A student who knows how to do a task when told to do it gets a bare pass.
A student who can identify which tools they need to complete the task gets a good pass.
A student who can explain why this tool is appropriate for that task…understands the tool and the task because they know the history of both.
Clarissa at Talk to the Clouds said,
May 27, 2010 @ 9:01 pm
Interesting timing–my husband is grading math final exams right now, and the answers involve lots of written explanations interpreting the answers they got. Students can't just crunch numbers through formulate in his class (what good is math without understanding the interpretation of the results?). In homework assignments, a lot of their grade depends not only on their calculations but on how well they are able to explain why, for example, he should choose one cell phone plan over another, or why an insurance set-up at a company is fair or unfair (they had to write that one from both the management's and the workers' viewpoints, as I recall). So no, they can't just refer to the book–they won't be able to pass.
Bad math academic culture is a plague, but so is bad English academic culture. I blame the ridiculous notion that college teachers don't need petty hindrances such as substantial pedagogical training. (I teach English. Don't get me started.)
Buck Ritter said,
May 27, 2010 @ 9:06 pm
Or, to translate into the real world, an A-, an A, and an A+.
Rubrick said,
May 27, 2010 @ 10:50 pm
I like this a lot, but I think the second panel is just slightly off the mark. I think "Because Melville made him" would be more apt (though probably less funny). The book is a consequence.
I've always been terribly impatient with the style of literary analysis that treats fictional characters as though they were real people, with real motivations. Unless it's merely a test of reading comprehension, the only sensible answer to "Why did Huck Finn decide to help Jim?" is "Twain thought it would be a good idea". Now, why Twain did that might be a very interesting question indeed. Huck, though? He pretty much did what he was told. That's just a fictional character's lot in life.
J. C. Lorraine said,
May 27, 2010 @ 11:43 pm
In a typical introductory philosophy course, with +/- 35 students, I've not found a good way to work with students on their composition skills while also focusing on the argumentative structure, insights, sheer thrill, etc., of the Republic, Meditations, Enquiry, etc.
I wish I had a good solution. On some level, both my students and I seem to feel that psychology and composition are different domains–they're willing to listen to me about the former but not so much about the latter, and I always feel as though I'm overstepping the bounds a bit when I critique their composition skills. At the same time, sometimes the problems are so severe that I can't figure out what they're saying, and I just can't let that pass.
I've encountered a few approaches that seem to be at least partially effective. A few years ago, I adjuncted at a school with a very well-run remedial writing program. At the beginning of the year, students were triaged into three groups: the excellent writers (who were waved ahead into the regular curriculum), the mediocre (who went through one course on college-level writing), and the people who pretty clearly had some sort of verbal learning difficulty. Obviously it wasn't magic–the groups were never made equal–but the last group in particular tended to show some degree of progress and at least learned some strategies to compensate for their major problems. To me, that's a good approach, because it connects these students with people who at least have some idea how to help them. Beyond a certain point, asking me to teach students composition skills is like asking me to help a stutterer; it's important, and it's a good thing to do, but I don't really know how to do it and might only make things worse if I try.
That aside, I tend to restrict my main critiques to issues of comprehension, and I try to explain *why* I didn't understand. For instance, when I come across an ambiguous sentence, I give them the two possible alternatives and ask them which they meant. I *think* this helps, but I don't have the slightest bit of data to support that–which is another problem….
wren ng thornton said,
May 28, 2010 @ 12:49 am
@J. C. Lorraine:
Oh, without a doubt :) Nevertheless, it is the common way people think of the brain these days: as just a CPU, with our thoughts acting like software running on it. There's some movement away from that ideology and towards the situated, embodied, dynamical perspective but TM-functionalism is still the default position. Even people like Searle, who are vociferously opposed to the classical artificial intelligence paradigm, still typically frame their discourse in a way that assumes the basic framework of TM-functionalism (and the implicit dualism contained therein).
Perhaps; my knowledge of the history of neuroscience is a bit thin.
In any case, for the variety of cognitive science coming from psychology, philosophy, linguistics, and artificial intelligence, every student of the subject should be aware of Alan Turing, the theoretical importance of Turing machines, and the impact those ideas have had on cognitive research over the last century. Neuroscientists and cognitive psychologists might be able to get away without that knowledge, but a cognitive scientist cannot.
Jair said,
May 28, 2010 @ 1:41 am
Peter,
You have a good point. I should have been a bit more clear – I didn't mean to imply that all mathematical developments are necessarily spurred by real-world problems. Often the problems involved are the purest of pure mathematics. Complex numbers, for example, were not developed to solve problems in engineering, but were developed in part due to the search for solutions of third- and fourth- degree polynomials.
I take your point that powerful mathematics can arise without specific applications. But I have a feeling most of them come from some hard thinking about good problems. To use one of your examples, think of Boolean algebra. I don't know much about the history of the subject, but I know it wasn't developed in isolation; as I understand it, Boole found a way to model logic using algebra. While he might not have had a particular problem in mind, he was connecting two subjects that before had been thought wildly disparate. His ideas didn't just spring fully-formed from his sole mind.
My point is that the crystalline presentations of some math books give the impression that math is formed when axioms fall from the sky and someone decides to start demonstrating their various consequences until something useful turns up. By tidying up all the messiness, they lose some of the flavor. I love it when authors go a little out of their way to provide some historical context for their subject.
maidhc said,
May 28, 2010 @ 2:34 am
I believe that Boole's work was fairly obscure until Claude Shannon showed that it could be used to analyze the operation of telephone switching circuits in 1937. Wikipedia (or actually William Poundstone) says "It has been claimed that this was the most important master's thesis of all time."
I remember a Dr. Who episode when they went to Bletchley Park during WWII, and Ace's knowledge of basic Boolean algebra was considered the equivalent of having a high security clearance.
I've often wondered whether mathematicians deliberately conceal the history of the development of probability theory because so much of it was to do with people trying to get rich by gambling.
I've sometimes been puzzled by students answering in the following way:
Q: Describe how a binary search can be used to find a given number in an ordered array of numbers.
A: Find the number using a binary search.
I suppose the answer could be that the student has no clue, but figures that by rephrasing the question he might pick up a point or two. But I still have a lingering doubt that someone somewhere is teaching that this is a legitimate way of answering a question.
Kragen Javier Sitaker said,
May 28, 2010 @ 3:50 am
maidhc: I wonder about that kind of answer too. Charitably, I wonder if the student has given up on understanding what the question is asking. After all, "Find the number using a binary search," is a perfectly reasonable answer to "How do I find a given number in an ordered array of numbers?" Clearly the question is asking for some kind of additional detail or context, since it already provides that answer, but it doesn't say what. It's obvious to me that the question is asking for some kind of walk-through of the steps of the algorithm, but without knowing more about the class it was being asked in, I wouldn't know whether to offer a Hoare-logic proof of its correctness, or a walkthrough for a particular case, or a vague outline of the algorithm as if I were trying to explain it to someone.
Perhaps some students don't even get to that point. I mean, there are lots of kinds of detail you could add to the picture. You wouldn't want to use binary search for an ordered list of numbers on tape, for example, or probably for an ordered list of numbers on a magnetic disk, or in a linked list, so an arguably valid answer would be, "It can be used efficiently when the numbers are in random-access memory." How would you implement this in practice? You'd be very likely to invoke bsearch or bisect or the equivalent from your standard library. When would you use an ordered list of numbers instead of, say, a hash table? Well, maybe when both membership testing and ordered enumeration need to be efficient.
Anyway, my point is, the question is pretty nonspecific about what kind of answer it's looking for.
Information Pioneers said,
May 28, 2010 @ 7:15 am
Thought you might be interested in this campaign from the BCS: http://pioneers.bcs.org/ – trying to raise the profile of pioneers such as Alan Turing. There are 5 films on the website now, the other pioneers are Ada Lovelace, Hedy Lamarr, Sir Tim Berners-Lee and Sir Clive Sinclair. If you get chance to have a look let me know what you think :o)
RadarLake » If math class were like English class… said,
May 28, 2010 @ 8:22 am
[…] blog about language from the University of Pennsylvania) with an interesting story about why engineers are so different from the rest of us. Well, it wasn't targeted specifically at engineers but I like to make fun of them because I […]
JimG said,
May 28, 2010 @ 8:51 am
> "If I know how to solve a problem,
> what does it matter whether I know
> who first figured it out?" She had assumed
> that the intellectual-history aspect of
> the lectures was a sort of non-nutritive filler, …
She was a budding cynic "who knows the price of everything and the value of nothing," according to the noclone (See
http://itre.cis.upenn.edu/~myl/languagelog/archives/002898.html )
or maybe just a blooming idiot. (Thanks to Groucho for this chestnut.)
Mr Punch said,
May 28, 2010 @ 9:55 am
James Bryant Conant, a chemist who was president of Harvard 1933-53, was deeply concerned about the "two cultures" issue; under his influence, not only was science (and the history of science) given more attention in the general education curriculum, but the history of each discipline was infused into science programs. The effects were certainly apparent, though perhaps waning, at least through the 1960s.
Troy S. said,
May 28, 2010 @ 10:35 am
I've often wondered what a math curriculum that presented topics in the chronological order of their discovery would be like. You'd have to teach integral calculus well before differential, for one interesting wrinkle.
Jason Eisner said,
May 28, 2010 @ 12:20 pm
@marie-lucie:
Another gear. Two gears are said to be engaged with each other if their teeth are sufficiently intermeshed that one can drive the other.
This is (for me at least) the metaphorical frame evoked by "engaging [one's mind] with the material." If a student has not engaged with the texts, concepts, or questions of the course, she may see the material spinning past or feel it bumping against her mind, but this superficial contact isn't enough to move her thoughts. She needs to get closer to the course material and allow the contours of individual ideas (teeth) to make contact with her own.
Search for the buzzphrase "student engagement," which is common in the U.S. Wikipedia says:
Besides "engaged in" and "engaged with," there is also "engaged to." I hear that 50 years ago there were many more engaged students in that sense. :-)
linguist.in.hiding said,
May 28, 2010 @ 8:34 pm
> Paul Graham has an interesting take on the situation.
Thank you Alex Fink! And there I was thinking Paul Graham was one of those interesting persons WHO KNEW WHAT THEY WERE TALKING ABOUT.
I immensely enjoyed the stuff about "stuff". But now, but now…
BTW, Blake. Any mention of Richard Feynman lowers your I.Q. a lot. I'm sure the Feynman would concur. Heck, I see Euler and Gauß there, too…
Ray Girvan said,
May 29, 2010 @ 10:29 am
Mr Punch: James Bryant Conant, a chemist … the history of each discipline was infused into science programs.
In the UK at school level, I recall the Nuffield Chemistry coursebooks being very good. For instance, the part on the periodic table went into some detail about the early attempts such as Döbereiner's triads and Newlands' Law of Octaves, as well as the anecdote about Thomas Midgley stinking of garlic when he was experimenting with diethyltelluride, so when travelling he would
marie-lucie said,
May 29, 2010 @ 12:02 pm
I've sometimes been puzzled by students answering in the following way:
Q: Describe how a binary search can be used to find a given number in an ordered array of numbers.
A: Find the number using a binary search.
I think that in many courses students are asked to "describe" something without getting examples of what a "description" is in the context of the discipline.
In teaching introductory linguistics, especially syntax, I find that most students use "describe" for a multitude of things (just about any word of a sentence can "describe" something, but that is not a useful concept in syntax), so that word becomes practically useless. I don't use it in my teaching and strongly discourage its use by my students (there are a number of more exact words, which I suggest depending on the case)). Perhaps in the example above the student understood "describe" to mean "rephrase in a simpler way" (not that the answer does that). Since this happens with so many students, it is probable that many high school teachers also use the verb in this same vague way.
marie-lucie said,
May 29, 2010 @ 12:10 pm
Jason Eisner,
Thank you for your detailed reply on "engage with". I had not thought about the gears with teeth "engaging with" each other. (But here again, the concrete sense involves two reciprocating partners).
David Cantor said,
May 30, 2010 @ 3:17 am
A required course in my university curriculum was titled "Third Culture Rhetoric," and contained about exactly what the title suggests. This was in Lyman Briggs College in Michigan State University, a unique program that urged hard-science and pure-math students into history of science and philosophy of science courses, and offered literature and humanities courses tailored to getting the hard-science types to raise their heads and look around at the world. The program still exists.
Peter Taylor said,
May 30, 2010 @ 1:12 pm
If you take the question literally that's about the only possible answer. It would be clearer for the question to ask "Describe the binary search algorithm for finding a given number in an ordered array of numbers"; or "Describe how a binary search finds a given number …" My personal preference for a phrasing would be to say precisely what you want: "Give pseudocode for the binary search algorithm to find a given number…"
John G said,
May 30, 2010 @ 7:59 pm
When I was an undergraduate in the last century, people in 'honours' courses were required to take a 'pass option' (not part of one's official grade but we had to get 50%) in something unrelated to our specialty. A lot of science students in their senior year took Philosophy of Science, expecting it to be easy if not fun, and it was not classified as a science course. Many of them had great difficulty understanding why the professor wanted to talk about 'false' theories of the past.
And that course had the label that might have suggested a broader inquiry than what people happened to believe in 1968. As a political economy student, I enjoyed it, though I didn't understand the science as much as my sceptical classmates.
@marie-lucie: I think one 'engages with' a text by treating it as a living set of ideas, with some history and some ability to produce (by the student's research) more or less right or at least persuasive answers. I understand that as more actively questioning the text than just 'in depth reading', though the latter could and perhaps should require 'engagement'.
I doubt that an 'engaged' reader would accept the right answer to the question 'why did Huck join Jim on the raft?' as being that Mark Twain wrote it that way. An engaged reader would, or at least could, treat the characters as having motives of real people in their situations, and trying to understand them. Different kinds of writing require different kinds of engagement, I suppose. And a different kind of engagement might allow us to ask why the author decided to have Huck join Jim, and another might not think the two questions are different – the unifying theme could be 'how did the author understand his character?'. An author controls the character more than that, though, since the plot is not dictated completely by the characters.
I now work for a public service that values 'employee engagement', not quite in the same sense as 'student engagement' mentioned earlier, but no doubt some relative of it. Do we love our work, appreciate its importance and try to achieve its purpose, not just go through the motions? (I suppose the union may wonder if this is just giving us the gears, to take us back to another reading…)
Jens Fiederer said,
June 11, 2010 @ 1:19 pm
@Cialan
> Who determines what is or isn't a valid question? If the instructor makes
> it clear (at the beginning of the course or while covering the particular
> topic) that less-conventionally-tested topics deemed relevant to the
> material will be included in the course and on examinations, and
> his/her department is fine with this idea, is it still not a valid question?
No….once the student has signed up for the course, it's a little late for the instructor to announce that it's really about something else. If, however, it had been made clear in the course description that this was not entirely a mathematics course, but included history of mathematics, it would be valid – but poorly titled.
If you signed up at a driving school, and your driving instructor told you as you got in the car that you were going to be taught and tested on how cars were invented and manufactured, you would be justified in being displeased.