Two Breakfast Experiments™: Literally
« previous post | next post »
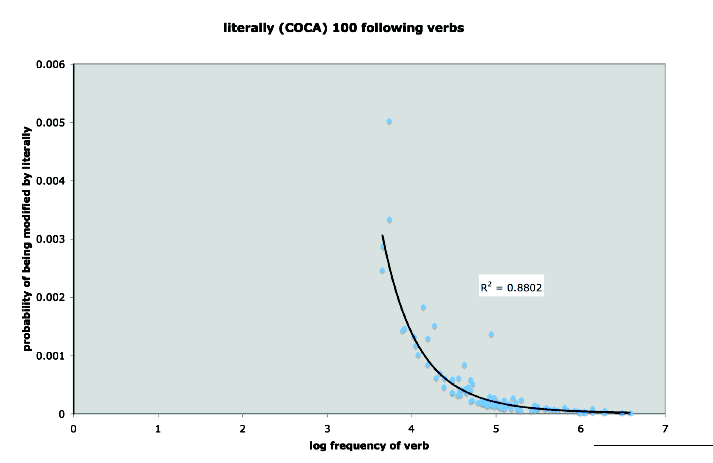
A couple of days ago, following up on Sunday's post about literally, Michael Ramscar sent me this fascinating graph:
What this shows us is a remarkably lawful relationship between the frequency of a verb and the probability of its being modified by literally, as revealed by counts from the 410-million-word COCA corpus. (The R2 value means that a verb's frequency accounts for 88% of the variance in its chances of being modified by literally.)
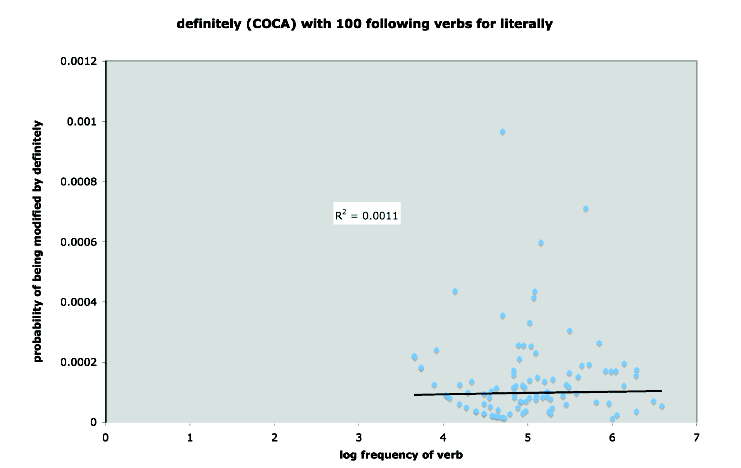
In order to persuade himself that this is not just some "weird property of small samples of language", Michael tried the same set of verbs with definitely:
As you can see, there's no sign of a similar relationship in this case — the shape of the empirical relationship is entirely different, and only 0.1% of the variance is accounted for.
Michael's accompanying note starts this way:
A couple of years ago I was playing around with the idea that representation had a cost — you couldn't learn to discriminate something efficiently without losing a certain sense of veridicality at the same time. I suspect that the loss of sensitivity to L2 phonological categories is a natural consequence of this (as is the loss of "perfect pitch").
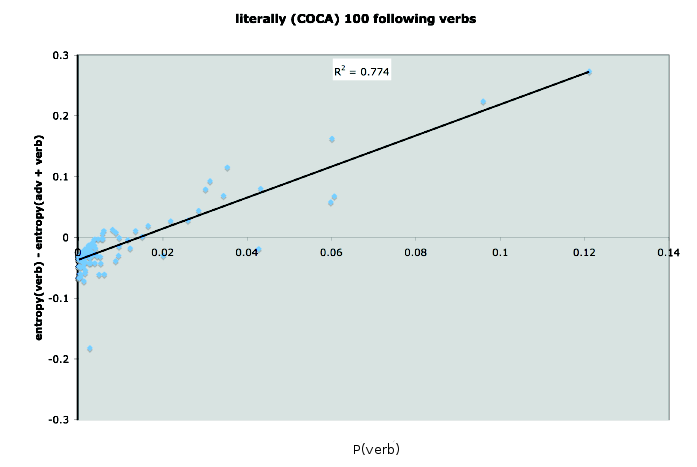
I began to think in the end that it was probably just the analog of physical principles of conservation (and that the only reason it wasn't obvious was because cognitive science is all about free lunches). — which is a long winded way of saying that i've been thinking more about "literally" as an intensifier, and what "intensifier" means. I think one can make sense of it in information theoretic terms. See the attached graphs, which show the probability that literally will precede a verb, plotted against the verb's log frequency, and then the change in the verb's entropy conditional on "literally."
As you can see, the way literally intensifies is to redistribute entropy. It makes lower frequency verbs more predictable (the counter-intuitive thing — because it is most "informative about highly informative verbs"), but it does this by making higher frequency verbs less predictable (the conservation bit) — which is also the part that sort of accords with normal linguistic intuitions, because in doing so, it makes higher frequency verbs more informative.
To control for the idea that this is a weird property of small samples of language, I've also plotted the distribution of the exact same set of verbs conditioned on "definitely" […] (if i wasn't needing to get on with the day, I'd do the reverse switch of definitely – literally too).
The graph that shows "the change in the verb's entropy conditional on literally" is here:
(Michael's graph labelled the x-axis as "p(noun)", which I'm pretty sure was a typo or something left over from another plot… apologies if I've misunderstood something.)
In a comment on Sunday's post, Dominik Lukeš linked to a post at Metaphor Hacker where he reports some other relevant corpus data about literally, "suggest[ing] that 'literally' is often associated with scalar concepts and therefore [functions] as both a potential trigger and disambiguator of hyperbole". Specifically, he notes that the top ten nouns immediately following literally (in COCA) are almost all quantificational:
- HUNDREDS 152
- THOUSANDS 118
- MILLIONS 55
- DOZENS 35
- BILLIONS 17
- HOURS 14
- SCORES 14
- MEANS 11
- TONS 11
And the top ten preceding adverbs also mostly suggest scalarity:
- QUITE 552
- ALMOST 117
- BOTH 91
- JUST 67
- TOO 50
- SO 38
- MORE 37
- VERY 31
- SOMETIMES 30
- NOW 26
Update — I asked Michael for the recipe that he used to create the plots. He responded:
hopefully this is better than a recipe… the actual spreadsheets i used to do the analyses. there is a lot of redundancy in them because this really was a breakfast expt, and os they are a hack / re-use of some tables that i made for adjectives and nouns. i've done a quick bit of coloring to help you make sense of them. the blue columns are the raw data, and the red columns are the ones that generate the graphs.
The spreadsheets that he sent are here and here and here. Some resulting plots are here.
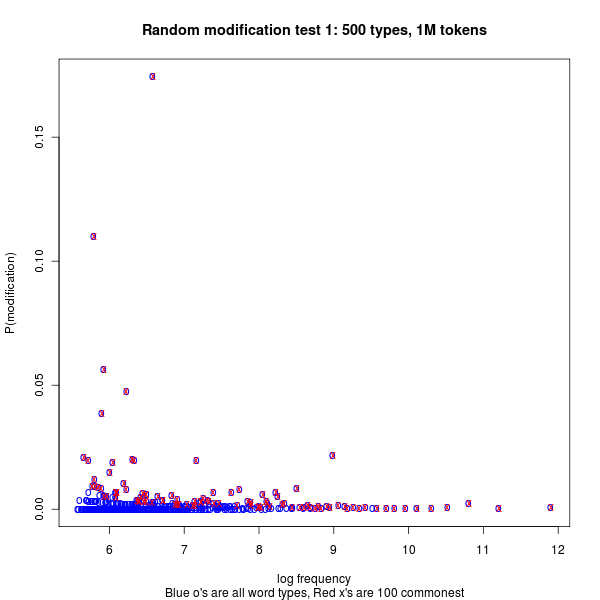
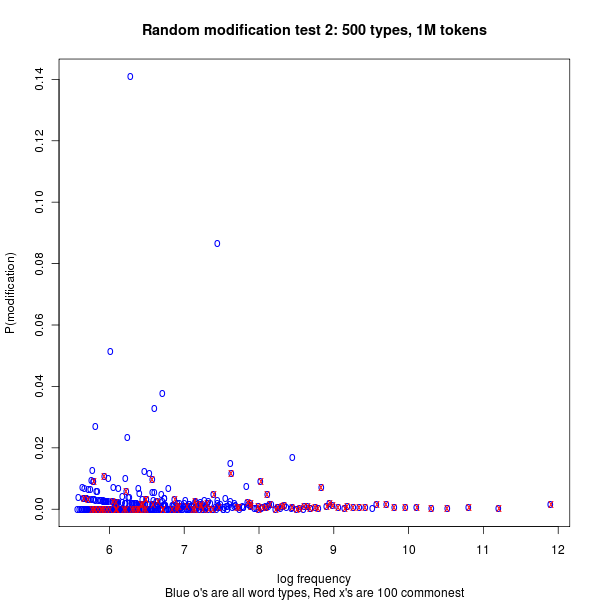
Update #2 — I think that Steve Kass is on to something about where the patterns come from, although I think the patterns themselves retain considerable interest. In order to check out his idea, I generated and plotted some fake data using this R script. The basic idea is to take a random sample of NTOKENS tokens from NTYPES types, assuming a 1/F probability distribution, and then to modify some of these randomly, by assuming an independent 1/F distribution of conditional probability of modification. We can then plot the log empirical frequency of types against the empirical probability of modification: the overall pattern shows a (noisy and quantized) version of the underlying distribution, and if we plot only the most-often-modified end of the list, we see the overall shape pretty well:
If show log frequency against empirical modification probability for counts derived from a second, independent probability-of-modification distribution, we see the same pattern overall, but the top of the list (being less fully determined by the things that determine the y-axis data) tends to sample the flatter part of the distribution:
It's possible that simulations more accurately reflecting the background facts of the COCA corpus would reproduce Michael's findings more exactly. But it's also possible that the patterns he saw deviate from these expectations — and in any case, his ruminations might apply even if the observed patterns are statistically necessary rather than linguistically contingent.
Brett R said,
March 8, 2011 @ 8:31 pm
Help! Michael's data looks really interesting, but I really can't make heads or tails of it. I've read it a number of times, and I just don't understand. Can somebody simplify or explain?
[(myl) The data behind the graphs is pretty straightforward. For the first graph, take the 100 verbs (verb lemmas?) that are most likely to occur following literally, and plot the log of their overall frequency in the corpus against their empirical probability of being modified by literally. The second graph is a more subtle presentation of essentially the same data.
Before I venture to try further exegesis, though, I'll see if I can get a more exact recipe from him, so that I can give an explanation that's correct as to the details (e.g. about whether "verb" means "verb form" or "lemma of verb forms" or what).]
Seth Johnson said,
March 8, 2011 @ 8:53 pm
My interpretation of the first graph is that the more common a word is, the less meaning it has on its own. (I'm not a linguist so I am ignorant of the more precise terms to use here.) Unusual words have connotations that are lost when the word is ubiquitous. Consider "awful" vs. "repugnant." Awful originally meant "causing terror or dread; appalling" (SOED) but it is commonly used to describe, for example, a boring meeting. It would make more sense that "awful" needs intensifying with a word such as "literally," whereas "repugnant" could stand on its own.
[(myl) Except that the first graph tells us that the commoner a verb is — the higher its (log) frequency — the less likely it is to be modified by literally…]
Rubrick said,
March 8, 2011 @ 9:16 pm
This is a brilliant bit of work.
Seth Johnson said,
March 8, 2011 @ 9:37 pm
@(myl) Sorry, I thought that was a negative log scale, as a fraction of words in the database, where the data points on the right occur less frequently than once per million words.
Ray Girvan said,
March 8, 2011 @ 9:43 pm
Extremely. And the COCA interface itself is worth exploring. It's late so I won't get embroiled in it now, but I'm wondering if it can be used to get stats on the use of "very" as an intensifier for 'extreme adjectives'. One of my little bêtes noires is the claim in a lot of ESL tutorials that you can't use constructs like "very ancient", "very fascinating" or "very tiny", which seems to go wildly against real usage.
Craig said,
March 8, 2011 @ 9:52 pm
I think that perhaps it still is a function of small sample sizes and an order of magnitude difference for the frequency of using a particular adverb–check the two y-axis scales on the probability versus frequency graphs. Also, the error inherent in any "measure" of probability, the empirical search of number of times modified over the number of times used modified or not, is such that in these small sample sizes i would seem that as a verb used less frequently would need fewer total modifications to effect the same "probability" of modification, that the data is still inconclusive. I doubt you could find an adverb using this technique that tends to score a higher probability the greater the frequency of the verb.
Steve Kass said,
March 8, 2011 @ 10:13 pm
Mark,
Somewhat like Brett, I can make little sense of the data, and for what it's worth, I have a Ph.D. in mathematics…
I think I know what's going on, and I think it’s an artefact. My guess, and if I have time, I‘ll try to work it out more carefully, is that Michael goofed right here:
What he should have done is try the same experiment with definitely. The 100 verbs in Michael‘s list were very special with respect to literally, and it‘s not surprising that they are not so special with respect to definitely (or any other adverb).
I suspect (and look forward to hearing more detail) that these are the top 100 verbs according to their overall frequency in COCA of appearing modified by literally.
If so, this list of 100 includes (over towards the log frequency 6-7 side), most of COCA’s common verbs ([BE], [HAVE], [SAY], …). These frequently appear modified by literally simply because they are so frequent. They aren’t especially often modified by literally relative to the average verb, but they got onto Michael’s verb list because they’re just common.
On the left side, with log frequency around 4, are some relatively rare verbs (10000 or fewer occurrences in COCA – putting them well below the top 100 verbs in overall frequency). These made Michael‘s list specifically because they are unusually likely to occur modified by literally. Thus their probability of being modified by literally is relatively high. Thus the curved plot.
When these same 100 verbs (as opposed to the 100 I think Michael should have picked – those most often appearing modified by definitely) are inspected for their likelihood of being modified by definitely, or probably most any adverb other than literally, they are suddenly unremarkable and all pretty much like any old verb. Hence the horizontal plot.
Just as one would expect, except perhaps if the two adverbs in question were literally interchangeable.
Steve
[(myl) I think that you're right, at least qualitatively — see Update #2 above. I'm much less certain that such effects are enough to produce exactly the results Michael found, including many patterns that I didn't write about. In any case the details of the patterns depend on the details of the underlying distributions involved, and therefore still may be of considerable interest.]
Bill said,
March 8, 2011 @ 10:26 pm
My interpretation is that the more common a verb is the ore likely it is to be used in a cliche, and the more of a cliche an expression is, the more likely a lazy writer is to use the word literally in the illusion that it will freshen up the expression.
To back of the snideness, this use of "literally" does depend on being paired with a cliche, even when it is well used. Some time ago someone here quoted, I believe from Jane Eyre, "here legs were literally shaking in her boots." The vividness here comes from the fact that this is a cliche, a meaningless string of words, which she may have used or heard a hundred times before — and here it comes to life, her legs really are vibrating.
Melody said,
March 8, 2011 @ 10:32 pm
Alright, I'm going to take a stab at translating this into something I can wrap my head around. If I understand right, Michael's saying that –
"Literally" increases entropy for high-frequency verbs, making them less predictable in context, but also more informative.
"Literally" does the opposite for low-frequency verbs – i.e., it decreases entropy and informativity – but this has the upshot of making low-frequency verbs more predictable in context.
So, the trade-off is that for high frequency verbs, "literally" is making them more informative; whereas for low frequency verbs, "literally" is giving us a processing advantage, by making them more predictable in context.
And then, the graph with "definitely" is showing that this pattern isn't 'promiscuous' – if we take the following distribution for "literally" and plot it against p(being followed by definitely) we get something else entirely. Which is to say that "literally" is, in some sense, optimized for its own distribution.
Did I get it? Do I win the big cash money prize?
Now I want to see the reverse plots for "definitely"!
Steve Kass said,
March 8, 2011 @ 10:34 pm
Here‘s an analogy that might make my previous hypothesis more believable.
Choose the 100 names most commonly given to African-American children. Names that are common in general, like John and Mary, will probably make the list because they are common. There are lots of African-Americans named John because there are lots of children named John. The percentage of African-American‘s with those names will not be much different than the percentage of all Americans (or Hispanics) with those names.
Near the bottom of the list, though, we might find names like Andre and Ebony, which would not be on the top 100 list overall, but which are among the top 100 African-American names because they are particularly common in that community.
If we now look at these 100 names (Ebony and Andre on the left of the graph, John and Mary on the right), and plot their log frequency as names in America against the probability that they indicate the nameholder‘s ethnicity as African-American, we‘ll get a curved plot.
Now look at the same 100 names and plot their frequency in America against the probability that they indicate the nameholder‘s ethnicity as Hispanic, we are more likely to get a non-curved plot, basically flat at the overall probability that a person is Hispanic. (Some non-flatness might show up if there are common naming patterns in the two communities, similar to what might occur because of the extent to which literally and definitely are somewhat interchangeable.)
Now if we chose the 100 most common Hispanic children‘s names and created the same plot, we would get a curve again.
Steve Kass said,
March 8, 2011 @ 10:45 pm
And regarding this remark:
This is not what the first graph tells us. The first graph tells us that among those verbs that most frequently appear modified by literally, the commoner ones are less likely to be modified by literally.
A graph cannot tell us something like “the commoner a verb is …” if it shows only a very special list of verbs.
If Michael had plotted all verbs appearing at least 5000 times in COCA, in addition to the points he did plot, we would see many additional points, and then the graph would allow us to say “the commoner a verb is … .” But most likely, we would get no striking conclusion. All of these additional points would represent verbs modified by literally less frequently than the ones we do see in the first graph, so the additional points would lie below the ones we see in the plot. The best fit curve through the full set of points would probably tell us that the commoner a verb is — well, nothing regarding its likelihood of being modified by literally…
Steve Kass said,
March 8, 2011 @ 11:44 pm
I see that Mark has now updated the post to include Michael’s spreadsheets. The leftmost points on (both) his graphs represent the following verbs:
ripped, exploded, translated, blown, blew, knocked, shaking, thrown, surrounded, saved, threw, dying, falling, killing, pushed, broke, shut, and fighting.
The COCA frequencies of these verbs fall between 4,454 and 30,000, far below the frequency of the 100th most common verb in COCA, which appears over 87,000 times. In other words, they appear in Michael‘s analysis because they are very special with respect to literally.
On the other end, the verbs appearing in Michael‘s data with COCA frequency above 1,000,000, are these.
has, were, had, do, have, are, be, was, and is.
Not surprisingly, they are the top 10 COCA verbs overall, regardless of proximity to literally, so they are not special with respect to literally.
Michael’s data supports the following hypothesis, to the extent that COCA
There is probably a name for the statistical paradox or fallacy when data is analysed in this way, but I can‘t find it. It seems close in flavor to Berkson‘s paradox, but not quite a match.
Steve
Steve Kass said,
March 8, 2011 @ 11:48 pm
… completing the incomplete sentence above: Michael’s data supports something like the following hypothesis, to the extent that COCA represents American English, but not a lot more I’m afraid: Moderately common verbs unusually likely to follow literally in American English are not distinguished with regard to their likelihood of following definitely.
R. Wright said,
March 9, 2011 @ 12:24 am
Wow, interesting pattern. I wonder if I could work this kind of apparent law into a college math lesson.
Richard Futrell said,
March 9, 2011 @ 1:06 am
I don't think the point is that verbs after "literally" have a special distribution as compared to verbs after "definitely". It's not special, as you point out. The interesting thing is that the more infrequent a verb is, the more likely it is to be modified with "literally". Which is cool because infrequent verbs are probably more specific and you'd think they need less 'modification'. Apparently, the role of "literally" is about prediction and information theory, not just meaning. Sure, the graphs only show this for verbs that have ever been preceded by "literally", but it's still an interesting point.
Tadeusz said,
March 9, 2011 @ 2:45 am
Lemmas? Or types?? I believe the latter.
I think Steve's interpretation is correct, I also understand the graphs this way.
Intuitively, those verbs that go with "literally" have something common, they all share a certain component of physicality, a physical activity, which, however, can be understood metaphorically. Hence the "literally" modifier.
And a little question: how do you measure whether a word is more or less informative?? Or is it another metaphor?? Or just simple reasoning:if something is more frequent, it is less informative?
taswegian said,
March 9, 2011 @ 4:42 am
Go back a step- how were the verbs selected?
Tadeusz said,
March 9, 2011 @ 4:58 am
"verbs that most frequently appear modified by literally"
army1987 said,
March 9, 2011 @ 5:47 am
I've opened the spreadsheet, and a number of the verb forms only occur after literally one or a handful of times; that makes for very poor statistics. At least, you'd need error bars ±√N.
army1987 said,
March 9, 2011 @ 6:21 am
Also, if there was an uncommon verb with a low probability of being preceded by literally, you would never find it in the corpus preceded by literally at all.
Eugene van der Pijll said,
March 9, 2011 @ 6:36 am
And Steve's point is that that conclusion is not supported by the data.
The shape of the distribution in the first graph can be explained entirely with a cut-off on the (absolute) number of occurrences of "literally VERB", because expressed as a percentage, that cut-off is higher for less frequent verbs.
Faldone said,
March 9, 2011 @ 7:37 am
OK. I think I understand what it's saying. Now all I have to do is figure out what it means.
richard howland-bolton said,
March 9, 2011 @ 7:45 am
I hope I didn't miss anything announcing the fact, but "resulting plots are" 404ing on me: they can't be found at http://languagelog.ldc.upenn.edu/nll/wp-admin/top5_50-4_250-4.pdf
[(myl) Fixed now.]
Mark F. said,
March 9, 2011 @ 9:50 am
I understand the initial plot, and I am willing to provisionally disregard Steve Kass' point for the sake of argument, but I'm having trouble with Michael Ramscar's analysis. It sounds like he is saying that "literally" makes rare words more predictable, thus reducing their information content and hence increasing the relative information content of more common words. That seems to fit his data, but it doesn't sound like my idea of "intensification".
Am I close?
Grep Agni said,
March 9, 2011 @ 10:42 am
I think Steve Kass is correct and the pattern is purely a result of biased data selection — the same thought jumped out at me, though he explains it better than I ever could. Smart people make weird mistakes all the time: a few weeks ago I had to convince an engineer that it isn't possible to siphon water to the top of a hill.
Paul Kay said,
March 9, 2011 @ 11:53 am
@Steve Kass. Am I right in concluding that you would say that if Michael Ramscar, had plotted against the likelihood of occurring after 'literally' the frequency of each of his 100 words divided by the frequency of the word's occurring in the corpus – instead of plotting its raw frequency, he would not have found the surprising relationship he found? The reason I ask is that if your answer is yes, it might be helpful to my fellow mathematical ignoramuses in understanding what's going on.
J. W. Brewer said,
March 9, 2011 @ 12:10 pm
A question on the separate corpus data from Dominik Lukeš: the list of following nouns is quite striking, but the list of preceding adverbs consists of adverbs that I would impressionistically expect to be reasonably commonly found (although not necessarily all top ten in that order or those proportions) preceding a wide range of adverbs. Is there some baseline data as to what the most common preceding adverbs are in ADVERB ADVERB strings that would enable one to see if "literally" is unusual in this regard?
Steve Kass said,
March 9, 2011 @ 1:07 pm
@Paul: I’m not sure what you’re asking (but under various possible meanings, I think I would not say what you are suggesting I would).
If you’re suggesting that Michael should have measured and plotted something else about these 100 verbs, and that had he, he would not have been misled to a wrong conclusion, that’s not the case. The issue is that he shouldn’t have restricted all his analyses to these particular 100 verbs. For the 100 verbs Michael studied, the relationships he found are real. If he had analysed the data differently and not found the relationships, it would not have been a good analysis.
The problem here is two-fold, but the problem is not that a false relationship was found — the relationship is real. One problem is that he generalized the relationship he found in a sample to a larger context that the sample didn’t represent unbiasedly. What Michael found suggests nothing about verbs in general, because he selected his sample of verbs for study based on a special property with respect to the modifier literally. The other problem is that this relationship is completely expected because of the way data is selected, so what he found doesn’t tell us anything. (The data he collected might well tell us interesting things under other analyses.)
What Michael found (the strong relationship in the first plot contrasted with none in the second plot) would occur for all sorts of randomly generated data with no inherent meaning. For example, generate a 100 million token corpus from a few thousand nonsense words with nonuniform frequency distribution (meaning make sure there are rare words, common words, and others in between). Now color each token in the corpus red, blue, and/or green using fixed small probabilities for each color. Color the tokens independently of the word they represent, using a random number generator.
In this case, one would find that among the top 100 words (assuming 100 is not too small or too large compared to the total number of distinct words in the corpus) selected by the number of red tokens of that word, that the ones of these 100 that occur less frequently in the larger corpus will have a highest probability of being red. If these same 100 words were subsequently investigated for their blueness, there would be no relationship between commonness and blueness. (I suspect that this relationship would hold for relatively wide variation of the parameters. That in itself may be a fascinating mathematical statistics question.)
Trying to address your question though — Michael’s x-axis was raw frequency in COCA. Is that different from what you describe as “the frequency of the word's occurring in the corpus”? If it’s not, then the division you ask about would always yield the number 1, and the plot would be meaningless and unable to discover a relationship between two variables.
What Michael plotted (probability vs. log frequency) was a reasonable relationship to investigate, and he could have equally well investigated the relationship between probability and frequency with other choices of frequency-derived measure on the x-axis: log (frequency), frequency, square root of frequency, etc. (so long as the measure increases with increasing frequency). Log frequency is most convenient given the particular data values here.
Sorry to go on so long, but statistics is often difficult and subtle to explain, and errors in statistics are even harder to explain than the concepts. I hope it helps to try explaining it in various (and with luck, all correct) ways.
Steve
Paul Kay said,
March 9, 2011 @ 1:31 pm
@Steve. Yes, of course. What I wrote was nonsense. His x-axis WAS frequency in the corpus. I somehow persuaded myself it was something different from that, and needed to be normalized for that. Sorry for taking up your and other readers' time. As Emily Latella was wont to say, "Never mind."
Steve Kass said,
March 9, 2011 @ 3:42 pm
Thanks for the very nice update and graphs, Mark. To my eyes, the red dots from your fake data reproduce Michael’s patterns very closely. I’m not sure what would constitute reproducing “Michael’s findings more exactly.”
My intuition is that these patterns will also be relatively robust to differences in the probability-of-modification distribution. Michael’s experiment absolutely guarantees that red dots are never below blue dots in the first graph, and the “spreading up” of dots on the left is a 1/sqrt(N) thing. The rarer a word in the corpus, the greater the expected deviation between the actual modification ratio seen in the corpus and the “true” ratio in the language or underlying population distribution. Presumably all the dots in both pictures that lie above about p=0.02 are where they are by chance variation within a small sample, not because those words had such an intrinsically high modification probability.
If I read your script and remarks correctly, you modeled Michael’s “modified by literally” and “modified by definitely” as varying by token with 1/f distributions independent of each other and of the distribution that gave the tokens’ frequency. I had in mind using independent and constant-across-tokens probabilities of modification, which I think (and might try to show) will give the same overall picture, the only clue being the existence of any “bumps” on the right-hand tail.
While it may be worth investigating the degree to which Michael’s results differ from what would be expected from random data with independent distributions, I worry that the very small numbers (as army1987 noted, many points represent a single example with modification) will limit what can be said. And while the specifics of the interesting linguistic hypotheses are beyond my expertise, I don’t see a good reason to limit the analysis to some small number of verbs most frequently modified by a particular adverb.
Chris Waters said,
March 9, 2011 @ 4:29 pm
To further emphasize the points raised by Steve Kass, I'd like to point out that, as Bill mentioned, "literally" is often used with clichés and common metaphors. These common phrases often preserve older or archaic meanings of words, and some of these words (archaic or not) may not naturally take an intensifier, since "literally" is usually not meant as an intensifier when coupled with clichés. This would readily explain a low correlation with "definitely".
To accurately analyze the use of "literally" as an intensifier, it seems to me that you would have to exclude instances where it's used to mean "not-figuratively". Unfortunately, in the absence of true AI, such categorization would probably require gargantuan amounts of manual labor. If only there were a way to harness the incredible power of peeving! :)
What might be interesting is to attack the problem from the other end. Look at words commonly associated with "definitely", and see how they chart when coupled with "literally". This would still suffer from the flaw Steve noted, but could be suggestive of—if nothing else—directions for further analysis.
Dominik Lukes said,
March 9, 2011 @ 4:36 pm
@J. W. Brewer: You are of course right. These are very common adverbs you would expect on that list. But if you run a comparison of the top 10 adverbial collocates of adverbs like: definitely, ironically, figuratively and literally, you will find (quite surprisingly, at least to me) that "literally" attracts scalar adverbs the most. Far more so than 'ironically'. Which is something I would not have expected. But much more digging is needed before we can really say what this means.
Craig said,
March 9, 2011 @ 6:07 pm
Lol I'd like to take credit for trying to say what Steve said, minus the pHD or a good ability to proofread late at night. But alas, thank you Steve for an explanation of why my gut feeling was right.
Bloix said,
March 10, 2011 @ 12:09 am
If Steve Kass is right wouldn't the reverse experiment show a mirror image pattern? Starting with the words most likely to follow the word definitely? Perhaps someone here is competent to do the work-
Steve Kass » Take (Some of) the Data and Run said,
March 10, 2011 @ 12:22 am
[…] I spent a good chunk of the last 24 hours at one of my favorite hangouts, Language Log. My reason for lingering was to pore over (in good company) some interesting graphs Mark Liberman had put up about the ever-controversial adverb “literally.” [Link: Two Breakfast Experiments™: Literally] […]
Steve Kass said,
March 10, 2011 @ 12:53 am
Readers interested in the statistical issue might enjoy this blog post, in which I provide a non-linguistic example (murder rate vs. city size) where the same kind of selection bias leads to a misleading conclusion that there is an inverse relationship between the variables.
Dan H said,
March 10, 2011 @ 7:23 am
I'm neither a linguist nor a statistician, but I'm actually not sure the findings in the original study are all that counter-intuitive.
I'm fairly sure nobody is assuming that the graph can be extrapolated back to zero, implying huge numbers of people saying things like "literally addition-polymerized" or "literally centrifuged" so what we have is a trend showing that the verbs most frequenly combined with "literally" are words which see less, rather than more, general use.
As a complete non-expert, my take on this would be that (by and large) common verbs describe common actions (or at least, actions that are commonly talked about) and you wouldn't expect these verbs to be commonly prefaced with "literally" because – well you don't normally say "I am literally wearing a hat" if you just want to express the fact that you are wearing a hat. I would expect a less common verb to describe an action that is less commonly talked about and, as a result, I would expect a greater proportion of uses of that verb to be metaphorical, and therefore I would expect more instances of that verb to be prefaced by "literally" either for disambiguation or for emphasis.
Sorry, that got rather longer than I'd intended.
a George said,
March 12, 2011 @ 5:02 am
— but we do need "literally", because for once you were wearing one of your hats and not merely speaking on behalf of one of your pressure groups
Ned Baker said,
March 25, 2011 @ 3:00 pm
So, I'm a non-linguist working my way through this post. I think I need a break for a Coca-Corpus.
Sadly, Jamie Redknapp is literally correct – Telegraph Blogs said,
October 12, 2012 @ 11:19 am
[…] is literally to feed among the lilies." There are many other examples, and I point you towards the ever-excellent Language Log and this lovely Slate article on the […]