Modeling repetitive behavior
« previous post | next post »
A recent conversation with Didier Demolin about animal vocalizations motivated me to return to a an issue discussed in "Finch linguistics", 7/15/2011. (See also "Markov's heart of darkness", 7/18/2011, "Non-Markovian yawp", 9/18/2011, and "The long get longer", 12/4/2013.)
The point is this: In modeling the structure of simple repetitive behavior, considerations from (traditional) formal language theory can obscure rather than clarify the issues. These threats to insight include the levels of the Chomsky-Schützenberger hierarchy, the "recursion" controversy, and so on.
What follows is an attempt at a simple illustrated explanation.
This all started with a elementary question. A zebra finch's song consists of a sequence of one or more "motifs", each of which is a stereotyped sequence of distinct "syllables".
Question: What is the distribution of motif repetitions?
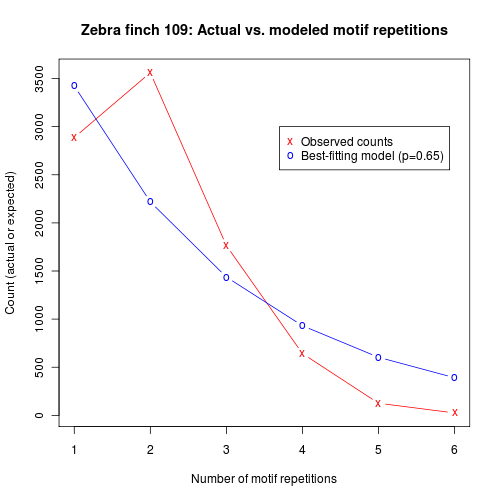
Answer: It looks like the red line in the figure below:
Why is this interesting? Because it suggests that the underlying process is not "Markovian", in the language of stochastic process theory, and that the "language" that it generates is therefore not "regular" or "finite state", in terms of the Chomsky-Schützenberger hierarchy.
How so? Here's how I explained it in the earlier post:
After producing a motif, our hypothetical markov process will be in a state where it must decide whether to stop or to produce another motif. By the markovian assumption ("history is bunk"), the probability of stopping will always be the same, regardless of how many motifs have been produced in the current bout.
Let Pstop denote this probability of stopping after a given motif. Then the the probability of producing a sequence of length 1 will be Pstop , the probability of producing a sequence of length 2 will be (1-Pstop)Pstop , and the probability of a sequence of length N will be (1-Pstop)N-1 Pstop . This implies that the modal number of motif repetitions will always be 1, and that the relative frequency of higher numbers of repetitions will fall off exponentially, at a rate determined by Pstop.
And in the figure above, the blue line represents the best-fitting exponential approximation to the observed distribution — which is clearly a qualitative mismatch to the facts.
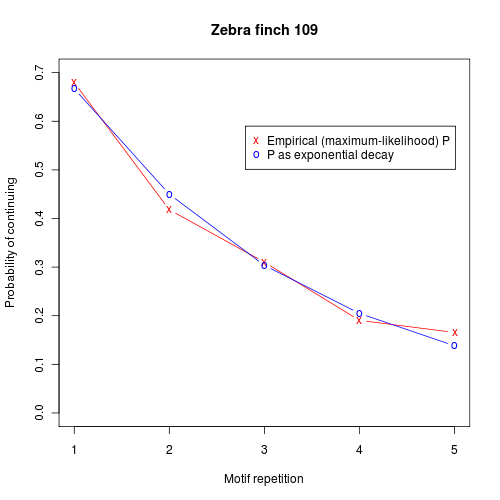
So what's happening? In statistical terms, it's pretty simple — the probability of adding another motif is an exponentially decreasing function of the number of motifs already produced:
Putting it even more simply, we might say that the bird is getting tired.
In slightly more formal terms, we might add to a simple two-state markov process a register representing "energy" or "activation" ; at each state transition, a bit of activation drains away; and the resulting activation level affects the probability of continuing the process.
It's easy to see how something like this might be implemented in neuromuscular terms. In fact, it's hard to imagine a realistic model of repetitive biological activity that DOESN'T have similar properties, at least in the sense of involving some sort of biochemical or neurological "memory" that causes gradual changes in a consistent direction over indeterminate sequence lengths. It wouldn't surprise me to find that some some bacterial behaviors work in a generally similar way.
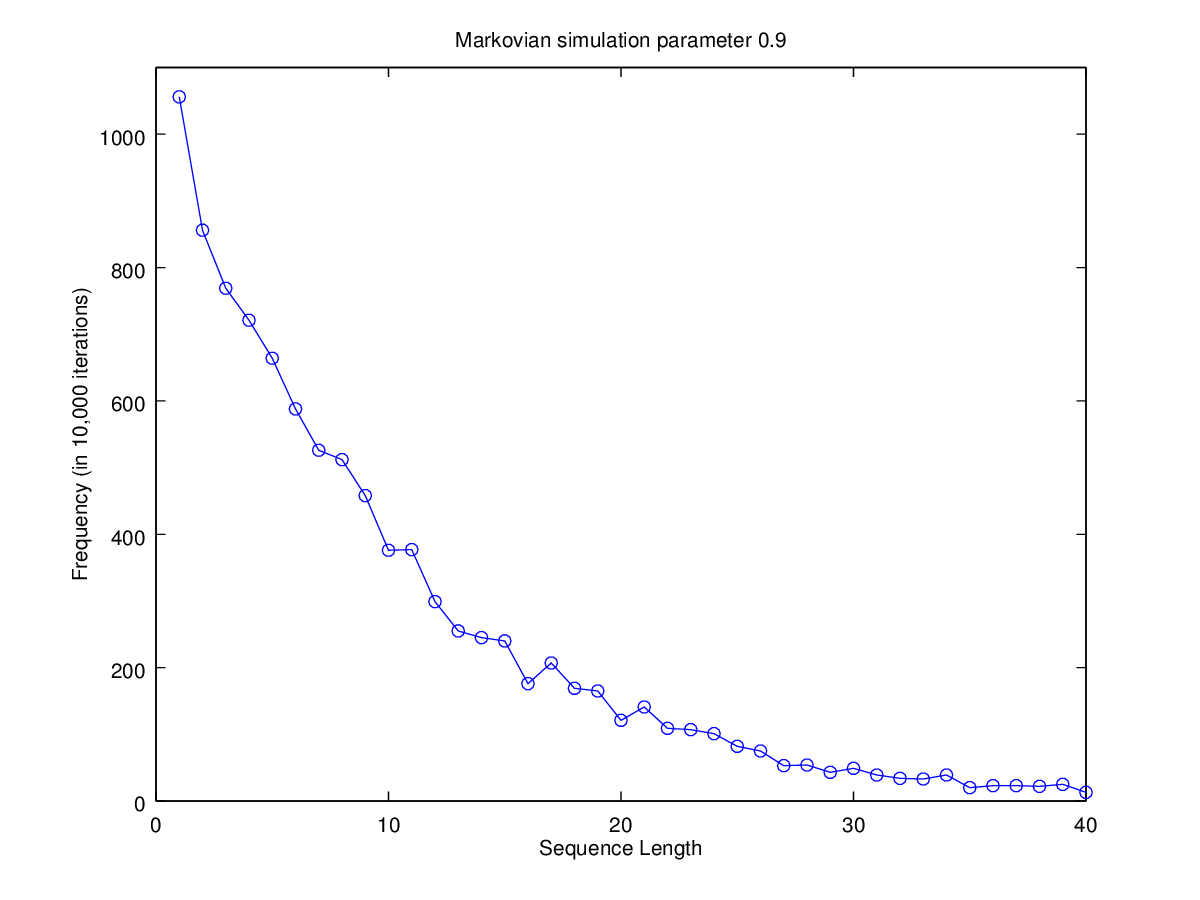
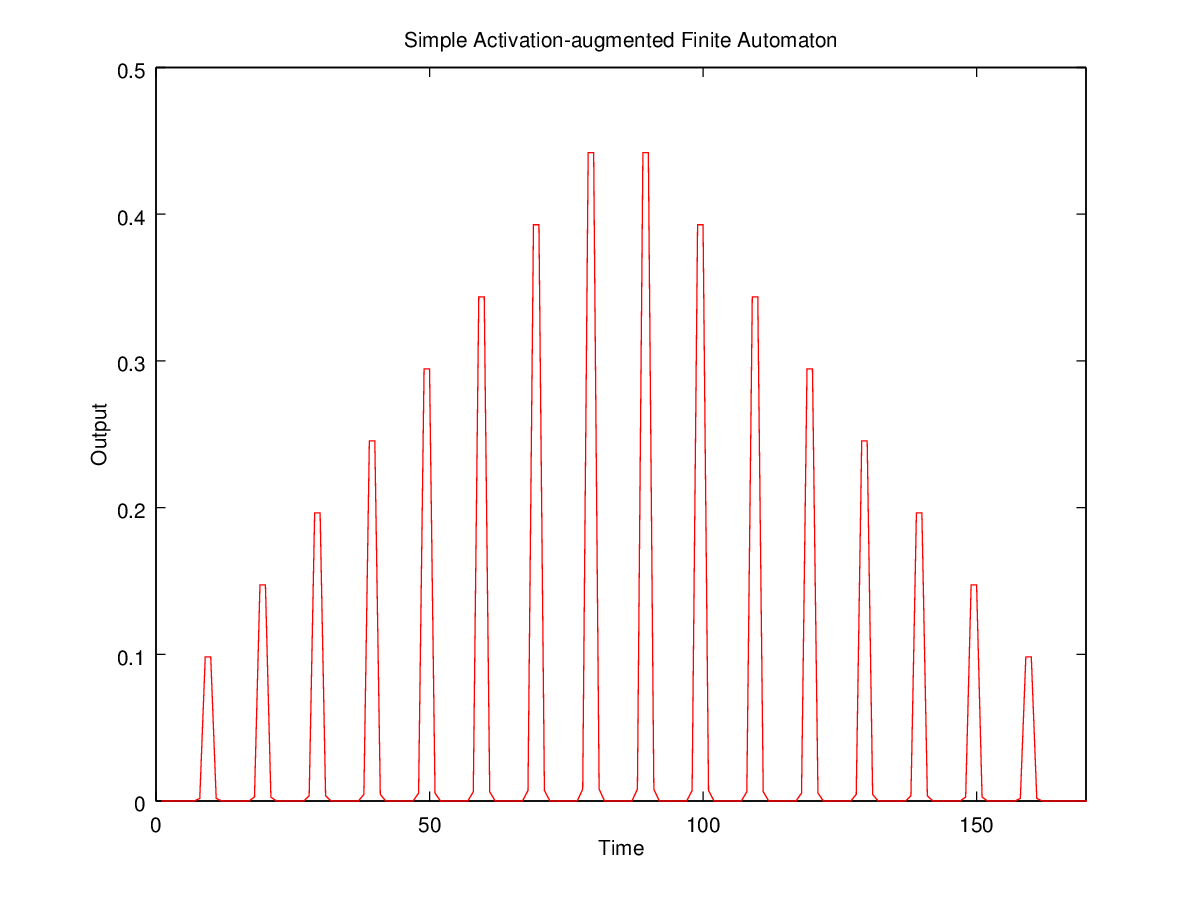
I won't try to prove the relevant theorem at this point, but here's a simple illustration-by-simulation. We start with a trivial two-state markov process, which starts in state 1 and stays there with probability P=0.9. Here's the distribution of initial state-1 string lengths for 10,000 trials:
The expected exponential length distribution emerges clearly.
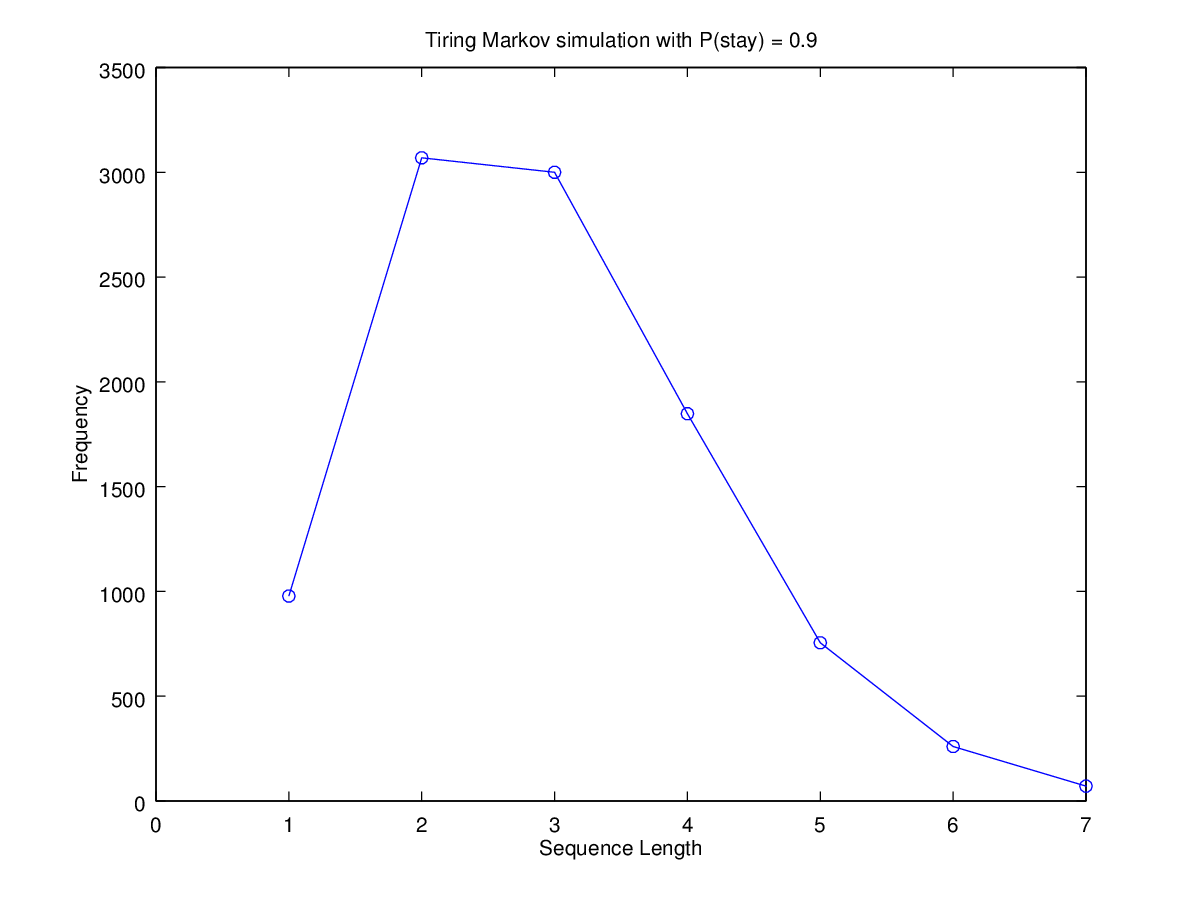
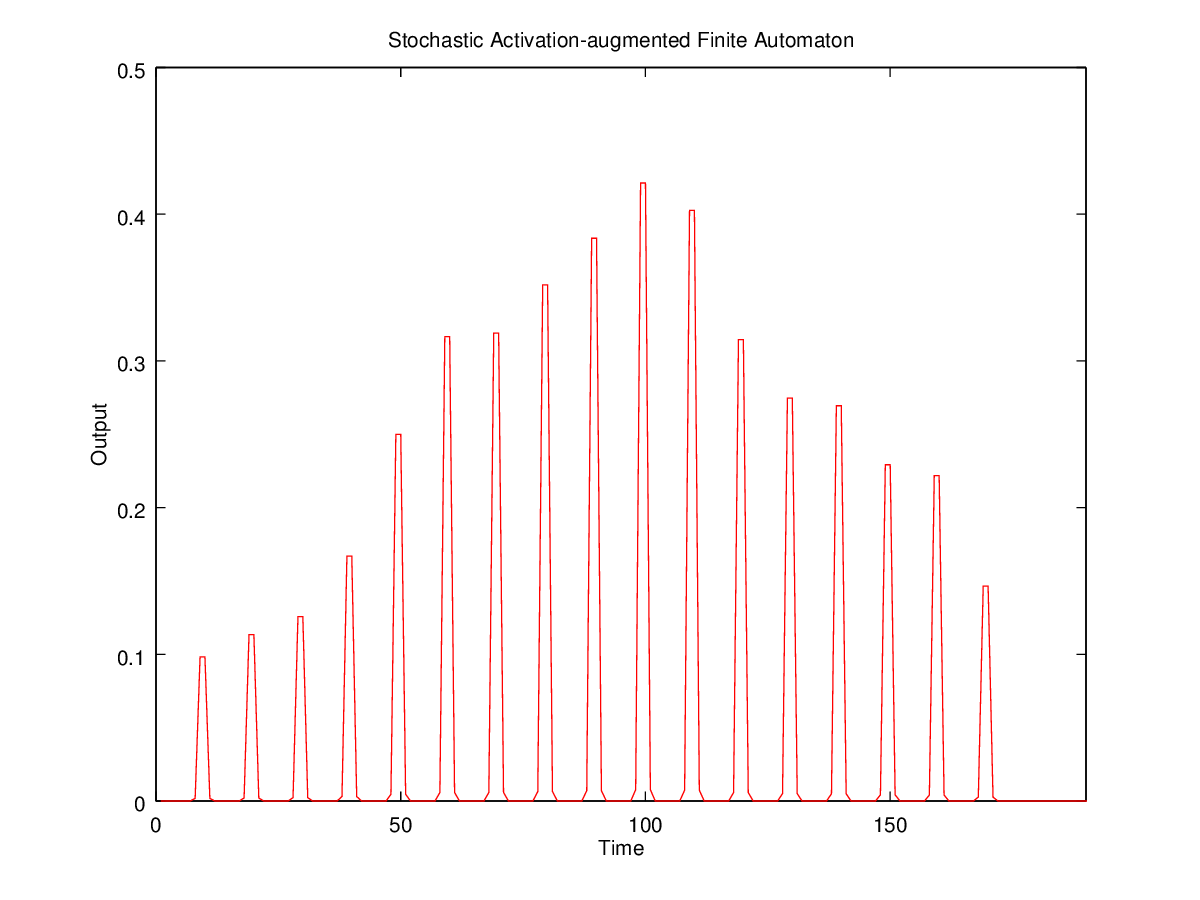
Now let's turn this into a "tiring markov process", by simply replacing our fixed probability of continuing in state 1 by a value that starts at 0.9 and decays exponentially towards 0.1 on each transition, by a factor of 0.7. The resulting distribution of lengths in 10,000 random trials is quite life-like, as it must be given the previous observations:
A bit of fiddling with the parameters would reproduce the observed distribution almost exactly.
The underlying process is transparently non-markovian, because the "activation" or "energy" level is acting as a sort of memory. This activation-level memory is part of the state of the system, and therefore the system as a whole has a potentially infinite number of states. But I hope it's clear that arguing about recursion and context-free grammars, in this context, is not a source of insight.
Still, it's absolutely true that adding a "memory" to a random process — even this very simple activation-level sort of memory — can lead to all sorts of interesting things.
Suppose that we shift to a "hidden" markov model, in which the observation sequence is a stochastic function of the state sequence. And suppose we allow our activation-level register to influence not only the state transitions but also the emitted values. Oh, and let's allow the activation level to be increased as well as decreased.
This vague sketch is consistent with lots of different formal details, which may or may not really matter to the resulting behavior. Leaving things vague for now, we can illustrate what this sort of system can do in a simple simulation.
There are three states — a "waxing" state, a "waning" state, and a stop state. We start in the waxing state, with probability 1 to remain there, and some low initial level of "activation". Each time we re-enter the waxing state we increase the activation level; and if that level passes a threshold, we transition to the waning state. We stay in the waning state, decreasing the activation level every time we re-enter it; and when the activation level falls below threshold, we exit to the stop state. At each step of the process, we emit the current activation level.
Obviously, what results is a sort of quantitative version of a Dyck (= balanced parentheses) language, consisting of sequences like the one shown in the figure below, where a rising series of levels is exactly matched by a subsequent falling series:
Or we could make the amount of increment or decrement a random variable, so that the rising and falling sequences are strictly monotonic but not necessarily exact mirror images:
And just a little more elaboration of our "activation-augmented hidden semi-markov model" will produce sequence-sets that would seem to require a "context sensitive grammar" if were to try to generate them with a model from the traditional grammatical hierarchy.
The point is not that mathematically modeling is irrelevant — on the contrary. Nor am I trying to argue that the patterns generated by processes of this kind are trivial or uninteresting.
Rather, the point is that some of the constructs of 1960s-era formal language theory, such as the Chomsky-Schützenberger hierarchy, can be a source of confusion rather than insight when applied to simple patterns generated by simple and biologically-plausible mechanisms. And the situation may not improve when we move on to more complex patterns.
Michael Watts said,
May 15, 2015 @ 5:01 am
If I were modeling breathing with this kind of setup, I'd start with parameters like "probability of stopping: 0 (regardless of activation level); energy drain per repetition: 0". Which isn't all that similar to having positive values for those numbers. I agree that breathing, as a repetitive biological activity, must drain energy in a physics-related sense, but not in the same sense that applies to, say, pushing a boulder up a hill, where you can get tired and stop.
[(myl) OK, breathing, heartbeats, etc. are different, in that they don't involve variably repeated activity separated by periods of non-action. But they have a similar aspect in terms of rate changes — exertion causes heartrate and breathing rates to go up gradually to some limiting value, and then to go down again gradually after the extra effort stops. That kind of sustained increase or decrease is again not well modeled by a memoryless process.
Gait is obviously different as well. So I should be more cautious in generalizing, but I think the fact remains that nearly all repetitive biological activities involve some kind(s) of biochemical or neurological "memory" that prevents them from being accurately modeled as purely markovian processes. (Or at least forces uninsightful multiplication of states with predictable parameters.]
David L said,
May 15, 2015 @ 9:40 am
Putting it even more simply, we might say that the bird is getting tired.
Tired, or bored?
That is, does the bird's repetitive signing cause it to become physically tired, or is it a behavioral thing? The bird's all like, I'm tweeting like crazy and no girls are showing up… Screw this.
In terms of the modeling this wouldn't necessarily make any difference, but it may be an interesting question for people who study animal behavior.
[(myl) Birdsong is pretty strenuous, I think — because it's intended as a fitness demonstration to attract mates, it showcases endurance as well as skill and group membership. But really, my point is just that it's easy to imagine common-sense quantities that can influence and be influenced by simple repetitive behaviors, and therefore play (to some extent) the role of a "memory" in automata-theoretic terms.]
David L said,
May 15, 2015 @ 9:41 am
Singing, I mean singing. But a lot of birds do sign too, in a manner of speaking.
D.O. said,
May 15, 2015 @ 2:11 pm
It is probably irrelevant to your larger argument, but what if we have a 3-state automaton? Then it's easy to organize the values such that the probability of continuing slides from the initial high value to the final low value in a logistic fashion. In other words, "tiredness" can be modeled as a discrete state rather than a continuum. At some point, of course, the difference becomes philosophical.
[(myl) I think this counts as "uninsightful multiplication of states with predictable parameters". Obviously one can generally create an arbitrarily-close approximation by encoding longer and longer histories into a larger state space, as Shannon proved in 1948.]
Which reminds me, we have had some back-and-forth sometime ago where you advocated the discrete approach (Calculus should be scraped) and I defended the continuous one (Calculus fits the nature).
Shimon Edelman said,
May 15, 2015 @ 2:35 pm
Another line of evidence for some non-Markov structure in what zebra finches learn from their tutors:
http://journal.frontiersin.org/article/10.3389/fpsyg.2015.00571/abstract
D.O. said,
May 15, 2015 @ 2:56 pm
Mr. Edelman, why non-Markov? From the paper: "All grammars had the form of a probabilistic first-order Markov graph specifying the transition probabilities among basic units."
Shimon Edelman said,
May 15, 2015 @ 2:59 pm
Non-first-order-Markov, I should have said (some of the models tested could learn collocations of basic units, which then served as units in their own right).
peterv said,
May 16, 2015 @ 1:51 am
"[(myl) Birdsong is pretty strenuous, I think — because it's intended as a fitness demonstration to attract mates"
Intended by whom? The bird might intend to attract mates, and thus sing. But I doubt the bird is intending to demonstrate fitness or any other quality. Indeed, these qualities are merely a conjectured explanation for the observed phenomena of singing followed by mating. Any intentions about such qualities are only in the minds of biologists, and they are neither present nor observable among the birds being studied.