The shape of a LibriVox phrase
« previous post | next post »
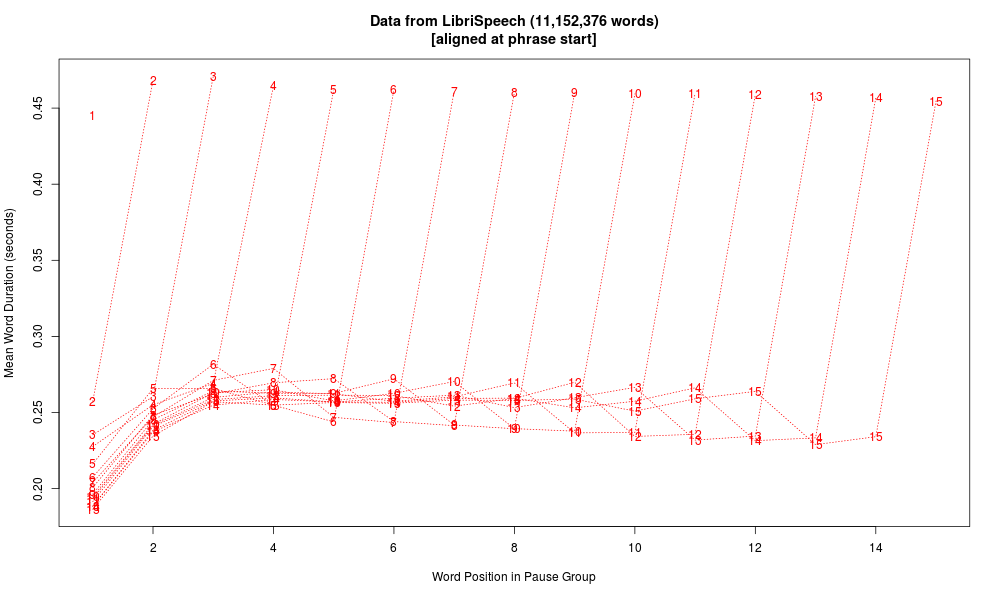
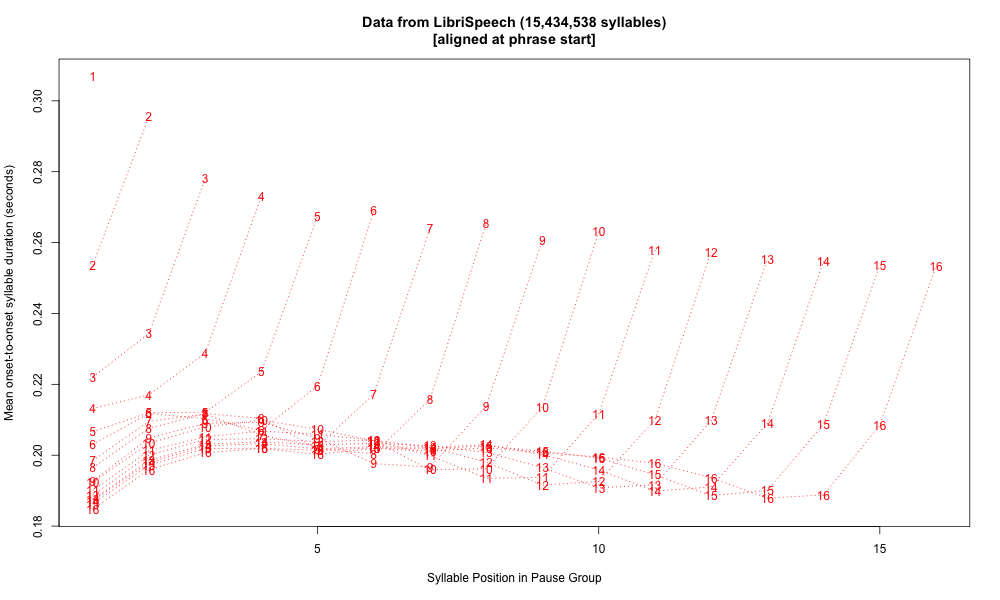
Here's what you get if you align 11 million words of English-language audiobooks with the associated texts, divide it all into phrases by breaking at silent pauses greater than 150 milliseconds, and average the word durations by position in phrases of lengths from one word to fifteen words:
The audiobook sample in this case comes from LibriSpeech (see Vassil Panayotov et al., "Librispeech: An ASR corpus based on public domain audio books", IEEE ICASSP 2015). Neville Ryant and I have been collecting and analyzing a variety of large-scale speech datasets (see e.g. "Large-scale analysis of Spanish /s/-lenition using audiobooks", ICA 2016; "Automatic Analysis of Phonetic Speech Style Dimensions", Interspeech 2016), and as part of that process, we've refactored and realigned the LibriSpeech sample, resulting in 5,832 English-language audiobook chapters from 2,484 readers, comprising 11,152,378 words of text and about 1,571 hours of audio. (This is a small percentage of the English-language data available from LibriVox, which is somewhere north of 50,000 hours of English audiobook at present.)
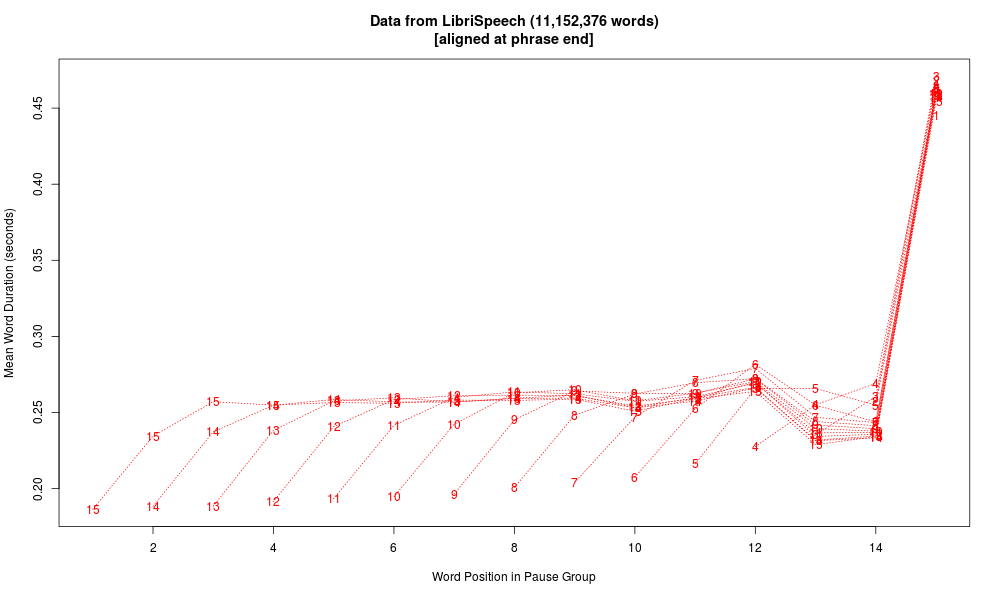
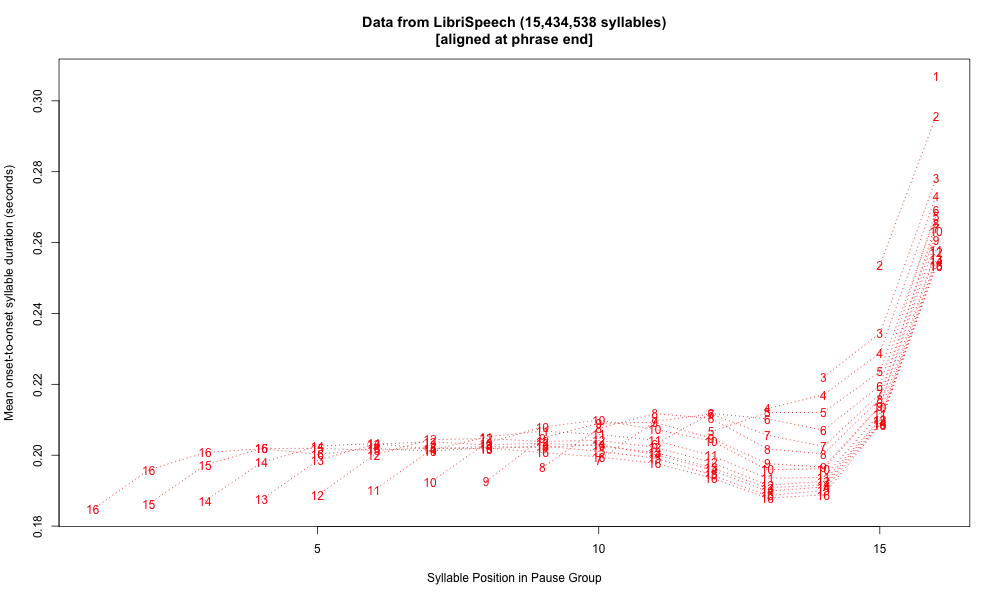
As a check on this process, I wrote a little script to divide our LibriSpeech dataset into pause groups and take the average of word durations by pause-group position, resulting in the graph above. Aligned at phrase ends rather than phrase starts, the same data looks like this:
There are some interesting similarities and differences with the analogous patterns in some other collections that I've looked at over the years:
"The shape of a spoken phrase", 4/12/2006
"The shape of a spoken phrase in Mandarin", 6/21/2014
"The shape of a spoken phrase in Spanish", 5/29/2015
But one consistent and unsurprising feature in all cases is the lengthening of pre-pausal words — the spoken equivalent of ritardando al fine.
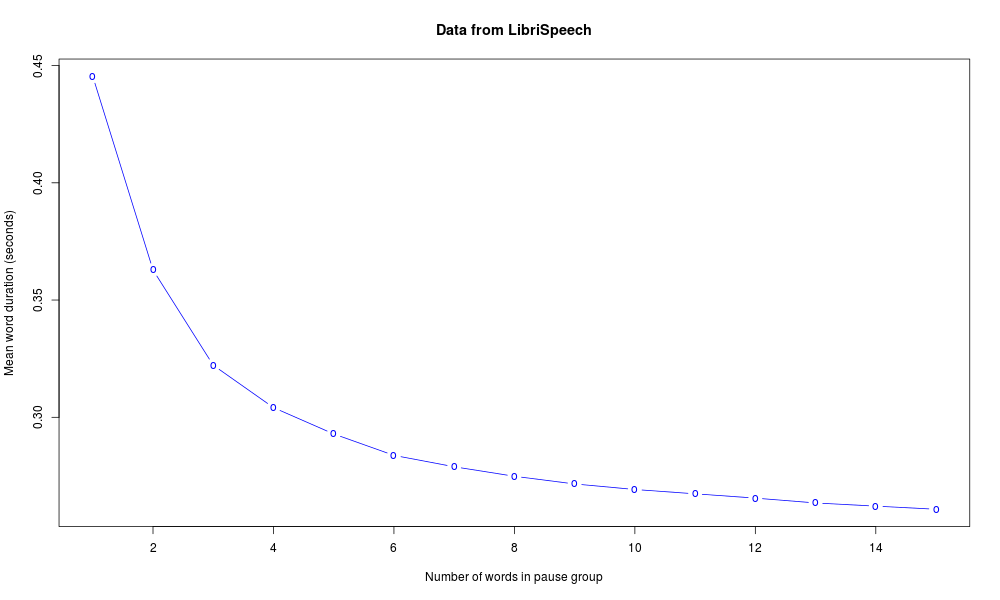
Because this final lengthening is (so to speak) amortized over different numbers of words or syllables in phrases of different lengths, average word durations depend systematically on phrase duration. Here's the plot of mean word duration as a function of phrase length in words, from this same LibriSpeech exercise — this dataset is large enough that the hyperbolic relationship shows up very nicely:
One important consequence is that you should be careful of using duration (of words, syllables, or segments) as an experimental variable, without taking account of the interaction with phrase length and phrase position. This is crucial if different subsets of your data have different distributions of phrase lengths, as is often the case.
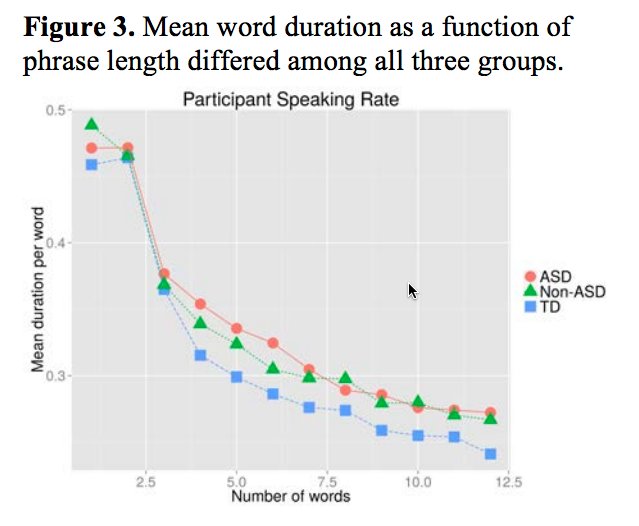
Here's an example from a recent workshop paper on the analysis of ADOS ("Autism Diagnostic Observation Schedule") interview segments (Julia Parish-Morris et al., "Exploring Autism Spectrum Disorders Using HLT", CLPsych 2016):
There are overall differences in mean word duration between the ASD ("Autism Spectrum Disorders") and TD ("Typically Developing") groups — but these differences could have been obscured (or exaggerated) by group differences in the distribution of phrase lengths.
Update — here are the syllable durations for the same dataset, calculated vowel-onset-to-vowel-onset for non-phrase-final syllables, and vowel-onset-to-silence-onset for phrase-final syllables:
Y said,
March 5, 2017 @ 12:00 pm
When you see differences in word duration, where does most of the variation come from? All vowels equally within a word? Final vowel? Continuant consonants?
[(myl) In the first place, it depends on the cause of the differences — overall speaking rate changes? pre-pausal lengthening? emphasis?
The relationship shown in the plots above is due to pre-pausal lengthening, and this is concentrated in the vocal gestures approaching the pause, mostly but not entirely in the final syllable. Exactly how it's distributed among the various (co-)articulations in the final syllable is somewhat complicated, but for a sense of the distribution across syllable positions, here's a comparable plot for the durations of the vowel (arpabet) /iy/ as in deed:
]
D.O. said,
March 5, 2017 @ 4:41 pm
Sorry for pedantry, but this is not an exponential relationship. It should be roughly a/(n+b).
[(myl) Assuming that non-final items have duration X and final items have duration (X+A), the mean duration of n items is (n*X+A)/n, or X + A/n. So you're right, the mean duration is decreasing hyperbolically (i.e. as 1/n) towards a value of X, not exponentially. In this context the empirical difference between exponential and hyperbolic decay is not very important, but I should name the concept correctly, so I've changed "exponential" to "hyperbolic" in the post…]
Of course, wherever there's mean there should be some measure of dispersion as well (and this is not about statistical significance at all), but of course, this is a blog post, not a paper.
[(myl) When N is in the millions, even small differences are often (statistically though not practically) significant. For example, for length=4 phrases, the means and standard errors of /iy/-vowel durations (as shown in this plot)
are (in milliseconds):
so that the std error bars are about the size of the plotting characters (and never mind that duration distributions are skewed — confidence-interval measures from other methods are similar.)
For all vowels taken together, the means and standard errors are:
In other words, sampling error is not an issue here. I agree that it's worth looking at quantiles for other reasons, though. ]
Another obvious observation, first word is short and in long phrases there is a slight decrease of duration for 2 words preceeding final. Any thoughts?
[(myl) This might be due to the fact that the distributions of words and word-types are not uniform across positions. Thus in English the frequency of determiners is probably greater in phrase-initial position compared to other positions, and determiners are short words.
On the other hand, a similar trend can be seen in the plot for durations of the vowel /iy/, as above. So a topic for further study.]
D.O. said,
March 5, 2017 @ 4:44 pm
Correction: the formula should be close to a/(n+b)+c.
D.O. said,
March 5, 2017 @ 5:02 pm
Should be about 0.246s/(n+0.231)+0.245s
D.O. said,
March 5, 2017 @ 5:06 pm
Probably, a bit of an overkill on my part 0.217s/n+0.248s is as good except n=1.
Charles Antaki said,
March 5, 2017 @ 6:04 pm
I wonder if the same pre-pausal lengthening would obtain in free conversation, and, more specifically, would be equally true before a) within-turn pauses, b) potential end-of turn pauses and c) actual ends of turns.
[(myl) See the 2006 post cited above, which was about conversational speech and included (for example) this plot:
]
It would be hard to do with large data sets, because the within vs potential-end-of turn vs actual end pauses would need hand-coding. My intuition would be that words would be lengthened where the speaker is likely to face competition for the floor, so roughly a = b > c.
Ryan said,
March 5, 2017 @ 6:41 pm
This seems less like a case of ritardando al fine and more like a case of fermata. Forgive my skepticism, but I don't see much evidence that this final lengthening is amortized over any number of words other than the last one.
[(myl) Don't forget that a word is not analogous to a musical note, but rather to a musical phrase — an average English word is made up of about a half a dozen sequential gestures — some are shorter, but some are much longer.]
Furthermore, because the final word works on such a different pattern than the other words in a phrase, I don't see the value in grouping it together with all the other words into a mean and saying that this mean decreases hyperbolically with phrase length.
[(myl) The whole point is that "mean word duration" — or "words per minute" or any other speaking rate metric — can be a problematic measure, in line with your objection (and also because the number and duration of pauses can vary). Sorry for not making this even clearer than it was.]
D.O. said,
March 6, 2017 @ 2:01 am
Yes, indeed, there is no first-word shortening in the switchboard corpus and there is no shortening of the penultimate word either. There is actually a slight increase. If these not very pronounced features differ from corpus to corpus it means that the reason is not very fundamental.
There is a bit of gender dimorphism too. I have run averages for the whole 98 switchboard corpus and separately for women and men. Here's the results. For phrases of duration 3 to 15 words average lengths of first to antepenultimate words is (they are similar throughout)
both genders: 225ms, women: 228ms, men: 222ms — basically no difference.
But for the last word
both genders: 383ms, women: 398ms, men: 368ms
Difference of 30ms is not very substantial, and, if viewed as a difference from the baseline is even less, +170ms for women vs. +146ms for men (~15%). Of course, I am not practicing my own preaching, no intervals etc. But it is just fun for me…