Nth Xest
« previous post | next post »
In the course of writing about the "fourth highest of five levels", I looked around at how the pattern "Nth Xest" is used in general. I found that uses of such expressions overwhelmingly count from the "top" where X names a top-oriented scale (high, big, long, etc.), and count from the "bottom" where X names a bottom-oriented scale (low, small, short, etc.) In other words, unsurprisingly, "Nth Xest" normally counts (up or down) from whatever end of the scale "Xest" names.
Another (less logically necessary but still unsurprising) thing I noticed is that top-oriented counts are always a lot bigger than corresponding bottom-oriented counts, and that counts decrease almost-proportionately as N increases. Thus from Google Books ngrams:
| second | third | fourth | fifth | sixth | |
| highest | 34447 | 9692 | 3148 | 1411 | 784 |
| lowest | 6006 | 1455 | 491 | 293 | 138 |
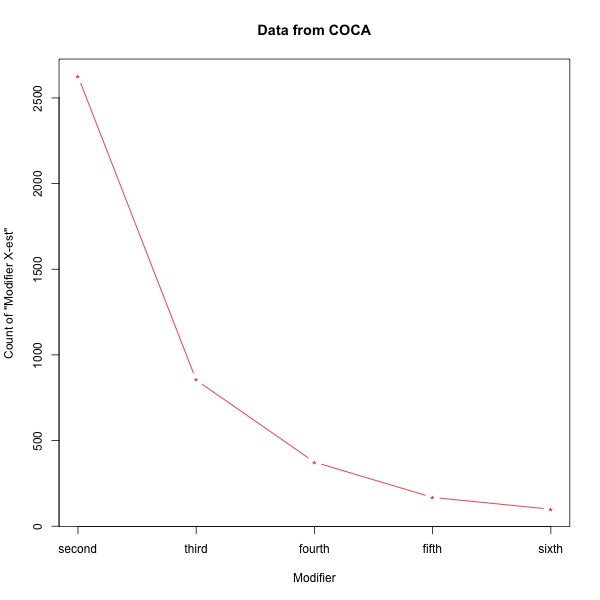
The numbers from COCA are pretty much in proportion, though lower:
| second | third | fourth | fifth | sixth | |
| highest | 305 | 95 | 33 | 23 | 12 |
| lowest | 55 | 9 | 4 | 3 | 2 |
Here are the Google Books counts for a larger set of values of X (values of 0 generally reflect cases where the count didn't reach the threshhold of 40 required for retention of ngram counts):
| second | third | fourth | fifth | sixth | |
| highest | 34447 | 9692 | 3148 | 1411 | 784 |
| lowest | 6006 | 1455 | 491 | 293 | 138 |
| biggest | 6001 | 1402 | 608 | 264 | 156 |
| largest | 124598 | 50022 | 20712 | 10595 | 6246 |
| greatest | 8333 | 1762 | 423 | 209 | 162 |
| smallest | 2703 | 605 | 200 | 92 | 49 |
| most | 114727 | 28723 | 8192 | 4028 | 2163 |
| least | 988 | 302 | 57 | 58 | 0 |
| best | 55695 | 7009 | 2337 | 649 | 426 |
| worst | 2417 | 501 | 142 | 95 | 0 |
| oldest | 14955 | 3041 | 661 | 202 | 128 |
| youngest | 2772 | 454 | 92 | 0 | 0 |
| longest | 3739 | 1660 | 713 | 412 | 171 |
| strongest | 3087 | 735 | 151 | 46 | 45 |
| richest | 1486 | 683 | 228 | 136 | 91 |
| poorest | 598 | 196 | 82 | 82 | 0 |
Adding them all up column-wise:
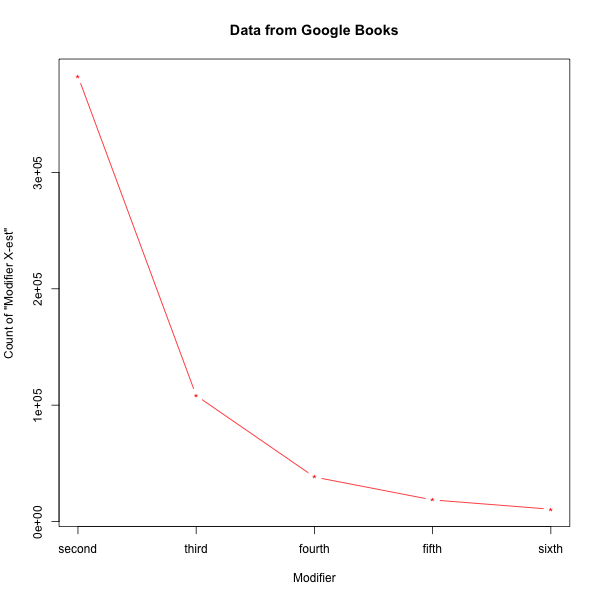
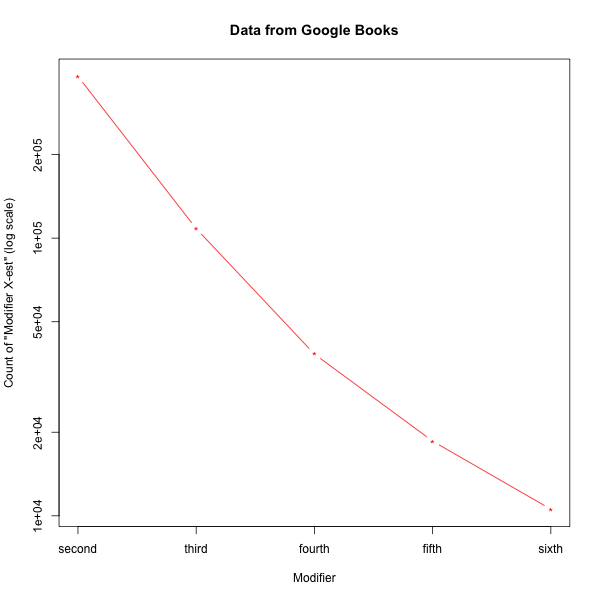
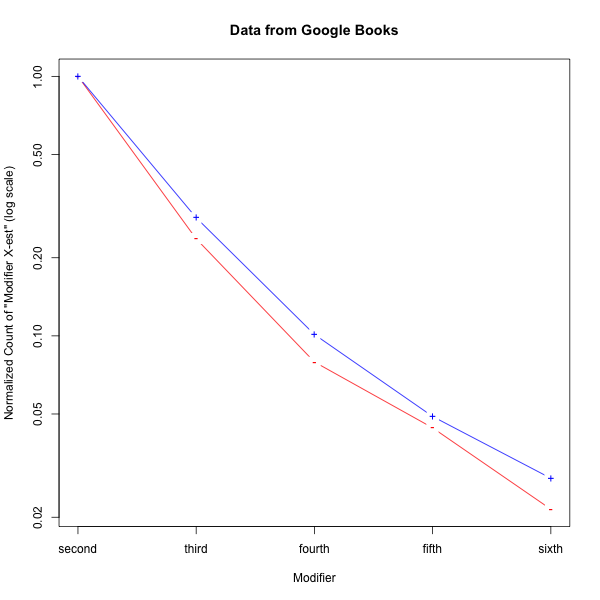
The left-hand figure below plots the counts on a log scale. And on the right, I've normalized the top-oriented and bottom-oriented counts, normalized by the count for "second Xest":
 |
 |
The same things for COCA counts:
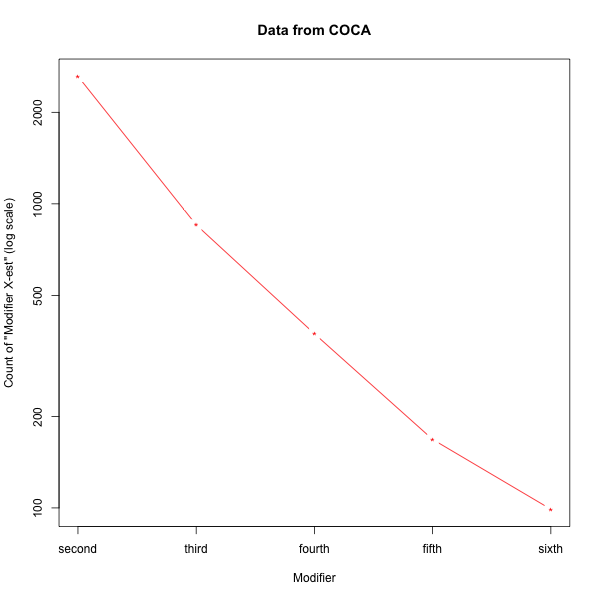 |
 |
It would be nice if the recently-developed distributional semantics methods could induce patterns of this type — but I don't think that they can do so yet.
D.O. said,
September 2, 2014 @ 11:51 am
Raw counts of the ordinal number words (without any coöcurrences) also show approximately exponential fall with somewhat diminishing exponent. Data from Google ngrams averaged for years 2000-2008 (they are really pretty stable over many decades) in words per million
first 815.7
second 264.4
third 130.5
fourth 36.3
fifth 21.9
sixth 13.3
seventh 10.7
eighth 8.8
ninth 6.5
tenth 7.8
I also included "first" which is not in Prof. Liberman counts for obvious reasons. Counts for "first" through "fourth" fall with exponent of 1 (that is, by the factor of e for any subsequent number), quite close to what happens with Nth Xest. So far, excluding the obvious case of the first Xest, there is no evidence that the use of ordinals with rankings is any different from the use of the ordinals overall.