Conditional entropy and the Indus Script
« previous post | next post »
A recent publication (Rajesh P. N. Rao, Nisha Yadav, Mayank N. Vahia, Hrishikesh Joglekar, R. Adhikari, and Iravatham Mahadevan, "Entropic Evidence for Linguistic Structure in the Indus Script", Science, published online 23 April 2009; also supporting online material) claims a breakthrough in understanding the nature of the symbols found in inscriptions from the Indus Valley Civilization.
Two major types of nonlinguistic systems are those that do not exhibit much sequential structure (“Type 1” systems) and those that follow rigid sequential order (“Type 2” systems). […] Linguistic systems tend to fall somewhere between these two extremes […] This flexibility can be quantified statistically using conditional entropy, which measures the amount of randomness in the choice of a token given a preceding token. […]
We computed the conditional entropies of five types of known natural linguistic systems […], four types of nonlinguistic systems […], and an artificially-created linguistic system […]. We compared these conditional entropies with the conditional entropy of Indus inscriptions from a well-known concordance of Indus texts.
We found that the conditional entropy of Indus inscriptions closely matches those of linguistic systems and remains far from nonlinguistic systems throughout the entire range of token set sizes.
More specifically, this paper represents an attempt to counter the arguments made in Steve Farmer, Richard Sproat, and Michael Witzel, "The Collapse of the Indus-Script Thesis: The Myth of a Literate Harappan Civilization", Electronic Journal of Vedic Studies 11(2): 19-57, 2004, discussed previously in Science by Andrew Lawler, "The Indus Script — Write or Wrong?", Science, 306(5704): 2026-2029, 2004.
Farmer et al. have already responded briefly, in Steve Farmer, Richard Sproat, and Michael Witzel, "A Refutation of the Claimed Refutation of the Nonlinguistic Nature of Indus Symbols: Invented Data Sets in the Statistical Paper of Rao et al."
The paper in Science on 23 April by Rao et al. was written in response to an article that the three of us published five years ago that has led to heated polemics over India’s oldest urban society. That paper argued that the short chains of symbols on Indus artifacts were not part of a writing system but of a simple nonlinguistic sign system of a type common in the ancient world. The vision of a nonliterate Indus society has solved a number of puzzles and now has many adherents, but it has also awakened resistance from Indian nationalists and researchers whose entire careers have been linked to the Indus-script thesis, one of whom is listed as a coauthor of this study. […]
Conditional entropy is not and has never before been claimed to be a statistical measure of whether or not a sign system is linguistic or nonlinguistic. Rao et al. only make it appear to be relevant to that end (as we find only in their online Supplemental Information section, but not in their paper itself) by inventing fictional sets of nonlinguistic systems that correspond (pace their claims) to nothing remotely resembling any ancient symbol system. If the paper had been properly peer reviewed it would not have been published.
Strong words. But if you read the papers involved, and understand the concepts, you should come to agree that Rao et al.'s convincing-looking Fig 1A (shown below) is indeed pretty much irrelevant to the question being addressed.
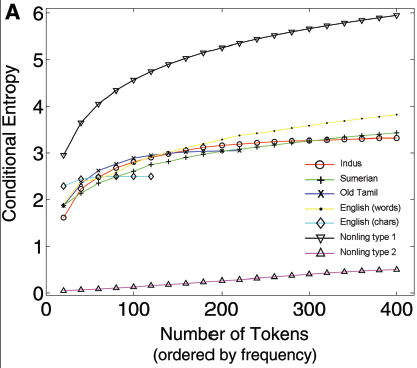
(If you're following the play at home, note that all the conditional entropies are in nats, and all are determined relative to just one preceding character. I couldn't find a clear explanation of the "number of tokens" on the x-axis, but it appears to mean that they estimated the average conditional entropy of the choices following the symbols that occurred 0-20 times in a corpus, 20-40 times, 40-60 times, etc. The gradual increase in estimated average entropy is then presumably due to the fact that the following-symbol distribution for the less-frequent cases is increasingly undersampled. )
[Update: No, according to a message from Rajesh Rao forwarded by Richard Sproat, this is *not* what the x-axis in that plot means. Rather, for each point n, the conditional entropy was re-computed based on the transition matrix limited to the n most frequent signs in the corpus. See the simulations below.]
That's all that I have time for this morning, but I'll come back to this topic later.
For now, I'll only register a small complaint about the lede in the story "Artificial Intelligence Cracks 4,000-Year-Old Mystery", Wired, 4/23/2009:
An ancient script that's defied generations of archaeologists has yielded some of its secrets to artificially intelligent computers.
To call a program that counts bigrams and calculates conditional entropy an "artificially intelligent computer" is … Well, you'll see.
[Since this is a topic that traditionally generates more heat than light, I've left comments closed. However, if you have something to say about it, write me and I'll add your thoughts as an update. ]
[Update 4/29/2009: In addition to the material below, see Cosma Shalizi's discussion here.]
[Update #1, 4/26/2009: It seems to me that their Fig. 1 is especially unconvincing, since a random process that made random bernoulli choices from an underlying distribution with uncertainty equivalent to about 20 equally-probable alternatives would show a similar average estimated entropy (conditional or not), asymptoting to about 3 nats as the sample size increases. It's true that their Table S1 shows that the bigram entropy for the Indus symbols is lower than the unigram entropy — but a "topic model" (e.g. a hidden markov model drawing from different symbol-distributions when it's in different hidden states, and switching states relatively infrequently, as if to model the construction of different inscriptions for different purposes or dedicated to different gods) would accomplish this just as well as a quasi-syntactic system would.
When I have a few minutes, I'll link to the code for a simulation showing this.
Fernando Pereira nails it, alas:
Once again, Science falls for a glib magic formula that purports to answer a question about language. They would not, I hope, fall for a similar hypothesis in biology. They would, I hope, be skeptical that a simple formula could account for the complex interactions within an evolutionarily built system. But somehow it escapes them that language is such a system, as are other culturally constructed symbol systems, carrying lots of specific information that cannot be captured by a single statistic.
]
[Update #2, 4/26/2009:(Removed because it was based on a misunderstanding of the X-axis in Rao et al.'s Figure 1A — see below for a corrected version…)
Again, this doesn't prove anything one way or another about the Indus inscriptions — it's just an attempt to refute by example the claim that numbers in Rao's Fig. 1 bear in any way on the hypothesis that the inscriptions represent a writing system. ]
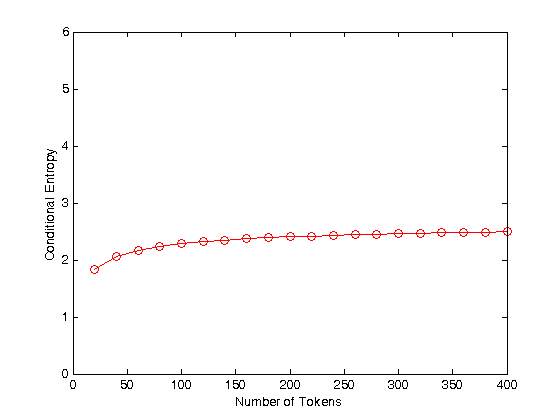
[Update 3, 4/27/2009: OK, I've learned that my analysis of the x-axis of Fig 1A was wrong. The truth is that for each point n, the conditional entropy was re-computed based on the transition matrix limited to the n most frequent signs in the corpus. So I redid things this way.
Just for fun, this time, I used a Zipf's-Law (1/F) type of frequency distribution rather than a negative binomial as in the previous (deleted) attempt. But again, I generated fake data using a random process without memory, so that (the expectation of) its conditional entropy values will be exactly the same as its unconditioned entropy. The Matlab code is here, and the resulting graph, again, has values that would fit well into the middle group of Fig 1A:
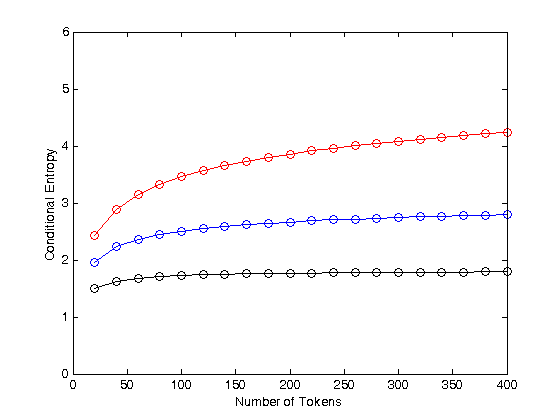
Again, this simulation matches the values in Fig 1A using a unigram model, without any sequential constraints at all. And if you want a different asymptote, just change the parameters of the simple, non-linguistic urn model that I used to generate the sequences. For example, the power-law exponent in the simulation code used for the graph above was 1.7 — below are the results for 1.1 (red) 1.5 (blue) and 1.9 (black).
And again, there are lots of easy ways to get a difference between different-order n-gram entropies without assuming that the underlying process is anything like a writing system, as I'll explain some other morning, if there's interest.
So again, I remain deeply puzzled about the relevance of Fig 1A to the evaluation of the Indus Script hypothesis.
Meanwhile, within a few minutes of posting this, I got email from Cosma Shalizi and Richard Sproat with their own simulations. Cosma stuck to a geometric distribution as in my original (now deleted) example, and wrote:
The entropy here is just the negative log likelihood of the estimated Markov chain divided by the sequence length. (I happened to have Markov-chain estimating code which calculated the likelihood.) It's the MLE of the transition probabilities, not their smoothed estimator, but that shouldn't make a huge difference.
A pdf of Cosma's results is here. Richard Sproat wrote:
I get a very good fit to their results for the Indus corpus with a model that has 400 elements with a perfect Zipf distribution, with alpha=1.5, and conditional independence for the bigrams.
Richard's Python code is here, and the resulting graph is here. ]