High-entropy speech recognition, automatic and otherwise
« previous post | next post »
Regular readers of LL know that I've always been a partisan of automatic speech recognition technology, defending it against unfair attacks on its performance, as in the case of "ASR Elevator" (11/14/2010). But Chin-Hui Lee recently showed me the results of an interesting little experiment that he did with his student I-Fan Chen, which suggests a fair (or at least plausible) critique of the currently-dominant ASR paradigm. His interpretation, as I understand it, is that ASR technology has taken a wrong turn, or more precisely, has failed to explore adequately some important paths that it bypassed on the way to its current success.
In order to understand the experiment, you have to know a little something about how automatic speech recognition works. If you already know this stuff, you can skip the next few paragraphs. And if you want a deeper understanding, you can go off and read (say) Larry Rabiner's HMM tutorial, or some of the material available on the Wikipedia page.
Basically, we've got speech, and we want text. (This version of the problem is sometimes called "speech to text" (STT), to distinguish it from systems that derive meanings or some other representation besides standard text.) The algorithm for turning speech into text is a probabilistic one: we have a speech signal S, and for each hypothesis H about the corresponding text, we want to evaluate the conditional probability of H given S; and all (?) we need to do is to find the H for which P(H|S) is highest.
We solve this problem by applying Bayes' Theorem, which in this case tells us that
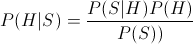
Since P(S), the probability of the speech signal, is the same for all hypotheses H about the corresponding text, we can ignore the denominator, so that the quantity we want to maximize becomes
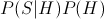
This expression has two parts: P(S|H), the probability of the speech signal given the hypothesized text; and P(H), the a priori probability of the hypothesized text. In the parlance of the field, the term P(S|H) is called the "acoustic model", and the term P(H) is called the "language model". The standard implementation of the P(S|H) term is a so-called "Hidden Markov Model" (HMM), and the standard implementation of the P(H) term is an "n-gram language model". (We're ignoring many details here, such as how to find the word sequence that actually maximizes this expression — again, see some of the cited references if you want to know more.)
It's well known that large-vocabulary continuous speech recognition is heavily dependent on the "language model" — which is entirely independent of the spoken input, representing simply an estimate of how likely the speaker is to say whatever. This is because simple n-gram language models massively reduce our uncertainty about what word was said next.
We can see this Lee and Chen's experiment, which looked at the effect of varying the language-model component of a recognizer, while keeping the same acoustic models and the same training and testing materials. (For those skilled in the art, they used the classic WSJ0 SI84 training data, and the Nov92 Hub2-C1 5K test set, described at greater length in David S. Pallett et al., "1993 Benchmark Tests for the ARPA Spoken Language Program", and Francis Kubala et al., "The Hub and Spoke Paradigm for CSR Evaluation", both from the Proceedings of the Spoken Language Technology Workshop: March 6-8, 1994.)
| Cross-entropy | Perplexity | Word Error Rate | |
| 3-gram Language Model | 5.87 | 58 | 5.1% |
| 2-gram Language Model | 6.78 | 110 | 7.4% |
| 1-gram Language Model | 9.53 | 742 | 32.8% |
| No Language Model | 12.28 | 4987 | 69.2% |
Thus using a 3-gram language model, where the probability of a given word is conditioned on the two preceding words, yielded a 5.1% word error rate; a 2-gram language model, where a word's probability is conditioned on the previous word, yielded a 7.4% WER; a 1-gram language model, where just the various unconditioned probabilities of words were used, yielded a 32.8% error rate; and with no language model at all, so that every item in the 5,000-word vocabulary is equally likely in all positions, gave a whopping 69.2% WER.
The 3-gram language model allows such a low error rate because it leaves us with relatively little uncertainty about the identity of the next word. In the particular dataset used for this experiment, the resulting 3-gram perplexity was about 58, meaning that (after seeing two words) there was as much left to be learned about the next word as if there were a vocabulary of 58 words all equally likely to occur — despite the fact that the actual vocabulary was about 5,000 words. (The dataset involved a selection of sentences from stories published in the Wall Street Journal, taking only those sentences made up of the commonest 5,000 words.)
The bigram perplexity was about 110, and the unigram perplexity about 742. (If you want to know more about such numbers and how they are calculated, look at the documentation for the SRI language modeling toolkit, which was actually used to generate them.)
If we take the log to the base 2 of these perplexities, we get the corresponding entropy, measured in bits.
And there's an interestingly linear relationship between the entropies of the language models used and the logit of the resulting WER (i.e. log(WER/(1-WER))):
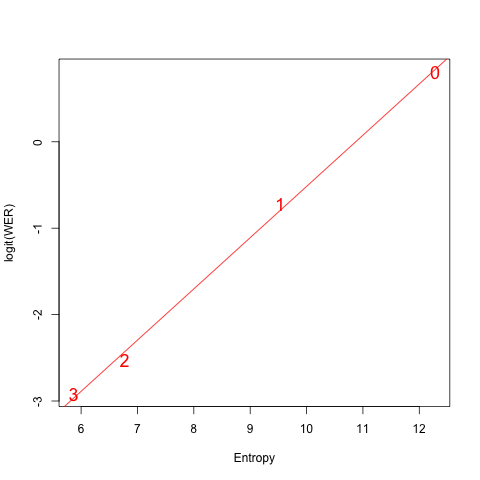
A different acoustic-model component would have somewhat different performance — the best reported results with the same trigram and bigram models on this dataset are somewhat better — but the overall relationship between entropy and error rate will remain the same, and performance on high-entropy speech recognition tasks will be poor, even with careful speech and good acoustic conditions.
This all seems reasonable enough — so why does Chin think that there's a problem? Well, there's good reason to think that human performance on high-entropy speech recognition tasks can sometimes remain pretty good.
Thus George R. Doddington and Barbara M. Hydrick, “High performance speaker‐independent word recognition”, J. Acoust. Soc. Am. 64(S1) 1978:
Speaker‐independent recognition of words spoken in isolation was performed using a very large vocabulary of over 26 000 words taken from the “Brown” data set. (Computational Analysis of Present‐Day American English by Kucera and Francis). After discarding 4% of the data judged to be spoken incorrectly, experimental recognition error rate was 2.3% (1.8% substitution and 0.5% rejection), with negligible difference in performance between male and female speakers. Experimental error rate for vocabulary subsets, ordered by frequency of usage, was 1.0% for the first 50 words, 0.8% for the first 120 words, and 1.2% error for the first 1500 words. An analysis of recognition errors and a discussion of ultimate performance limitations will be presented.
If we project the regression line (in the entropy versus logit(WER) plot from the Lee & Chen experiment) to a vocabulary of 26k words (entropy of 14.67 bits), we would predict a word error rate of 90.5% — which is a lot more than 2.3%.
Now, this projection is not at all reliable: isolated word recognition is easier than connected word recognition, especially when the words being connected include short monosyllabic function words that might be hypothesized to occur almost anywhere. But still, Chin's guess is that current ASR performance on the Doddington/Hydrick task would be quite poor — strikingly worse than human performance, and perhaps spectacularly so.
And he thinks that this striking human/machine divergence points to a basic flaw in the current standard approach to ASR. For his diagnosis of the problem, see his keynote address at Interspeech 2012.
I hope that before long, we'll be able to recreate something like to the Doddington/Hydrick dataset: a high-entropy recognition task on which human and machine performance can be directly compared. If this comparison works out the way Chin thinks it will, the plausibility of his diagnosis and his prescription for action will be increased.
Update — Although everyone seems to agree that research on less diffuse acoustic models (and their use in ASR) would be a Good Thing, issues with the LM weight (= "fudge factor") and the insertion penalty make this experiment a less-than-ideal way to compare machine and human performance on a high-entropy task. Following up on some of the comments below, I-Fan Chen has done a more extensive series of experiments, whose results he reports here.
So at some point, I think we will go ahead and record a couple of test sets for either (1) a random isolated word task, or (2) a randomly-generated complex nominal task. More on this later…
Joel said,
January 5, 2013 @ 7:20 pm
The problem may lie in using words as indivisible tokens in language models. For isolated word recognition, morpheme or syllable n-grams might present an important complement to the unigram frequency prior.
Vincent Vanhoucke said,
January 5, 2013 @ 7:20 pm
Indeed, ASR is overly reliant on the strength of the language model. Here is another way to see it. You state that we compute P(S|H)P(H). That's not quite true in practice: all systems typically compute P(S|H)P(H)^C, where C is a fudge factor which trades off the strength of the acoustic model against the strength of the language model. The shocking part is that a typical C = 12 to 16! We 'trust' the language model 12 to 16 times more than the acoustic model. I have seen big improvements in acoustic modeling lower this C by on the order of 2 points, but indeed we are still very far off.
[(myl) Indeed — in fact I've sometimes seen fudge factors as high as 30 or so. I originally had a paragraph and another equation about this, but decided to remove it so as not to delay getting to the point. Also, as I understand it, the fudge factor is partly there because the language model and acoustic model probabilities tend to be in different quantitative ranges, for less relevant reasons having to do with the way that they're estimated.]
Joel said,
January 5, 2013 @ 7:23 pm
Rather: high entropy words do not necessarily have high entropy sub-word structure.
[(myl) It's true that if a phonotactic model has (say) 2 bits of entropy per phonetic segment, and there are on average five segments per word, then you'd get an average per-word entropy of just 10 bits or maybe less. But on the other hand, for this kind of material, typical phone error rates for current HMM recognizers (with a phonotactic language model) are around 30% or a little worse, so the chances of getting all the segments in a word correct is only about 0.7^5 or about 17%.
You could do some things to improve the phone error rate — but then you'd be following Chin Lee's prescription. (Not that he's the only one making similar points…)]
Janne said,
January 5, 2013 @ 9:49 pm
Syllable-level models make a lot of intuitive sense. When you first start learning a new, completely different language, you have a problem even hearing the words correctly at first. But you soon "get used to" (build a model of) how the language sounds, and you can pick out words without having a clue as to their meaning or the sentence structure.
If I were playing with this, I'd probably try doing syllable-level and word-level recognition processes in parallel, and let the syllable-level recognition result dynamically skew the work-level language model.
Ciprian Chelba said,
January 5, 2013 @ 11:20 pm
Another experimental result pointing in the same direction is that even for tasks where the language models are really good (very large amounts of data, really good n-gram hit ratios at 3/4/5-gram orders respectively), the word error rates (WER) are still high. E.g. for voice search the WER is in the 17-15% range when using an n-gram LM built on 250 billion words, and whose 5/3-gram hit ratios on test data are 77%, and 97%, respectively.
re: P(S|H)P(H)^C
To be completely accurate, the log-probability used in ASR also penalizes the length of the word sequence H , and is computed as:
logP(S,H) = logP(S|H) + C * logP(H) – IP * length(H) – log(Z),
with Z a normalization constant independent of (S,H) that is ignored when comparing different H hypotheses for a given S.
That means that we are in fact using a log-linear model, with three main features: acoustic/language model log-probabilities, and word hypothesis length.
The weight on the language model score brings the differences between acoustic/language model scores for various H hypotheses (dynamic range of logP(S|H) and logP(H) scores) in the same range of values.
Andy Averill said,
January 5, 2013 @ 11:32 pm
Isn't there a demand for systems that perform very well given only a single syllable? I'm thinking of those phone menu systems that ask you to say your name or something else unpredictable (as opposed to just yes or no). In which case there's an incentive to bring down the error rate at that level, regardless of how superior multi-gram systems are.
[(myl) As far as I know, it's not now feasible to automatically recognize random surnames accurately — this is hard for humans as well, since the set of names used by residents in most modern countries has a long tail, and the variations in spelling are considerable as well. So any system that asks you to say a surname either has some basis for a very substantial a priori reduction in uncertainty (like the names of employees at a particular location, or the names in your personal contacts list, or some interaction with other information that you provide), or is just storing what you say for later use, perhaps by a human listener.
In general, people who design phone menu systems put a lot of effort into designing the interaction path so that the entropy at each choice point is as low as possible.]
Ethan said,
January 6, 2013 @ 12:14 am
@Andy Averill: Phone menu systems may exemplify a different task. I don't think it's true that your requested input is "unpredictable". Wouldn't they mostly be trying to confirm a bit of information that they already have, or select which of N entries in the menu is the best match to your response? In the case of your name, they probably already have a written version on file and task becomes one of deciding whether your response is a conceivable match. But I don't know how they would assign a numerical match score to "conceivable".
david said,
January 6, 2013 @ 9:32 am
I'm interested in the graph? Does logit(WER) vs entropy remain linear for other acoustic models? Does it retain the slope of 2/3? Is there a theoretical basis for 2/3?
[(myl) These are very good questions. I stumbled on the observed linear relationship in this case simply because I was curious about the nature of the relationship in the numbers that Chin sent me. I haven't seen such a relationship previously discussed, and I don't think that Chin has either; so the short answer is "I don't know, and it's not clear that anyone else does either…"
It would be relatively easy to do some tests to see what happens with other combinations of acoustic models, language models, test collections, etc. So stay tuned.]
bks said,
January 6, 2013 @ 10:37 am
If we couple speech-to-text to fMRI of thought-to-speech, we get thought-to-text. Now use speech-to-text coupled with inverted fMRI and, bingo-bango, Telepathy!
http://blog.pennlive.com/thrive/YOUNGFRANKENSTEIN.jpg
–bks
Dan Lufkin said,
January 6, 2013 @ 10:57 am
I'm trying to tie this information conceptually to my experience (~10 years' worth) with Dragon NaturallySpeaking. With first-level voice profile training on DNS version 12 I get a little better than 99% word-by-word recognition accuracy. DNS persistently asks for permission to come into your computer at night to scan your files of documents and e-mails to improve its acoustic model and apparently tracks every registered customer in this regard. (I don't participate because my files are in several languages and my profile ends up more confused.)
DNS works much better with long, smooth, coherent utterances than with choppy Word. By. Word. Dictation. My impression is that it samples an audio string two or three seconds long, which hints at a Markov chain of four or five links.
I appreciate that the details of DNS algorithms are highly proprietary but I wonder when I experience performance that appears to be a lot better than theory permits.
[(myl) I suspect that the effective perplexity of your dictation, relative to the language model that's been adapted to your previously-composed text, is somewhere between 100 and 300, and probably towards the lower end of that range. So you're not really experiencing something "better than theory permits" — current technology does pretty well with ~100-300 perplexity, but pretty badly with ~10,000-30,000 perplexity.
Programs like DNS also adapt their acoustic models to your voice and your typical recording conditions, which also improves performance significantly. I would be very surprised to learn that the internals of DNS are very different from the internals of other current state-of-the-art recognizers.
I also suspect that your word error rate (as calculated in the tests we're talking about) is somewhat higher than the 1% you cite — if it's really that good, then congratulations, you're lucky!
If you wanted to replicate something like the 1978 Doddington experiment, you could download one of the many big English word lists available on the internet (e.g. here), pick (say) 200 words at random from the list (for instance by getting line numbers from a random number generator operating over the total line count), read them one at a time into DNS, and see how well it does. (Or you could read them 10-20 at a time as if they were sentences — I'd predict that would be much worse…)
To get a number that's comparable to the current benchmark tests of continuous speech recognition, your could do the following experiment:
1. Pick a passage of text that's not exactly the sort of thing you usually dictate;
2. Transcribe it via DNS (with no edits) and send me the original and the dictated output;
3. I'll run NIST's software to determine the WER.
Or I could point you to the NIST scoring software and you could do it yourself.]
Rogier van Dalen said,
January 6, 2013 @ 11:52 am
I very much agree with Mark's call for measuring the error rates for human speech recognition on a similar task. It should be quite easy.
My hunch (which most people seem to disagree with, so I'm quite likely to be wrong) is that the error rates of human speech recognition on isolated words extracted from continuous speech is going to be at least 10, and it could well be 30. Two sources of errors I expect are (1) function words ("a" vs "the" vs "of") are often reduced beyond recognition; (2) morphemes ("danced the" vs "dance the") are often indistinguishable. I'm assuming there could be many other sources of errors. Any human unaware of the "phonemic restoration effect" is likely to overestimate how good they are at using acoustic information.
Whether I'm wrong or right, it seems obvious that to compare speech recognition by humans and computers, we need both numbers, not just one. (I was not at Interspeech so if a reason was given for not testing this, I've missed it.) (I'd also be delighted to be explained the significance of the performance "without" language model.)
Even without these numbers it is, I believe, uncontroversial that our acoustic models are not good. HMMs obviously don't model speech well. They also overestimate the dynamic range, as Vincent mentions, especially as the output distributions are over overlapping windows of features. But as far as I can see, the larger dynamic range is just a side-effect of using a bad model, much in the same way that N-gram language models generate over-short sentences.
[(myl) Human performance on words extracted from continuous speech is often quite bad, because the effects of coarticulation at the edges (to other words that are no longer there) are confusing, and also because of speaking-rate and other prosodic issues that are different from the expectation people have for words in isolation. There are sometimes good reasons to look at such things, e.g. see Ioanna Vasilescu et al., "Cross-lingual study of ASR errors: on the role of the context in human perception of near-homophones", InterSpeech 2011 – and that paper looks systematically at the effect of variable amounts on context on performance. (And a LLOG post helped recruit listeners for that study, I believe.) But it's not easy to draw crisp conclusions from such experiments about human speech perception abilities in the absence of language-model-like information.
In addition to the "random isolated word from the dictionary" method, you could also try "random complex nominals" generated by a process that would give at least a floor under the perplexity involved in recognition. Running such a process, I just generated "deadly polyethelene pawns", "retrospective calendar contractor", "unknowable credential amplification", etc. You could make it more realistic by varying the number of words in the generated sequences. Read versions of such sequences would tend to be hyperarticulated relative to less entropic material, but of course the machine and the human listeners would (or at least should) gain equally from that.]
p said,
January 6, 2013 @ 11:57 am
Currently, how do people evaluate HSR (Human SR)? It seems fine when we are dealing with isolated words. But when we have continuous speech, it will be very difficult to nullify the effect of language model that might be used internally by human brain. Has anybody come up with some creating experiments, yet?
One way to do that will be ask people to recognize continuous speech composed of nonsense-words. Or
words which have very low probability of following each other.
Mr Fnortner said,
January 6, 2013 @ 2:06 pm
To Janne's point: "When you first start learning a new, completely different language, you have a problem even hearing the words correctly at first. But you soon 'get used to' … how the language sounds", When I began studying Japanese, our instructor would conduct some tests entirely as dictation, speaking 10 or 20 sentences in Japanese for us to transcribe using kana and kanji. We were not asked to translate–indeed some vocabulary and sentence structures were completely unfamiliar to us–but to take what we heard and write it down the best we could. This proved to be invaluable as a way to (in my opinion) accelerate our ability to build a model of how the language sounded.
Bill said,
January 6, 2013 @ 4:00 pm
> If we project the regression line (in the entropy versus logit(WER) plot from the Lee & Chen experiment) to a vocabulary of 26k words (entropy of 14.67 bits), ….
While I like the line of argument, I'd be cautious about comparing perplexities between LMs of varying vocab sizes – in the current setup, the lm complexity varies in two dimensions (n-gram order and vocab size). It'd make a stronger case if the ASR system had a ~20K vocabulary and the human results were repeated with the same vocabulary.
[(myl) I agree that there are plenty of reasons not to trust that extrapolation. But i'm already surprised that the this little experiment produced such apparently lawful results, and I wonder whether a larger-scale experiment might produce a (more compex) model with some predictive value…]
Bill said,
January 6, 2013 @ 7:11 pm
It'd be interesting to see that larger-scale experiment. I think it might be difficult to find such straightforward relationships, since the role the LM varies so much depending on the task/domain. Fwiw, I've seen a rule of thumb : WER = k × sqrt(perplexity) `where k is a task dependent constant'
[(myl) That rule of thumb is also a decent fit for these four data points:
In this case, the model tells us that
WER = -0.008193976 + 0.010159849*sqrt(perplexity)
which predicts for a vocabulary of 26000 equally-likely isolation words
WER = -0.008193976 + 0.010159849*sqrt(26000) = 163%
The trouble, obviously, is that we're setting up the dependent variable in a linear model to be a number that's more or less bounded — for the WER to be greater than 100%, there would have to be quite a few insertions, which could easily be eliminated in a re-scoring step given that we know there's only one word per utterance. On the other hand, before sociolinguists learned about logistic regression, they got along OK using proportions as dependent variables in linear regression — and as long as you stay away from the bounds it can work pretty well… ]
D.O. said,
January 7, 2013 @ 12:55 am
Did that spectacular table in the OP include adjustment of the fudge factor? It seems to me that the larger is perplexity the more you have to rely on the acoustic model for your guess. Of course, if it were a straight Bayes that adjustment would happen automatically in the minimization procedure, but because it is not, it's hard to see what might be the theoretical grounds of keeping C constant…
[(myl) The "fudge factor" was set at 15 for the whole experiment, which gave optimal results for the 3-gram and 2-gram runs. It seems that for the 1-gram run, using a value of 14 will reduce the WER from 32.82% to 31.05%. Runs at even lower values are still underway. For the 0-gram case, the LM weight doesn't matter, obviously.]
Vincent Vanhoucke said,
January 7, 2013 @ 10:44 am
Here is an old paper that attempted to compare human vs acoustic model performance by removing both the LM and frontend effects:
http://people.xiph.org/~jm/papers/stubley99.pdf
Not necessarily relevant results nowadays, but interesting methodology that begs to be reproduced on a more modern setup. At the time I think I recall the conclusion being that a good ASR behaved very much like a non-native speaker in terms of noise robustness.
Dan Lufkin said,
January 7, 2013 @ 5:36 pm
I thought that a more realistic test for the sort of dictation I do would be to use a set of random coherent sentences rather than a list of random words. I took the first 100 Harvard Sentences from the IEEE transactions with the idea that a corpus of this sort would be a fair test of what actually amounts to an audio-to-text communication link.
The first 100 sentences had a total of 777 words. The dictation, made under realistic normal working conditions with a Sennheiser M3 microphone, resulted in 11 word mistakes for a score of 1.4%. Any of the mistakes could have been corrected within the dictation by a maximum of two keystrokes.
By the way, this response was dictated and there was one mistake: "two" for "to".
Andy Averill said,
January 7, 2013 @ 5:43 pm
@Dan Lufkin, heck, I type "two" for "to", or the like, nearly every day. Maybe my brain's ASR needs an upgrade.
Dan Lufkin said,
January 7, 2013 @ 7:09 pm
Andy — Yeah, that's another advantage of dictation: it may be the wrong word, but at least it's spelled right. Four of the mistakes on the Harvard Sentences were homonyms. DNS will get a lot of them right, but it missed on "the colt through his rider" and "so a button on."
Now I have those damned Harvard Sentences stuck in my mind. All of them make sense, of course, but they have a certain residual weirdness to them. I'm glad I didn't have to attend the committee meetings where they were worked out. "The two met while playing on the sand" and "Joe took father's shoe-box out" are particularly vivid to me. My next experiment is going to be to feed them to Mark V. Shaney.
Rogier van Dalen said,
January 8, 2013 @ 5:25 am
So when I said that measuring the error rates for human speech recognition should be quite easy, I was wrong. I do hope that someone comes up with a fair comparison on continuous speech (with half-elided function words and the like). The paper Mark cites seems to be a good start.
I don't understand how decoding with "no language model" or with a "0-gram" (?) works. Correct me if I'm wrong. Either the prior on sentences is uniform, or the language model is a unigram with a uniform prior per word.
In the former case, as Mark says, "the LM weight doesn't matter, obviously". The language model is a uniform distribution over an infinite number of sentences, which is a bit funny. I am not sure how one computes the perplexity on such a model and ends up with a number less than infinity.
In the latter case, the language model will prefer shorter sequences, which should result in longer words. E.g. "for an" will always be recognised as "foreign". But the language model will not just be a tie-breaker. Changing the fudge factor becomes equivalent to setting the "word insertion penalty". It then does matter and should be optimised. But I still don't understand what the resulting word error rate is meant to tell us, except that classification with a generative model with the wrong prior is silly.
It seems to me that the only reason to include the performance "without" language model is rhetorical. I'd still be happy to be proven wrong.
[(myl) My understanding is that the "0-gram" case indeed involved making all words equally likely. This is surely a coherent situation — one might have generated test data as strings of words selected with equal probability from a given set; and in this case, the per-word perplexity is surely the size of the vocabulary — at least for infinite strings generated by such a process.
But you're right, I think, that this doesn't address the question of when to stop. If the end-of-sentence symbol is considered as just another option that might be drawn from the urn, with a fixed probability on each trial — whether its probability is the same as all the real words or not — the distribution over sentence lengths will be quite unnatural, with a mode of 1 and exponential decay thereafter (see here for an informal argument, and here for a more formal one).
The "right" thing to do, I think, would be to impose an independent empirically-derived distribution over word counts; and in decoding, to modulate this distribution parametrically based on the observed utterance length. I suspect that this is not what Lee & Chen did; but I'll ask them and report back.
The thing is, this sort of semi-markov process ought to apply in the non-uniform case as well, as far as I can see: consider a sort of homomorphism of a bigram processl, where the choices are reduced to "word" and "END". This ought to generate the same unnatural-looking distribution of sentence lengths. So I'm not sure that the problem is special to the "0-gram" case.
Anyhow, this is one of the reasons why I think that a large-vocabulary isolated-word recognition task would be the best way to estimate current differences between human and machine "acoustic model" performance. And yes, the goal is a "rhetorical" one, in the sense that the task is not of much practical interest — it's just a way to focus attention on a particular aspect of the overall problem.]
Dan Lufkin said,
January 8, 2013 @ 1:04 pm
I earlier threatened to submit the first 100 Harvard Sentences to Mark V. Shaney and I now have the results. Mark returns 10 sentences, only the first of which is not precisely as in the original text: "Press the pants and sew a button on the road." This is probably derived from HS no. 23, "Press the pants and sew a button on the vest." It is interesting (possibly) that this is the only HS in which DNS made two mistakes. The "road" comes from HS no. 68: "This is a grand season for hikes on the road." As far as I can tell from a quick review, "on the" is the most common digraph, with seven instances.
The observation that MVS leaves this corpus nearly unaltered seems to me to indicate that it is essentially a zero-link Markov structure. I don't know yet how that translates into a perplexity score. Anyone?
Rogier van Dalen said,
January 9, 2013 @ 7:03 am
Mark, thanks for the clarification. The problem of word insertions and deletions (also caused in part by HMMs) is, I believe, usually counteracted with a word insertion penalty. At least, that is what I have always done. A unigram model with uniform weights ("0-gram") is special in that optimising the language model scaling factor is equivalent to optimising the word insertion penalty, which is a rather important detail. I therefore misunderstood your comment "the LM weight doesn't matter, obviously" as implying that a uniform prior over sentences is used.
Let me try to make clearer why would I not quote the performance for the "0-gram" case. I can't relate it to any process in humans, so to me it's meaningless in that sense. I also wouldn't put in in a graph. In the progression there is a step change: the unigram model with uniform weights is an untrained model (which I wouldn't call a "0-gram"), whereas the unigram, bigram and trigram models are trained. In the graph, the straight line from 1 to 0 corresponds to having less and less training data. Between 3 and 2 and between 2 and 1 it doesn't. I would argue that these line segments really traverse different dimensions. Even if they can be mapped to one, the entropy, I wouldn't trust that the behaviour of the WER is consistent. But I'd be happy to hear if I'm wrong.
I also wouldn't take the 69.2% number too literally, so I wouldn't put it in a table. With a system like that, all sorts of things may be taking place. One effect I suspect exists is that homophones are confused randomly (for a definition of "random" that depends on the implementation). E.g. a correctly recognised word /d uw/ could be "DO" vs "DU" vs or "DUE" (assuming I'm looking at the appropriate dictionary), and similarly for a number of often-occurring function words.
So the only reason I would quote the number is to say that it is obviously not a system one wants to look at. But maybe that's just me. I would stick with the graphs like in http://research.google.com/pubs/pub40491.html
A fair comparison between human and automatic speech recognition is important. Results for isolated-word recognition would be interesting. However, my worry is that ASR errors for isolated words would be representative of only a small part of the ASR errors in continuous speech.