Names in the Frequency Domain
« previous post | next post »
Yesterday evening at dinner, some members of the LSA Publications Committee were idly discussing the changes over time in fashions for given names. It's obvious that things change — but it's less obvious whether these changes are cyclic. It makes sense that out-of-fashion names might come back after a generation or two — but does this really happen on a regular basis?
So for this morning's Breakfast Experiment™, I fetched the data available here, which provides "National Data on the relative frequency of given names in the population of U.S. births where the individual has a Social Security Number (Tabulated based on Social Security records as of March 7, 2011)". The data comes in the form of 131 files, one for each year from 1880 to 2010, giving the count of SS card holders born in that year with each of a large number of first names (61,406 different female names and 36,742 different male names).
The lists include all names with counts of five or more in a given year — thus the file yob1980.txt starts like this:
Jennifer,F,58375
Amanda,F,35817
Jessica,F,33914
Melissa,F,31625
Sarah,F,25737
Heather,F,19965
Nicole,F,19910
Amy,F,19832
Elizabeth,F,19523
Michelle,F,19113
and ends like this:
Yvonne,M,5
Zackaria,M,5
Zackry,M,5
Zaire,M,5
Zalman,M,5
Zedric,M,5
Zell,M,5
Zenas,M,5
Zhivago,M,5
Zoe,M,5
(Yes, the dataset contains five males allegedly named Yvonne, and five others named Zoe, born in 1980.)
I turned this into two files with yearly counts per name — one for males and another for females — e.g.
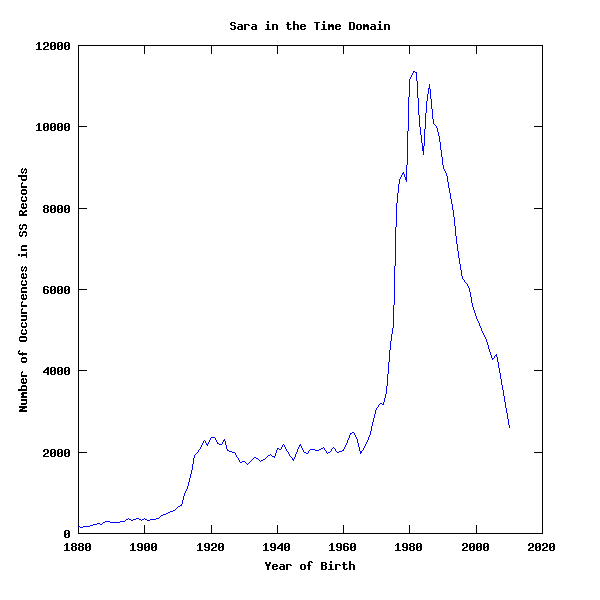
Sara 165 147 180 183 197 215 247 214 293 286 262 260 276 290 304 363 326 353 362 323 375 315 335 333 359 437 457 494 546 559 633 687 962 1121 1488 1913 1992 2147 2295 2172 2363 2349 2222 2183 2314 2034 2023 1995 1868 1750 1767 1708 1759 1861 1844 1774 1822 1902 1946 1870 2088 2071 2189 2021 1904 1803 2033 2178 2017 1968 2056 2074 2042 2077 2125 1970 2007 2109 1992 2028 2038 2200 2469 2486 2355 1975 2055 2214 2454 2795 3062 3201 3180 3480 4648 5130 8022 8706 8865 8646 11151 11349 11336 10080 9315 10548 11042 10083 10007 9707 8968 8842 8437 7893 7213 6683 6282 6151 6006 5618 5310 5146 4935 4756 4500 4269 4392 4008 3583 3030 2596
…which plots out as this:
The trouble with this approach is that the total number of people in the dataset by year is quite variable:
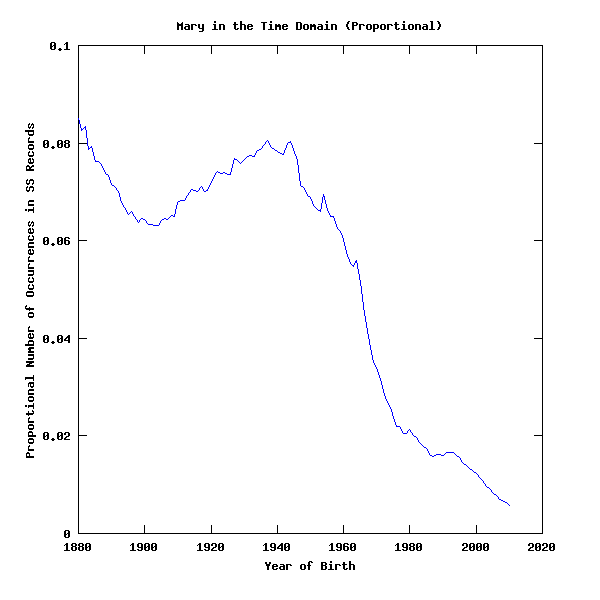
As a result, the counts in the time series looks very different if they're expressed as a proportion of the size of the pool of people represented in each year. Here's Mary:
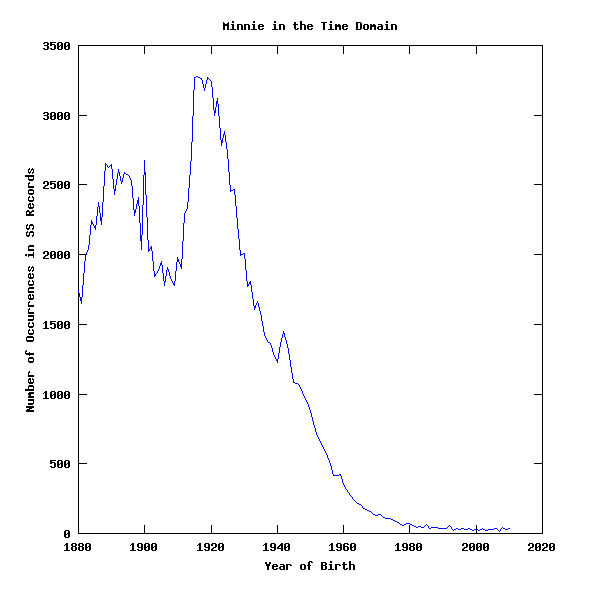
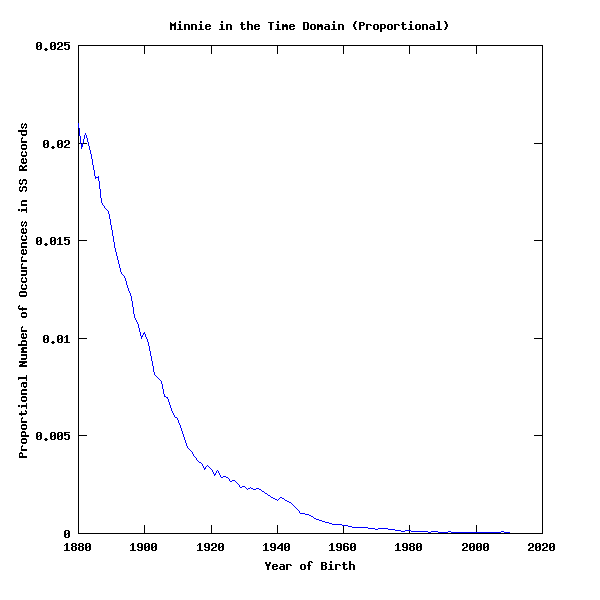
And here's Minnie:
asdf
(That's as far as I got over breakfast — finishing the write-up makes this a Lunch Experiment™ as well.)
Going forward, I'm using the proportional counts rather than the raw counts, and looking over a sample of the proportional time series plots, I don't see much evidence of cyclic recurrence. Basically, it seems that names come and names go, and sometimes names come and go — but it doesn't seem to happen very often that names come and go and come again, at least within the 131-year time period covered by this dataset.
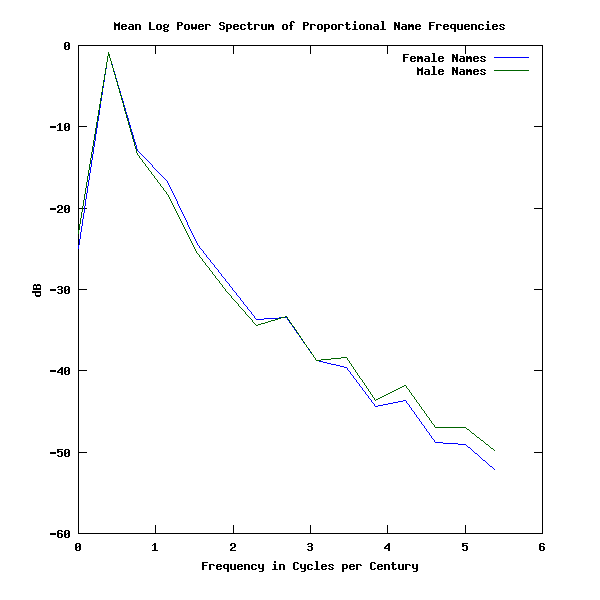
In order to look at this from another perspective, I calculated the log power spectrum for each of the 457 female names and 487 male names that were present in each of the 131 years in the database, and then averaged the results:
This seems to show that there's a substantial component at about 0.4 cycles per century, i.e. a period of about 250 years — which is roughly the lowest frequency that we could expect to see in this analysis — and approximately a 1/F decline after that.
A bit of poking around didn't turn up any other attempts to look at name-fashions in the frequency domain — maybe readers will point us to some.
I did find R. Alexander Bentley et al., "Regular rates of popular culture change reflect random copying", Evolution and Human Behavior 2007, which looks at turn-over rates in top-Y lists as a function of list size:
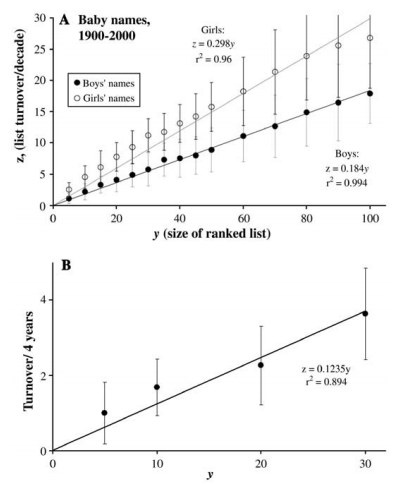
Turnover rate of Top y charts, plotted against y, the size of the list, for (A) boys’ names (filled circles) and girl’s names (open circles) and for (B) dog breeds. For baby names, the turnover rates are per decade and averaged over the 20th century. For dog breeds, the turnover rates were calculated based on 4-year intervals.
There's probably some way to relate this to frequency-domain parameters, but so far I don't see it.


Amy Reynaldo said,
May 5, 2012 @ 1:28 pm
You know, it would be a lot easier to use Laura Wattenberg's Baby Name Voyager. No need to wrangle the data and graphs yourself. Granted, you wouldn't gather your scientific proof, but it's a funky tool. (http://www.babynamewizard.com/voyager#)
[(myl) But it doesn't offer access to the underlying data, and thus no possibility to try looking in the frequency domain.]
Wattenberg's affiliated blog touches on naming trends and which sort of old names cycle back into style. Everyone seems to claim an ancestor named Isabelle when they name their baby Isabella, but where are the babies named Gertrude, Millicent, and Dorothy? For every toddler named Henry or George, we seem to be missing an Alfred or Herman.
[(myl) I don't see any evidence in the SS dataset that George is coming back:
]
Nick said,
May 5, 2012 @ 1:34 pm
This is very interesting – and I agree that the proportional plots are the most useful (I had initially assumed the lower counts would cause too much uncertainty in the graph, but it looks relatively stable – would be interesting to see with errors).
My intuition towards name-cycling would be that it would tend to be equivalent to about the average lifespan – people naming their children after relatively recently-deceased grandparents, but there should be a hint of this in the data set – perhaps naming children after living grandparents would actually exist as a cycle? I also would imagine that more cycling would happen with the less common names, as an elderly relative with an uncommon name might be a better candidate for naming from.
Wikipedia says that the US Census started in 1790, and the UK one approximately the same time. I wonder if this data is easily available somewhere? It would be interesting to see how that data behaves, and to compare the crossover period to see how they match.
Denis Moskowitz said,
May 5, 2012 @ 2:02 pm
Here's another plug for the Baby Name Wizard blog – take a look at http://www.babynamewizard.com/archives/2010/4/the-generational-sweet-spot-or-why-your-parents-have-such-bad-taste for some cyclical analysis.
[(myl) The "cyclical analysis" there is entirely hypothetical, as far as I can tell. It corresponds to the hypothesis that emerged in last night's dinner conversation. But there doesn't seem to be any empirical evidence that this hypothesis is actually true, unless I'm missing something.]
J.W. Brewer said,
May 5, 2012 @ 2:10 pm
The ssa.gov website can give you a run for years-of-birth from 1880 through 2010 of the popularity by year in rank-number terms (i.e., if the name was one of the 1000 most popular in a given year, it will give you a number from 1 to 1000) and that way you can definitely find via trial and error names whose popularity has markedly diminished and then returned. However, since being e.g. the 206th most popular name for girls does not equate to the same percentage of girls each year (and there's been a longterm trend where the total percentage of births covered by the most popular X names has been dropping), it's not a perfect match with the graphs myl in generating although one would think the trendlines would be at least loosely the same.
[(myl) The dataset I downloaded is the raw counts from which those the top-1000 lists were compiled.]
To give one specific instance: my younger daughter (born 2004) is named Lily, a name which per the SSA database bounced around from 1880 through 1930 within a range roughly between 250th most popular and 350th most popular. Then it went into secular decline, ultimately dropping out of the top 1000 altogether for a while in the '60's into the '70's. But then it came back, and started ascending rapidly, entering the top 200 (which had never happened in the 1880 et seq period) in 1998, then the top 100 in 2002, then the top 20 in 2009.
[(myl) Here's the proportional frequency plot for Lily in the U.S. Social Security dataset:
]
I don't know whether the trend was the same in the UK, but when the Who recorded "Pictures of Lily" in 1967, the name was out of the top 1000 in the US for newborns, but the titular Lily of the song is said to have been "dead since 1929" so perhaps a vaguely archaic-sounding name was desired. (Wikipedia's piece on the song notes that Lillie Langtry died in 1929, although Townsend has apparently said in a somewhat muddled interview that he'd had Lilian Baylis (1874-1937) in mind).
Mark Etherton said,
May 5, 2012 @ 2:26 pm
This website argues for significant changes in first names at the Industrial Revolution: http://www.galbithink.org/names/agnames.htm
Jean-Sébastien Girard said,
May 5, 2012 @ 2:45 pm
The cyclicness of French given-name trends is well-known and documented. The cycles are also far more obvious than in English, where the top names do not change all that much from year to year, but dramatic shifts happen all the time in French, and the top names have at times reached up to one in seven kids.
[(myl) Can you point to some documentation — and even better, to some data?]
LDavidH said,
May 5, 2012 @ 3:44 pm
It's interesting – I would have accepted the cyclical hypothesis, simply based on the number of babies and young children I know or hear about that seem to have names that sound old-fashioned to me. I guess we just trust our interpretation of our personal experience more than we maybe should!
[(myl) Exactly my reaction. I expected to see a lot of names that came roaring back after falling out of favor for 60 or 80 years, just as in Laura Wattenburg's hypothetical curves:
But I didn't find any names with such patterns (not that I checked all 90,000 of them), nor did the frequency-domain analysis show a peak in the 1 to 1.7 cycles-per-century range.]
diogenes said,
May 5, 2012 @ 4:42 pm
confessing to being perplexed. The Times (London) has regularly posted lists of the most common(frequent, in order to avoid pejorative overtones) baptismal names since at least 1950 and probably before. But in the UK.
David always used to top the lists for boy children
micah said,
May 5, 2012 @ 4:43 pm
I wonder if perceptions of cyclical naming have to do with general classes of names rather than specific names. For example, it's pretty easy to see on babynamevoyager that names beginning with vowels were more popular at the beginning and end of the 20th century than in the middle (and this is true of each vowel individually up to some small sample size weirdness with U, which makes me think it's a real trend). I could easily imagine that someone born in 1950 would grow up thinking that vowel-names sounded old-fashioned, and then transferring that impression to the newly popular vowel-names of the 80s and 90s, even though they formed the impression on Albert and Ethel and the new names were Ethan and Olivia…
diogenes said,
May 5, 2012 @ 4:51 pm
there is the Us site called babyname voyager…ok I just realised that you have gone through that …but I cannot see what any other data repository would give you that the list of baby names by month does not give you.
mgh said,
May 5, 2012 @ 5:11 pm
there is an entire chapter on this in Pinker's "The Stuff of Thought", covering whether names are cyclical, the trend for male names to become female names but not vice versa, and how new names arise.
D.O. said,
May 5, 2012 @ 5:34 pm
Perhaps, because people give now names in more diverse fashion (name entropy is rising, so to say), it might be reasonable to look at name-rank rather than to the number or proportion of counts. Or, if you do not want such crude measure, devide frequency of a selected name by frequency of, say, 10 most frequent names in the selected year.
[(myl) Your hypothesis that "name entropy is rising" seems to be false, in fact. At least if we restrict our attention to the ~500 names that occur in all 131 years, the entropy of the empirical distribution of female names in 1880 was 7.1, while the entropy of the distribution of female names in 2010 was 4.8. In the case of male names, the entropy of the distribution in 1880 was 6.5, while the entropy of the distribution in 2010 was 4.9. So it seems that "name entropy" is falling, not rising (though perhaps looking at the whole list for those years, or at every year in between, would tell a different story).
In any case, the dataset is available to all at the linked site, so the field is open for you to try any variations that you can think of.]
Steve Kass said,
May 5, 2012 @ 7:15 pm
Emily seems to have come (mostly before 1880), mostly gone, come back strongly, and started to fade. [chart]
Thanks for pointing out these files. I have no excuse now not to update Baby Unique, Not So Much.
[(myl) In a time-function of proportions on a linear scale, Emily doesn't really fit that description very well:
It's plausible that among the 90,000 names in the SS dataset, there must be some that fit the description — but it seems to be remarkably hard to find any convincing anecdotes, and much harder to construct a convincing case that such things are typical.]
D.O. said,
May 5, 2012 @ 8:10 pm
Female's name entropy for 1880: 5.26 for characteristic number of names 193; for 2010: 7.61 -> characteristic number of names 2026.
500 names seems to be too short for recent years. I might (no promiss!) do a Bedtime Experiment.
[(myl) You might be right — I'll look forward to seeing your results. But I just tried this on the whole list of female names from 1880 and 2010. And the entropy of the whole 1880 distribution is 7.6, while the entropy of the whole 2010 distribution is 5.6. This despite the fact that there are only 942 distinct names in the 1880 set (because of the relatively small sample of 90,993 women), compared to 19,698 distinct names in the 2010 set (for 1,759,010 women), so that the "absolute rate" (per-item entropy for equally likely choices) is 9.9 in 1880 compared to 14.3 in 2010, and the redundancy in 2010 is much greater, 14.3-5.6 = 8.7 bits per name, vs. 9.9-7.6 = 2.3 bits.]
Steve Kass said,
May 5, 2012 @ 8:26 pm
Granted, I suppose it was cheating to plot Emily logarithmically, but her name does seem to fit the bill in some ways. Is it possible that what you're looking for in a linear/proportional graph may be too restrictive?
Would Emily have been more "cyclical" if only she'd had less recent popularity? (Her up-and-down before 1970 would then be much more visible on your graph.)
It would be good (and interesting) to define "evidence of cyclic recurrence" mathematically, with a function that could be applied to a series of integers. The data do suggest that it's not the case that many or most names have "come and gone" more than once in popularity. But it would be good to have a well-defined cyclicality function.*
[(myl) Well, my look at the power spectrum was an attempt to operationalize that idea: if there is cyclic recurrence with a period of τ years, then there should be spectral power at a frequency of 1/(τ/100) cycles per century. If you look at (say) sunspot data this way, the periodicity pokes right out, just as anticipated.]
Would changes that were more more similar in range raise the value of this function? (Then a threshold might exclude many names that were ever in the top dozen or so, because their great fame would exclude other variations.) Would this function be higher if the ups and downs were especially large (Then a threshold might exclude names that were never – as opposed to ever – near the top)?
*Surely people who study time-series (loony stock price analysts aside) must know how to measure this, no?
Steve Kass » Baby Unique, Not So Much [updated again] said,
May 5, 2012 @ 8:42 pm
[…] Administration’s baby-name database, but it turns out there was more there than I realized. In his Breakfast Experiment™ of this morning, Language Log’s Mark Liberman mentioned this richer source of SSA name […]
rgove said,
May 5, 2012 @ 10:24 pm
What explains the substantial gap opening up around 1940 between the total number of male and female individuals represented in the data? The first thing that came to my mind was this passage from Freakonomics:
Assuming the data source has a minimum threshold of 5 per year, none of these girls will be included, unless they have enough namesakes in other states.
Steve Kass said,
May 5, 2012 @ 10:54 pm
Sure, though "periodic" (or sinusoidal, much like sunspots, which have a very regular period) is different than "has gone up and down and up again" (like "Emily" 's popularity). The power spectrum is by no means useless, though. It could debunk the silly Generational Sweet Spot idea that there's a 60-90 year cycle, at least.
It would also be interesting to see something other than the all-names average of the power spectrum calculations, too, even if all you're trying to identify is periodic trends. That average might spot a cycle length that occurs for a great many names, but it could entirely miss the fact (if it were true) that all names have cyclical popularity. I'm not sure what the right calculation is – maybe look at the top decile names' power at each frequency – but I'm analogizing: a hundred tuneful musical instruments producing individually periodic waveforms might have no one pitch that stands out when the spectra are averaged.
These specific comments aside, it seems like there must be some known statistical measure of "goes up and down and up and down" that might find Emily a bit different from many other names, and that would be robust to the amplitude of oscillations so long as they're big enough not to be noise, and robust to ups and downs that are separated by different distances, and so on.
Steve Kass said,
May 5, 2012 @ 11:24 pm
@rgove: I think a mistake might explain the gap you noticed. In the data I loaded, there is no striking gap. For example, for birth year 1960, I see 2,022,062 females and 2,132,588 males in the data. Neither of these look like what's on Mark's graph. (I get the same results as Mark for "Sara"s, so I think I've loaded the same data.)
Nevertheless, there is a small effect having to do with rare names. I calculated the percentage of people in the database whose names have counts for that year and gender of less than 20. Here's a graph. (The caption is slightly incorrect – it's between 5 and 19, not 5 and 20.)
This rare name effect may have some effect on the by-gender totals, but the totals are not correct in the graph above. Since 1975, the database has been stable at about 93% as many females as males.
(The possibility of mistakes in the SSN database can't be ruled out, either. It seems odd to me that that database contained twice as many women than men with birthyears 1897-1910.)
Yuval said,
May 6, 2012 @ 12:34 am
Haven't read through yet, but I'm pretty sure there's a typo – twice "different female names", where I'm guessing one should read "male".
[(myl) You're right — fixed now.]
Yuval said,
May 6, 2012 @ 12:46 am
Assuming that the total number of births per year should be steadily increasing, even at steeper slopes from year to year, how do you explain the erraticness of the total-name count over the years? A very unpredictable "long tail" of under-5-count names?
[(myl) This is the set of people who are in the the U.S. Social Security database as of March 7, 2011. That makes sense of the total-name count across time, if you think about it. More or less, anyhow.]
robert said,
May 6, 2012 @ 3:35 am
An obvious hypothesis to test is that name popularity is just a random walk, with no correlation from year to year. This doesn't fit the dramatic surges in popularity some names have, but could well account for most of the variability in names outside the top 100.
For a more sophisticated model, people pick names in basically two ways, either naming the child after someone, or picking a name at random, but within a certain frequency band.
When people name the child after someone, whether in the family or a celebrity they are effectively picking the name from the frequency distribution that held when that someone was named, x years ago, This is the naming mechanism people expect to produce cycles, but x is randomly distributed, roughly between 15-90. which apparently smears that signal out.
The rest of the time, people pick a name effectively at random from the frequency distribution among the population – the more common the name, the more likely they are to think of it – but they may deliberately exclude any name too common, and in some cases any name too rare. They might, for example, pick boys names in the rank range 20-10,000, weighted by frequency, though the actual cut-offs will be randomly distributed. This will contribute to the turn over in the top 10, because of people deliberately avoiding them, and it doesn't contain any cyclic component.
Baptiste Coulmont said,
May 6, 2012 @ 3:53 am
On the cycles of French names : You'll find informations in Besnard (&Desplanques) La Côte des prénoms (published from 1988 until today). Basically, when some first-names come back, their peeks are separated by more than one century (between 120 and 150 years). The cycle is a long one.
As for the US data, why don't you look at the ranks rather than the proportion : In France, a "popular" name in the 19th century was given to more than 10% of the babies. Nowadays, a popular first-name is a name given to .8% to 1% of all babies.
D.O. said,
May 6, 2012 @ 4:19 am
No luck. Still no repetition pattern even with new normalization. I won't bother everyone with details. But general question remains how you analize a timeseries if number of possible outcomes dramatically changes.
D.O. said,
May 6, 2012 @ 4:50 am
If we limit ourselves only to top-10 female names there are only 2 interesting comebacks — Elizabeth and Emma. Elizabeth was popular until mid-1920 and then in 80s and 90s. Emma was not very popular from 1890s to 2000s, but in top-10 before and after.
[(myl) The proportions time-function for Elizabeth doesn't look all that cyclic:
The plot for Emma looks a bit closer to a pattern of fade and recovery:
But the frequency-domain plot looks pretty 1/F; and in the context of the rest of the data, it seems more likely that this is a new fad for a name that, irrelevantly, was once somewhat popular, rather than a return to an earlier generation's status.
The time-functions are clearly indicative of "contagion" in baby naming, but it's not at all clear that there's any strong cyclic component even in individual time series.]
Terry Collmann said,
May 6, 2012 @ 5:06 am
Take a look at the statistics for John in the US – number one until 1923, still in the top five until 1972, still in the top 10 in 1991, and then a slightly erratic but increasing decline until 26th place in 2010. No sign of any cycle there. Mary shows an even more exaggerated fall from previous dominance: number one or two until 1965 and then a violent plunge, out of the top 10 by 1972, out of the top 30 by 1983, out of the top 50 by 2002 and 109th by 2010. Since a huge number of today's US babies must have grandmothers or great-grandmothers who were called Mary, I think evidence of the "grandmother effect" looks rocky on that name alone.
There's a site that will give you stats on baby names in England and Wales, but only from 1996: it shows clear evidence, myl, that George is coming back on the right side of the Atlantic, anyway, but similar trends for John and Mary to those seen in the US.
GeorgeW said,
May 6, 2012 @ 6:08 am
@Terry Collmann: "George is coming back on the right side of the Atlantic, anyway . . ."
George W. Bush may have deterred this name from half the U.S. population. Those of us reading the LL and bearing this name predate his presidency.
[(myl) Actually, the evidence for a "revival" seems to be just as strong in the U.S. as in the U.K. — and corresponds in time quite well with W's presidency.]
tk said,
May 6, 2012 @ 6:51 am
“…names might come back after a generation or two…”
How about a cultural/traditional dimension?
I am told that it is/was/ traditional in Ireland to name the first son after the paternal grandfather (the son’s father’s father: a patrilateral grand-patronym), the second son after the maternal grandfather (the son’s mother’s father: a matrilateral grand-patronym).
Here’s some anecdotal/personal data:
My great-great grandfather (the earliest of whom we have any data), born in the mid/late 18th C, was Denis. His son was Patrick [the immigrant, 1844], (birth order unknown, but birthday was Mar 16, 1812: St Pat’s is Mar 17. Coincidence?].
Patrick’s first son was Denis (grand-patronym; died young); second son was George (a matri grand-patronym); note: NMI.
Geo’s first son was Geo Albert (Albert a matrigrand-patronym). Second son John’s nymic origin unknown, no children.
Geo Albert’s son was Geo Matthew (Matthew a matri-grandpatronym).
Geo Matt’s first son was Geo NMI, a patri great-grandpatronym. Second son, Thomas W, a matri great grandpatronym.
Just sayin'.
I don't said,
May 6, 2012 @ 11:56 am
Mark,
Are you sure you haven't made a mistake in your chart "Total Name Counts Per Year"? Two commenters have mentioned oddities in what it shows, and I can't reproduce what you have from the SSA data. Here's what I get.
[(myl) I think that we did slightly different things. I restricted my time-series data to the set of names that occur in every one of the 131 years; the totals are then the totals by year in that set, not the totals by year in all the data. I don't think that this choice affects the qualitative conclusions, though to be serious about it I should check.]
J.W. Brewer said,
May 6, 2012 @ 12:58 pm
I take the point that when graphed out with the approach you've taken "Lily" and "Emily" don't look nearly as up-then-down-then-up-again as might have been supposed. I'm not sure I follow (perhaps due to statistical illiteracy) what's wrong with the "Emma" graph – or is it just that while it does empirically show a striking fade-and-recovery it doesn't suggest that this is a sunspot-like cycle we should expect to repeat indefinitely in the future on the same time scale? My last nominee for hypothesis-testing would be "Grace," which was 13th-most-popular in 1890 and returned to that spot in 2003, after falling as low as 397th-most-popular (in 1977) in between.
[(myl) I guess my tentative conclusion is two-fold: (1) If there's a genuinely cyclic component in U.S. given-name fashions, 130 years is not a long enough span of time to see the cycles clearly; (2) Examination of selected name-histories is not enough to tell us whether a name's deeper history has any systematic influence on its current fortunes — perhaps name-fashions rise and fall in a way that depends only on the current mix of names and popular-culture influences, without any significant effect of the name-distributions of now-dead generations.
FWIW, here's the plot for Grace:
]
One problem with any overly mechanistic cyclical theory is that in the U.S. naming practices observably vary with class/region/ethnicity/etc. and the proportions of the total childbearing population belonging to particular salilent naming-subcultures themselves have varied considerably over time. (Small example: "Kevin" when I was growing up was still a quite markedly Irish-ancestry name at least in my part of the country, but has apparently more recently been in vogue for Asian-American boys, at least in NYC, where babyname data is available broken down by race. But is the absolute number of Asian-American Kevins sufficient for this noticeable subgroup trend to move the needle on the overall national incidence of Kevins?) It's harder to get good data that's comparable over time on salient subnational groups (not that I'm complaining that the Social Security Administration isn't tracking babies by race/ethnicity/class/religion/etc.), but the national data itself is going to be a shifting aggregate of lots of such subgroups where patterns might perhaps be clearer on a standalone basis.
Steve Kass said,
May 6, 2012 @ 4:07 pm
Mark,
Thanks for clarifying. You might correct the description that precedes the "Total Name Counts Per Year" graph, which incorrectly says that it shows "the total number of people in the dataset."
Yout statistics might not change much if you included all names, but the restriction that the name must appear at least 5 times in every year seems like an odd one to enforce when looking for names whose number of appearances oscillates. Your requirement expressly eliminates names that oscillate with at least one very low (between 0 and 4) relative minimum.
In any case, it leaves out many unweird (but not typical grandparents') names whose popularity has arguably oscillated (by some unspecified criterion). To name a few: Achilles, Jacquelyn, Ken, Kathryn, Quentin, and Raquel.
KWillets said,
May 6, 2012 @ 6:33 pm
On the theory that naming follows mentions in books, I did some searches on various names on the Google n-gram viewer. There does seem to be some cycling and anticorrelation over periods of only a few years (eg Sara, Mary, Jane, Jenny). Mary had spikes around 1900 and 1930, which might have seeded the naming trends in the decades after, but so far I don't see any clear relationship.
J. Goard said,
May 6, 2012 @ 10:00 pm
@J. W. Brewer Re: Lily
That trend sure looks like it owes a lot to Harry Potter.
Matt McIrvin said,
May 6, 2012 @ 10:19 pm
I poked around with that Baby Name Voyager gadget a while back, and what I noticed was that it seemed as if names beginning with vowel sounds were quite popular for both boys and girls in the early 20th century, then almost vanished at midcentury, only to reemerge in recent years.
Names beginning with hard consonant sounds like K or P seemed to follow the opposite pattern, peaking sometime around 1960 and then gradually dropping after that. Softer, voiced consonants followed in-between or more complex patterns of fashion.
So that's my grand hypothesis. As I recall, it looked to be a cycle of somewhat more than 100 years, and the dataset wasn't large enough to encompass a full cycle.
Steve Kass said,
May 7, 2012 @ 1:46 am
Matt: Here's what the SSA data shows for names beginning with K or P, by gender and year.
Laura said,
May 7, 2012 @ 5:49 am
Another issue is that at least some Lilys (for instance) were actually named Elizabeth and nicknamed Lily, whereas since Lily Allen (and Harry Potter, and the Who) many more are simply named Lily. At least, that's my uninformed impression, quite possibly a recency illusion. If I wanted to call a child Lily, I might well name her Elizabeth officially (since it's a nice name and if she hated Lily she'd have the option of Liz, or Beth, or whatever) and just call her Lily. I doubt this affects the overall result much, if at all, though.
Alexander said,
May 7, 2012 @ 5:53 am
For me, the following site is easier to read than babynamewizard, and it has pretty much the same stuff
http://www.behindthename.com/
D.O. said,
May 7, 2012 @ 9:10 am
@Steve Kass & Matt McIrvin: If you are looking specifically for qusiperiodic patterns, look up names beginning with L and N for girls an J and U for boys. I am not sure whether there is anything deep about it.
The question that interests me now is how and why that happened that the number of female names in common usage is much larger than the number of male names. My estimate is twice as large over the years. This question surely has an answer.
John Emerson said,
May 7, 2012 @ 1:42 pm
Awhile back I did something on this. Not all of it holds up, but it still seems that names beginning with f , o, and e declined 1900-1960 while initial h was being replaced by k.
The top 10 girls' names seemed to change much faster than the top 10 boys' names.
http://www.idiocentrism.com/consonants.htm
John Emerson said,
May 7, 2012 @ 1:49 pm
Popularity of the name "Darwin": at peak 1910-1960 and then plummeted. Now coming back.I believe it's an indicator for progressivism or secularism. In my experience it's remarkably popular in rural areas.
http://www.thinkbabynames.com/meaning/1/Darwin
Matt McIrvin said,
May 7, 2012 @ 2:46 pm
D. O.: I think a common proposed mechanism is simple sexism. We think of masculinity as high-status, precious and fragile, so parents give their girls masculine-sounding names to increase their status, whereupon those names cease being regarded as masculine and people won't give them to boys any more. So men gradually ceded names like Ashley, Leslie and Stacy, etc., to women as they became infected with femininity.
However, I have nothing but anecdotal evidence for this.
Jamie said,
May 7, 2012 @ 4:10 pm
The cyclical hypothesis might be an example of confirmation bias – people note some examples of names that went out of fashion and came back, and then generalise this to all names.
J.W. Brewer said,
May 7, 2012 @ 4:22 pm
Matt McI – your theory (which I realize you are passing on rather than proposing from scratch) would explain why names seem to "tip" from predominantlly male to predominantly female more commonly than occurs in the opposite direction, but I think D.O. had a separate/broader question which is why innovation/diversity/rapid-turnover (of which adaptations of male/epicene names form only a small part) is more common for female names, at least in the modern U.S. One could presumably make up an equally plausible just-so story that parents are more willing to innovate with girls' names because they feel happy and self-confident about their daughters' futures and want them to be distinctive and individualistic whereas masculinity (alias "male privilege") is fragile and endangered such that parents of sons are thus incentivized to adopt the more risk-averse strategy of sticking more closely to a traditional inventory of "safe" names.
But more broadly, any theory of cyclicality of the sort that myl has been questioning/debunking above needs to deal with the fact that the speed of change (and thus of any actual cycling that could be teased out of the data) may systematically differ for boys' names and girls' names.
Barbara Phillips Long said,
May 7, 2012 @ 5:56 pm
While I've looked at Baby Name Voyager a lot, I haven't seen names reappearing in cycles in any obvious way. My (anecdotal) impression is that changes in styles of names allow some names to reappear in a way that looks like it is part of a cycle, but isn't a cycle for that particular name.
It seems more likely, as others have mentioned, that some names reappear because they fit a new trend. Other names become or stay skunked for various reasons. When I was naming my first child, the great-grandmother-to-be actively advised against reviving any of the names from her generation.
A forthcoming paper that's received a lot of play in the popular press apparently talks about the influence of hearing certain sounds on the popularity of names:
http://knowledgetoday.wharton.upenn.edu/2012/04/how-baby-names-can-help-marketers-predict-the-next-big-thing/
"According to Wharton marketing professors Jonah Berger and Eric Bradlow, that unintended impact of such natural disasters can tell marketers a lot about how the sights and sounds that we’re exposed to every day can impact our choices and, in turn, influence the consumer goods, music, movies and even baby names that become popular. Their paper, “From Karen to Katie: Using Baby Names to Understand Cultural Evolution,” is forthcoming in the journal Psychological Science."
Name junkies might also enjoy reading the blog of Nancy Friedman, who consults on product names and writes about words and names at:
http://nancyfriedman.typepad.com/away_with_words/
Her blogroll lists several sites that track or comment on names for people, plus many other language sites including Language Log.
John said,
May 7, 2012 @ 7:06 pm
Mark,
Can you share your converted data file (and technique for creating)?
Also, did you look at combined homophonic names (e.g., Sara, Sarah)?
[(myl) The original data files can be downloaded from the social security administration site — the national data is here:
http://www.ssa.gov/OACT/babynames/names.zip
And there's also state-specific data, which I haven't looked at:
http://www.ssa.gov/OACT/babynames/state/namesbystate.zip
Then I wrote some quick unix scripts and small octave programs — I'm not sure how much use they would be to anyone else, but I can try to clean them up and make them available if there's interest.]
John said,
May 7, 2012 @ 9:38 pm
Mark,
I did get the original files, and started to figure out how to convert them into the useful form you suggested, but kids in the house, Rangers on the tube, so I figured I'd ask you for your final product. :-)
However a little UNIX, R and BBEdit got me through it fairly painlessly.
Nana Batrychos said,
May 8, 2012 @ 7:21 am
When I was growing up in Australia in the 60s and 70s, it always seemed to me that the given names of my grandmother (born 1899 in Worcester, England) were equally old-fashioned and old-ladyish. Her name was Emily Ethel. So it struck me as interesting that Emily came back and Ethel didn't when I noticed Emily reappearing in the 80s and 90s.
There seems to me to be a distinct trend (possibly equally illusory or non-significant) for Asian-background Australians to choose (whether for themselves or their children) names that seem out of kilter with their generation. Almost all the Kevins and Joyces I know are either my parents' generation, or else young Asians, and the 30-40 year gap in ages is striking.
…Very anecdotal, but hard not to attach meaning to experience
Matt McIrvin said,
May 8, 2012 @ 11:12 am
When we named our daughter, the name we chose (Marjorie, my wife's grandmother's name) is actually a very old-fashioned name, in that it went out of style in the US several decades ago and is very uncommon for girls born today.
But, for some reason, it doesn't *sound* old-fashioned to my wife's ears or mine, like, say, Mabel or Gladys do (those are my grandmothers' names). I'm not sure why that is. It may be that Marjorie's time has come around or is about to, or maybe it's not really a cycle as such and there needs to be some stimulus.
Matt McIrvin said,
May 8, 2012 @ 11:15 am
…though my paternal grandmother actually went by her middle name; her given first name was Leila, which sounds both lovely and not old-fashioned at all, possibly because Leela is currently quite common among Indians.
blahedo said,
May 8, 2012 @ 11:47 am
A few have asked about why there would be a gender disparity in the earliest data. It's worth pointing out that this data is from the Social Security administration, which was only formed in the 1930s; I don't know that coverage was universal even then, and of course, anyone born before 1940 was not getting their SS card until later in life. (Even as late as the 1980s it was normal for kids not to get assigned SS numbers and cards at birth, though of course you needed them sometime before you started working.)
Anyway, my first guess on a gender effect there is that widows are disproportionately represented in the earlier part of the set, and that even allowing for childbirth-related death, women had a somewhat longer lifespan and thus a given age-cohort would have lost more of its men than its women. Birth years after 1940 will include most Americans born in those years and after 1990 very nearly all of them, but births before 1940 will have certain selection biases on them in this data set.
Ted said,
May 9, 2012 @ 11:26 am
I wonder to what extent the results would differ if you aggregated spelling and other name variants. Anecdotally, there seems to be a recent trend of giving kids names that sound like more-or-less traditional names but are spelled unusually (notable celebrity examples would include Dwyane Wade and Britney Spears).
This may not be easy to do scientifically because of the judgment calls required in deciding how to group names (e.g., does Jon go with John, Jonathan, or both? Are Nat, Nate, Nathan, and Nathaniel a single group? Which, if any, of those go with Jonathan?)
But it does seem that Sara and Sarah, for example, or Isobel/Isabel/Isabelle and perhaps Isabella, might show periodicity in the aggregate that the specific variants don't show individually, at least if the initial hypothesis that this sort of intra-name variation is increasing is correct.