Mark Liberman
To get an idea of what this might be good for, consider some things in the real world that can be successfully modeled as linear shift-invariant systems:
| Input | System | Output |
|---|---|---|
| laryngeal buzz | vocal tract resonances | vowel sound |
| noisy recording | noise-rejection filter | less noisy recording |
| signal | graphic equalizer | modified signal |
| signal | Dolby encoding | Dolby-encoded signal |
| Dolby-encoded signal | Dolby decoding | original signal |
| sound source | room acoustics | reverberant sound |
Most of the effort is simply definitional--you have to learn the meaning of technical terms such as ``linear,'' ``convolve,'' and so forth. We will also introduce some convenient mathematical notation. Beyond definitions and notation, only some easy high-school-level algebra is required; however, the resulting concept is a powerful one that will enable you to understand quite a bit about digital filtering and speech synthesis.
For mathematical convenience, we treat a digital signal s as an infinitely-long sequence of numbers. We can adapt the mathematical fiction of infinity to everyday finite reality by assuming that all signal values are zero outside of some finite-length sub-sequence. The positions in one of these infinitely-long sequences of numbers are indexed by integers, so that we take s(n) to mean ``the nth number in sequence s,'' usually called ``s of n'' for short. Sometimes we will alternatively use s(n) to refer to the entire sequence s, by thinking of n as a free variable.
We will let an index like n range over negative as well as positive integers, and also zero. Thus
![]()
We will refer to the individual numbers in a sequence s as elements or samples. The word sample comes from the fact that we usually think of these sequences as discretely-sampled versions of continuous functions, such as the result of sampling an acoustic waveform some finite number of times a second, but in fact nothing that is presented in this section depends on a sequence being anything other than an ordered set of numbers.
The unit impulse or unit sample sequence,
written ![]() , is a sequence
that is one at sample point zero, and zero
everywhere else:
, is a sequence
that is one at sample point zero, and zero
everywhere else:
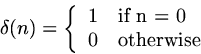
The Greek capital sigma, ![]() , pronounced sum,
is used as a notation for adding up a set of numbers,
typically by having some variable take on a specified set of
values. Thus
, pronounced sum,
is used as a notation for adding up a set of numbers,
typically by having some variable take on a specified set of
values. Thus
![]()
1 + 2 + 3 + 4 + 5
and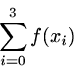
f(x0) + f(x1) + f(x2) + f(x3).
The ![]() notation is particularly helpful in dealing with
sums over sequences, in the sense of sequence used
in this section, as in the following
simple example.
The unit step sequence, written u(n),
is a sequence that is zero at all sample points less than
zero, and 1 at all sample points greater than or
equal to zero:
notation is particularly helpful in dealing with
sums over sequences, in the sense of sequence used
in this section, as in the following
simple example.
The unit step sequence, written u(n),
is a sequence that is zero at all sample points less than
zero, and 1 at all sample points greater than or
equal to zero:
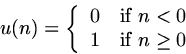
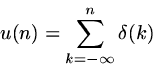
This is not a particularly impressive use of the ![]() notation, but it should help you to understand that it can
be perfectly sensible to talk about infinite sums.
Note that we can also express the relationship between u(n) and
notation, but it should help you to understand that it can
be perfectly sensible to talk about infinite sums.
Note that we can also express the relationship between u(n) and
![]() in the other direction:
in the other direction:
![]()
In general, it is useful to talk about applying the ordinary operations of arithmetic to sequences. Thus we can write the product of sequences x and y as xy, meaning the sequence made up of the products of the corresponding elements:
![]()
![]()
![]()
![]()
Any sequence can be expressed as a sum of scaled and shifted unit samples. Conceptually, this is trivial: we just make, for each sample of the original sequence, a new sequence whose sole non-zero member is that chosen sample, and we add up all these single-sample sequences to make up the original sequence. Each of these single-sample sequences (really, each sequence contains infinitely many samples, but only one of them is non-zero) can in turn be represented as a unit impulse (a sample of value 1 located at point ) scaled by the appropriate value and shifted to the appropriate place. In mathematical language, this is
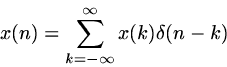 |
(1) |
This no doubt seems like a lot of trouble to go to, just to get back the same sequence that we originally started with, but in fact, we will very shortly be able to use equation 1 to perform a marvelous trick, so make sure that you understand it.
A system or transform T maps an input sequence x(n) onto an output sequence y(n):
| y(n) = T[x(n)] | (2) |
Systems or transforms come in a wide variety of types. One important class is known as linear systems. We already encountered the concept of linearity in discussing the propagation of sound waves: the linear propagation of sound in air means that the principle of superposition applies, so that the pressure disturbance resulting from two sounds propagating through the same region is just the sum of the pressure disturbances corresponding to the individual sounds. Linearity means the same thing as applied to sequences. We can express it mathematically like this:
| |
(3) |
Now we replace the expression x(n) in 2 with the re-expression of x(n) found in 1 to obtain:
![\begin{displaymath}
y(n) = T[\sum_{k= - \infty}^\infty x(k) \delta(n-k)]\end{displaymath}](signals/img18.gif) |
(4) |
That is, the sequence consisting of just sample k from x
can be rewritten as ![]() , our old friend the
unit impulse scaled to the value of x(k) and shifted to position
k. The response of system T to this sequence is just
, our old friend the
unit impulse scaled to the value of x(k) and shifted to position
k. The response of system T to this sequence is just
![]()
| |
(5) |
The original sequence x can be re-expressed as the sum of all of its individual sample values; by linearity, this lets us express T[x] as the sum over all samples of the response of T to a sequence consisting of only the given sample; this response is specified for a particular sample k by equation 5, and so make up the reponse to the original input, we just need to sum equation 5 over all k, which is:
![\begin{displaymath}
y(n) = \sum_{k= - \infty}^\infty x(k) T[\delta(n-k)]\end{displaymath}](signals/img22.gif) |
(6) |
However, there is one annoyance - we still must calculate ![]() for every shift k. This would be unnecessary if the response of T
to a shifted input was just an output shifted by the same amount. This
property, which is called shift invariance, holds of many
interesting systems. For example,
if we put a certain test signal into an acoustic resonator, and
then put the same test signal into the same resonator 20 seconds later,
we would expect the output to be the same, just shifted in time by
the same twenty seconds as the input (as long as the
resonator hasn't changed in the meantime).
for every shift k. This would be unnecessary if the response of T
to a shifted input was just an output shifted by the same amount. This
property, which is called shift invariance, holds of many
interesting systems. For example,
if we put a certain test signal into an acoustic resonator, and
then put the same test signal into the same resonator 20 seconds later,
we would expect the output to be the same, just shifted in time by
the same twenty seconds as the input (as long as the
resonator hasn't changed in the meantime).
In mathematical language, a system T is shift-invariant if and only if
| |
(7) |
| |
(8) |
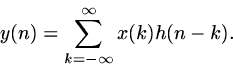 |
(9) |
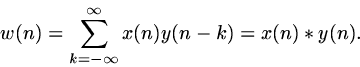
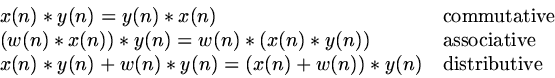 |
(10) |
This document was generated using the LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 signals.tex.
The translation was initiated by Mark Liberman on 10/11/1998