These are notes for a talk given in the IRCS Colloquium Series, Sept. 22, 2000. In effect, this is a sort of on-line handout.
Because this is a sketchy report of work in progress, please quote with care if at all.
Even in the absence of writing, human languages appear to develop and maintain vocabularies of roughly 10,000 morphemes, and at least 100,000 words or phrases whose meaning is not predictable from their constituent parts. This presents a formidable task for the individual language learner, who must learn words from a small number of uses in context, and must manage to remember such a large inventory of arbitrary pronunciations.
On a different scale of space and time, this also presents an extraordinary challenge for the speech community, which must must somehow form and maintain a consensus about these tens of thousands of complex and arbitrary conventions. This is accomplished despite the fact that the conventional knowledge at stake is tacit: the individuals involved typically don't know what they know about word pronunciation, and don't try to discuss the details of this knowledge.
Given how hard it is to get groups of people to agree about almost anything, it's natural to look for a method that doesn't depend on negotiation. Perhaps there was some initial naming authority, as in Genesis 2:19-20:
And out of the ground the Lord God formed every beast of the field, and every fowl of the air; and brought them unto Adam to see what he would call them: and whatsoever Adam called every living creature, that was the name thereof. And Adam gave names to the cattle, and to the fowl of the air, and to every beast of thefield...
Or perhaps there is a natural or original language, including a vocabulary, that the first humans spoke, and that we would naturally speak ourselves if we had not been taught otherwise. This is the implication of the experiment that Herodotus reports:
Now the Egyptians, before the reign of their king Psammetichus, believed themselves to be the most ancient of mankind. Since Psammetichus, however, made an attempt to discover who were actually the primitive race, they have been of opinion that while they surpass all other nations, the Phrygians surpass them in antiquity. This king, finding it impossible to make out by dint of inquiry what men were the most ancient, contrived the following method of discovery:- He took two children of the common sort, and gave them over to a herdsman to bring up at his folds, strictly charging him to let no one utter a word in their presence, but to keep them in a sequestered cottage, and from time to time introduce goats to their apartment, see that they got their fill of milk, and in all other respects look after them. His object herein was to know, after the indistinct babblings of infancy were over, what word they would first articulate. It happened as he had anticipated. The herdsman obeyed his orders for two years, and at the end of that time, on his one day opening the door of their room and going in, the children both ran up to him with outstretched arms, and distinctly said "Becos." When this first happened the herdsman took no notice; but afterwards when he observed, on coming often to see after them, that the word was constantly in their mouths, he informed his lord, and by his command brought the children into his presence. Psammetichus then himself heard them say the word, upon which he proceeded to make inquiry what people there was who called anything "becos," and hereupon he learnt that "becos" was the Phrygian name for bread. In consideration of this circumstance the Egyptians yielded their claims, and admitted the greater antiquity of the Phrygians.
Or perhaps words developed somehow by extension of an inventory of natural cries, as Rousseau thought [quotes from Essay on the Origins of Language):
The passions have their gestures, but they also have their accents; and these accents, which thrill us, these tones of voice that cannot fail to be heard, penetrate to the very depths of the heart, carrying there the emotions they wring from us, forcing us in spite of ourselves to feel what we hear. [...]
It is neither hunger nor thirst but love, hatred, pity, anger, which drew from [people] the first words. Fruit does not disappear from our hands. One can take nourishment without speaking. One stalks in silence the prey on which one would feast. But for moving a young heart, or repelling an unjust aggressor, nature dictates accents, cries, lamentations. There we have the invention of the most ancient words. [...]
To the degree that needs multiply, that affairs become complicated, that light is shed, language changes its character. It becomes more regular and less passionate. It substitutes ideas for feelings. It no longer speaks to the heart but to reason. Similarly, accent diminishes, articulation increases. Language becomes more exact and clearer, but more prolix, duller and colder.
This was later labelled the "ouch" theory of language origins. Other theories look to a basis in imitative sounds or vocal miming -- the equally infamous "ding dong" and "yo heave ho" theories -- with again a gradual (and mysterious) progression towards a full vocabulary of arbitrary vocal signs.
Of course, today we find it implausible to imagine a population of biologically modern humans without a language. We presume that spoken language co-evolved with the hominid line, and vocabularies likewise. Still, the creation and maintenance of a social consensus about words and their pronunciations looks like a hard thing to do.
It's not easy to get an empirical grip on the problem of vocabulary creation. We can look at how new words emerge in cultures with a fully developed language; we can look at large-scale borrowing in contact situations; we can look at cases in which a language can be argued to have emerged out of relatively primitive raw materials, as in the underground sign language observed in Dutch oralist schools in the 1960s, or the recent emergence of Nicaraguan sign language. In none of these cases do we have much information about the dynamics of the process of invention and convergence.
Despite the lack of quantitive evidence, there are some suggestions that a full linguistic system can emerge quickly, perhaps within a generation, including a normal sort of vocabulary. This has led D. Bickerton to suggest a sort of cross between the Psammetichus experiment and the television show "Survivor", whose details are probably better left to the imagination. Such experiments are not likely to be carried out, and of course their interpretation would be difficult in any case.
These are also sometimes called "individual-based models." Under any name, they are models in which ensembles of parameterized entities ("agents") interact in algorithmically-defined ways. Individual interactions depend (often stochastically) on the current parameters of the agents involved; these parameters are in turn modified (again often stochastically) by the outcome of the interaction. The universe in which the agents interact may be more or less structured, and the patterns of interaction may be more or less complex.
When applied to language, a model of this kind is most naturally construed as a representation of cultural evolution, but it is not hard to generalize such models in a biological direction, e.g. by setting a subset of the parameters (the "genotypic" ones), and then evaluating "fitness" over some rounds of "learning" and/or "communication" in the artificial universe, with survival and/or reproduction of entities affected so as to modify the expected distribution of genotypic parameters in the next round.
For agent-based modeling in general, the key idea is:
In other words, we can treat patterns of social behavior just like examples of organic form.
One way to use agent-based modeling is to demonstrate by example that such-and-such a system can emerge as a consequence of the interactions of agents whose programs do not appear to include the emergent property in any obvious way. This is usually of limited interest, because it is really just a particular kind of programming exercise. If a problem can be solved by any algorithm at all, it can certainly in principle be solved in the agent-based-modeling style. We just need to be clever enough in designing the agents' programs and the world that they interact in. Unless the demonstrated method is of practical value, or the problem has resisted solution by less indirect means, this is merely an empty display of virtuosity in coding. Such a display can be helpful in persuading uninformed people to be impressed by the emergent properties of complex systems, but it doesn't in itself improve our understanding of the system being modeled.
More enlightening results can be achieved, however. We can show that certain properties naturally emerge from broad classes of very simple agent interactions -- but not from others. We can show that certain kinds of agent programs will tend to "win" in competition with others, across a broad class of modes of interaction, and that this can plausibly lead to the evolution of certain kinds of social systems. Finally, we can show that the observed behavioral propensities of individual creatures naturally interact to produce structures of the kind that are observed in their social practice. Results of these kinds make it possible to believe that agent-based modeling has an appropriate place in scientific reasoning, and that in principle it can help us to understand the (genetic and cultural) evolution of language.
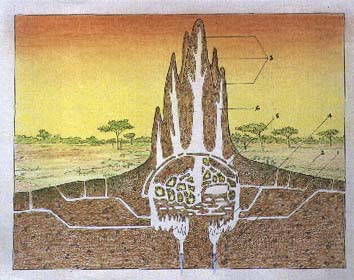
Termite mound algorithms:

E. Bonabeau et al., Self-Organization in Social Insects, 1997:
Self-organization was originally introduced in the context of physics and chemistry to describe how microscopic processes give rise to macroscopic structures in out-of-equilibrium systems. Recent research that extends this concept to ethology, suggests that it provides a concise description of a wide rage of collective phenomena in animals, especially in social insects. This description does not rely on individual complexity to account for complex spatiotemporal features which emerge at the colony level, but rather assumes that interactions among simple individuals can produce highly structured collective behaviors.
The results on termite modeling are moderately encouraging. The basic observational foundation is Bruinsma's (1979) PhD dissertation. Working with Macrotermes subhyalinus termites from Kenya, arranged in groups near a queen, he observed simple behavioral dispositions that lead to the construction of pillars and roofed lamellae around the queen. He identified several positive feedback mechanisms, involving responses to a short-lived pheromone in the deposited soil pellets, a long-lived pheronome along travel paths, and a general tendency to orient pellet deposition to spatial heterogeneities.
Deneubourg (1977) introduced a simple model with parameters for the random walk of the termites and the diffusion and attractivity of the pellet pheronome, which can produce a regular array of pillars. Bonabeau et al. (1997) extend this model to include air convection, pheromone trails along walkways, and pheromones emitted by the queen; in this extended model, "under certain conditions, pillars are transformed into walls or galleries or chambers", with the different outcomes depending not on changes in behavioral dispositions but on environmental changes caused by previous building. Thus "nest complexity can result from the unfolding of a morphogenetic process that progressively generates a diversity of history-dependent structures."
More satisfactory models exist for simpler social-insect behavior, for example the collective "decision making" of ants in chosing a path. "Ants deposit a certain amount of pheromone while walking, and each ant probabilistically prefers to follow a direction rich in pheromone rather than a poorer one." These simple rules are enough to allow ants to choose the shortest path around an obstacle. As shown in the illustration below, a group of ants will also choose one of two equally good paths (by symmetry breaking) without any leadership or explicit collective decision-making. The idea of applying such techniques to more complex problems has engendered a new mini-field known as "Ant Colony Optimization",
Evolution of reciprocal altruism
(Game-theoretic approaches to the evolution of cooperation, developed in the 1980's. Axelrod on the Iterated Prisoner's Dilemma game.)
(Probably the most successful and widely known application of agent-based models).
Lindblom et al. on the emergence of phoneme inventories. (Lindblom, B., MacNeilage, P., & Studdert-Kennedy, M. (1984). "Self-organizing processes and the explanation of phonological universals". In Butterworth, B, Comrie, B. & Dahl, O. (eds.) Explanations for Language Universals. New York: Mouton: 181-203.)
VUB language origins group
-- their publications
page
Bart de Boer
Luc Steels
Edinburgh Language Evolution and Computation
group-- their publications
page
Jim Hurford
Simon Kirby
Princeton
Institute for Advanced Study Theoretical Biology Group
We will try to find simple programs for interacting agents that lead to successful emergence of patterns of word pronunciation. As in the case of "ant colony optimization", we'll look for algorithms that can accomplish this without requiring any designation of authorities or any explicit negotiation to reach consensus. More important, we'll look for equally simple programs that fail, and we'll try to generalize about the differences.
What is the definition of success and failure? At the most basic level, success is social convergence combined with lexical differentiation. The goal is: "people are (mostly) all the same, but words are (mostly) all different." Or to put it another way, everyone winds up with pretty much the same ideas about how words are pronounced, and these pronunciations do not include an excessive number of homophones. This is the fundamental requirement for successful communication within a speech community.
We will look for classes of models that are robustly "successful", in that their success does not depend on finicky tuning of parameters or lucky choices of random seeds; and we will try to characterize the properties that such classes of models share. We'll also look for model properties that lead robustly to "failure".
The emergent structure that we are looking for is almost pathetically simple. Nevertheless, there are interesting generalizations about the types of agent-programs that succeed or fail in creating it.
As a preview of where we are going, we can say that two key ideas are enough to ensure success:
These are plausible ideas about human language. We know that human word pronunciations are variable, and that the effect of (even short-term) experience is usually to shift the distribution of outputs in the direction of the distribution of inputs. We also know that many aspects of phonetic perception are categorical, for instance in the sense that discrimination across category boundaries is much better than within them.
Note that we are not yet looking for an evolutionary model. The current goal is to just to find a class of simple algorithms, which can run in each member of a speech community to produce social convergence along with lexical differentiation. Once this problem is solved, we can ask how the propensity to act this way might have evolved.
So here is one extremely simple model that works. The exposition will be informal, and the demonstrations of asymptotic behavior will be anecdotal.
| Word pronunciation target: | Binary vector (sequence of vectors of binary "distinctive features") |
| Belief about word pronunciation: | Probability distribution over possible pronunciation targets; each feature is a binary random variable. |
| Word pronunciation instance: | Random binary vector (one value from each feature). |
| Initial conditions: | Random assignment of 1 or 0 to each feature for each person. |
| Channel effects: | Additive noise, features do not interact in transmission. |
| Perception: | Assign input feature-wise to nearest binary vector (= "categorical perception"). |
| Conversational geometry: | Circle of pairwise relations of errorless deictic naming among N people. |
| Update method: | Linear combination of previous belief and current observation ("leaky integration"). |
| Update timing: | After every conversation. |
Put slightly more formally, each word pronunciation is a bit vector S, so that a pronunciation occurring at time t1 might be:
St1 = [0 1 1 0 1 1 1 0 1 1 0 0 1 1 1 0 0 0 1]
We can think of these as being the concatenated values of the distinctive feature vectors for the phonemes in that particular word. Real phonological (and phonetic) systems are more complicated, but not in ways that affect the basic argument here.
An individual's belief about the pronunciation of a particular word, however, is represented as a vector of probabilities P, one for each of the bits of the pronunciation vector S.
Pt1 = [.058 .353 .813 .01 .139 .203 .199 .604 .272 .199 .015 .747 .445 .932 .466 .419 .846 .525 .203]
On each occasion of pronouncing a word, the speaker chooses 1 for each bit Fi with probability Pi, and 0 with probability (1-Pi). In other words, belief about word pronunciation is a random variable whose values are binary vectors.
Some random noise ν will then be added in the transmission channel, and the hearer will receive a noisy version of the speaker's production. The hearer then maps the input back into the boolean space, by mapping each value onto whichever of {0,1} is closest, so that the hearer's version H is T(S + ν), where T is a thresholding function of the form
Ti(x) = 1 for x >= .5
0 for x < .5
In other words, perception is "categorical".
The hearer then update his belief about the pronunciation of that word, replacing the old belief vector P with a linear combination of P and H:
Pnew = αPold + (1-α)H
for some update constant α.
To give an anthropomorphic interpretation to a grossly oversimplified example, we can imagine a system with exactly two binary features. Perhaps the first one as a choice between /d/ and /g/, and the second as a choice between /a/ and /i/. Then the space of possible pronunciations can be expressed as the four strings /da/, /di/, /ga/, /gi/. An individual's belief about the pronunciation of a particular word is represented as a vector of two probabilities, each governing the choice of one of the features. On each occasion of pronunciation of a particular word, a speaker choses one of the four possibilities [0,0] [0,1] [1,0] [1,1], according to the probability distribution determined by his belief about that word. Some random noise is added, so that e.g. [0,1] might become [-.13, .65]. The hearer then maps this back to the nearest binary vector, in this case the same as the transmitted vector [0,1], and updates his own belief about the pronunciation of that word by taking a weighted average of his old belief and his current perception.
Of course, all of the model characteristics sketched above can be changed. We'll discuss below the consequences of changes to many of them.
This simple model "succeeds" -- though some equally simple models will "fail." It converges, after a while, on a set of set of word-pronunciation beliefs that are shared across the population, but tend to be different for different words.
In the plot below, we show "time" -- denominated in iterations around the conversational circle -- along the x-axis, and "belief" -- the probability value associated with the random variable for a particular feature -- on the y-axis. The plot shows the evolution of one feature for two individuals (in this case those in the 1st and 4th positions in a circle of 10) who happen to have been initialized with opposite values for this feature. The pictures will be qualitatively similar for other individuals and other features.
(N.B. in the simulations below, the noise term is divided into an "output error" and an "input error". In some kinds of models, not discussed here, this distinction matters. For current purposes, the two sources of noise can simply be added. In the simulations below, added noise was taken from a uniform distribution, from -x to +x for the cited value x).
|
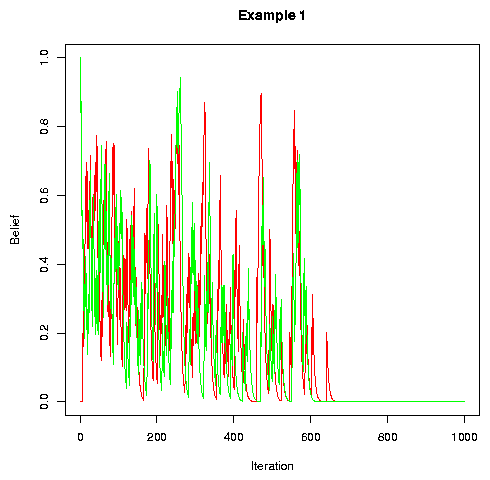 |
If we look at lots of examples, we find that values appear always to converge across individuals, and each Pi always converges to 1 or 0, the exact values of course depending on how we seed the RNG.
It's gratifying that such a simple model produces the right sort of result. Maybe the problem is not so difficult! Does every generally similar model behave similarly? Let's look at the results of changing some of the modeling assumptions.
It's not very realistic to assume that the outputs are binary vectors: we know that pronunciation is highly variable in gradient as well as categorical ways, and not only across speakers but among the productions of a single speaker. Luckily, it turns out not to matter whether the outputs of the system are quantized at all.
What does nonquantized output mean? In any case, the internal representation for a word's pronunciation is a vector of real numbers between 0 and 1. In the case of categorical output, we choose 0 or 1 for each vector element, choosing 1 for Si with a probability equal to the number stored in Pi. We then add noise and send the transmission on its way to the hearer. In the case of nonquantized output, we might for instance forget about making any binary choices, and simply send the underlying vector of real numbers, again with added noise. Here we are equivocating on the meaning of the values Pi: they were probabilities in a random variable, and now they are gradient signal values values to be transmitted. The equivocation is harmless because the two interpretations apply in different models.
Now the actual transmission does not send symbols, but rather signals in a continuous phonetic space. In terms of our earlier simple example, we can imagine an (articulatory or acousti)c continuum between /d/ and /g/, and another between /a/ and /i/. When we were treating output as quantized or categorical, the speaker picks a random "target pronunciation", say /da/. This gives an output target (in the phonetic space) for a canonical /d/ and another for a canonical /a/. The speaker's speech production apparatus now adds noise to these targets and sends out the resulting signal.
Now that we are treating output as unquantized, the speaker does not bother to choose between /d/ and /g/ or between /a/ and /i/, but simply picks a point on the corresponding phonetic continuum that encodes the real number stored for the feature in question. If the /d/-vs.-/g/ feature has the value 0.7, then (s)he chooses a point 0.7 of the way along the /d/-vs.-/g/ continuum and transmits it.
If we are treating input as unquantized (non-categorical), then the hearer would not bother to quantize the input into one of the (here four) possible symbol sequences, but would just uses the real number sequence directly in updating his or her beliefs.
In actual modeling runs, we would normally assume a more reasonable number of features per word (say 20 or so), but this choice of scale does not have any effect on the issues under discussion in this section.
Anyhow, in Example 1 above, both output and input were treated categorically. If we treat output as gradient, convergence is generally faster. Intuitively, this is because more information is being provided about the speaker's internal state, and so the listener's adaptation will be be more efficient.
|
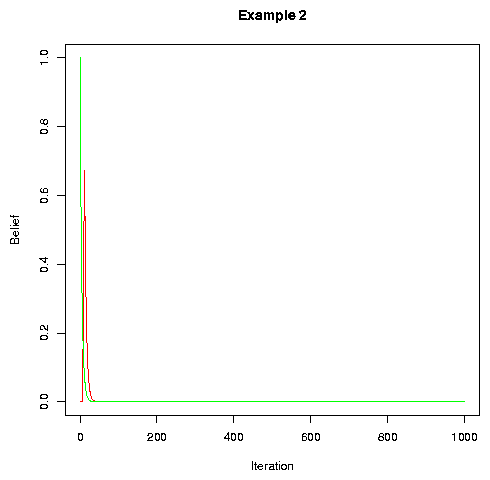 |
Of course, this model is even more unrealistic than the first one, in the sense that human speaker's phonetic outputs are surely not arbitrary values in a multidimensional phonetic space, but rather are clustered around discrete targets determined by the phonological system, with some provision for transformation of the space by individual and contextual variation. However, it is nice to see that the model's convergence is not at all sensitive to the assumptions that we make about quantization in the output: it will continue to work even if the there is no quantization at all, and would presumably work with some sort of complicated semi-quantization that would better reflect the real situation.
Nevertheless, it is not the case that quantization never matters. With gradient input and categorical output, for example, the process doesn't converge at all! Instead, beliefs wander around the available space indefinitely, in a random walk. The same is true if both output and input are gradient.
This is the first and perhaps most important generalization about such models: "categorical perception" seems to be required for robust convergence, but categoricality on the production side is not required or even necessarily preferred.
Here is the case of categorical output and gradient input:
|
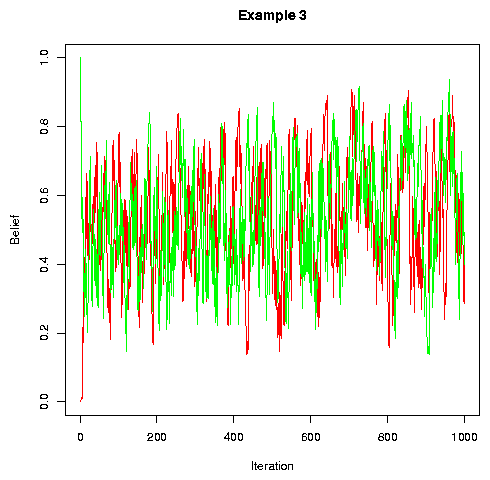 |
With non-categorical perception, beliefs wander not only in "time" (across iterations) but in "space" (across individuals at a given point in the sequence of iterations). Thus the range of beliefs found in the population about the pronunciation of a given feature in a given word at a given "time" grows with population size. As a result, the expected efficiency of information transmission between randomly selected individuals goes towards zero. (Note that the x- and y-axis labels are mistakenly reversed on the two plots below)
| Population range of beliefs in a circle of 20 people | Population range of beliefs in a circle of 40 people |
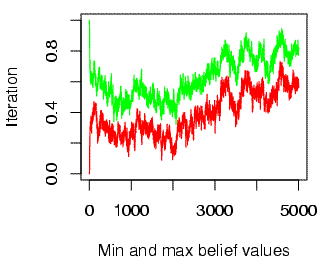 |
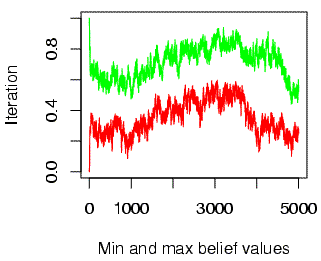 |
With a larger constant on the "leaky integrator of belief", convergence is slower (compare to example 2, which is the same as example 4 except for 0.8 instead of 0.9 update constant):
|
 |
|
 |
Permuting "people" randomly between every turn causes faster convergence (because values are spread more efficiently):
|
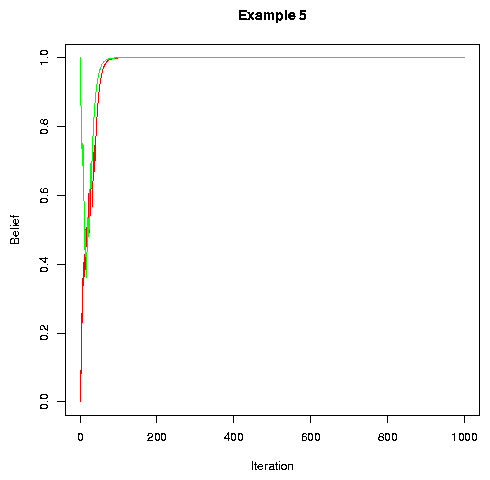 |
In general, adding more noise (up to a point) and randomly permuting the speakers tends to speed convergence. Example 6 is the same as example 1 but with more noise and with random permutation of speakers between turns.
|
 |
|
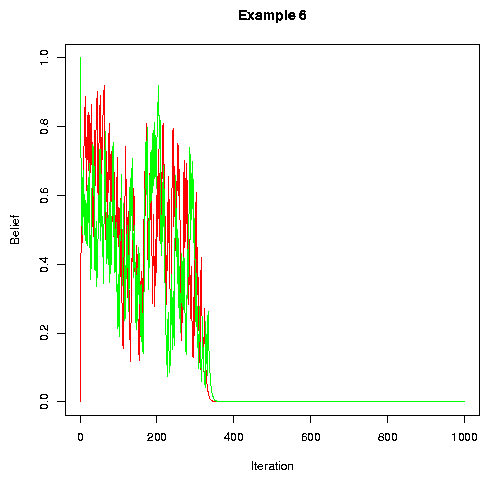 |
If we update after every cycle of conversations, rather than after every conversation, convergence tends to take a little longer, but still happens:
|
 |
|
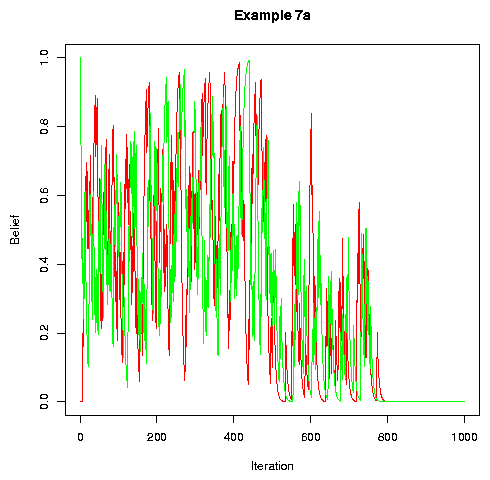 |
|
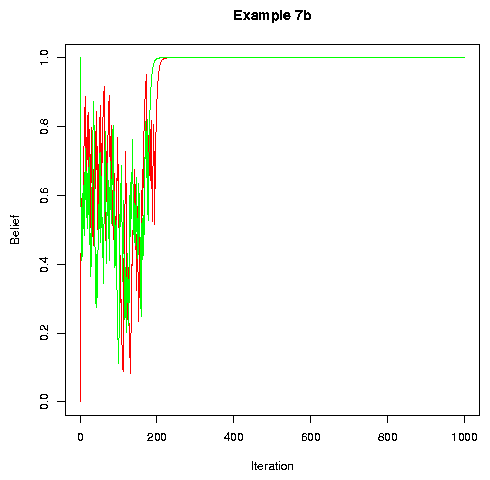 |
With no noise and no permutation, we can get a limit cycle. This is a sort of degenerate case for models of this type. Crudely, if the social interaction is too symmetrical, then we can't get the required symmetry breaking. Obviously no real-world situations will ever have this problem.
|
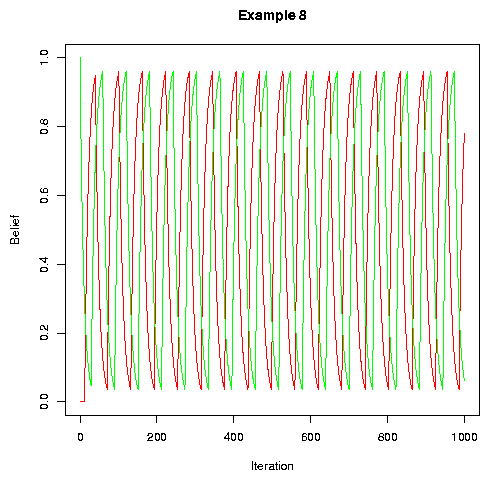 |
Adding noise leads to convergence:
|
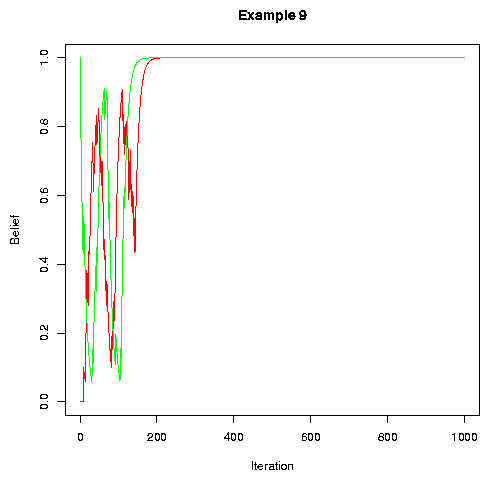 |
So does randomly permuting speakers between turns:
|
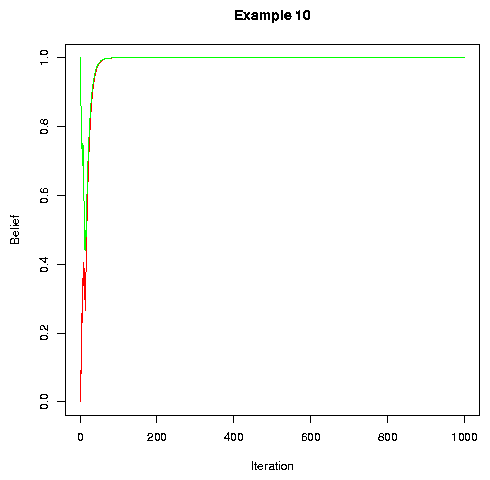 |
Even though there is nothing in these models that pays any attention to keeping words distinct, they do well on this measure of "success", as long as the space of possible words is not filled too full with actual words. The word pronunciations that result from the models tend to sprinkle themselves randomly around the available space, and this normally is enough, since we are putting about roughly 2^14 "morphemes" into a space defined nominally by 20 bits or so (~4 phonemes per word, chosen from a set of ~32 = 4*5=20).
In fact, the facts about homophony in real languages are in rough quantitative agreement with the predictions of a simple model that assumes words are sprinkled randomly in such a space. The graph below compares the growth of homophony with vocabulary size for three models. The curve plotted with X's has words as random binary vectors of 19 bits. The curve plotted with O's has random binary vectors of 20 bits. Both curves are shown for 100 sample points in a vocabulary growing from 1,000 "words" to 100,000 "words". Both curves are upward accelerated, as should be expected, because as the available space fills up, the number of homophones per 1,000 random patterns will increase.
The curve plotted with triangles is English, as represented by a 97,000-word pronouncing dictionary, created by combining a 47K-word dictionary with a 50K proper name list. The resulting dictionary was sorted in random order, and the number of homophones counted for each cumulative subset of the resulting list, from 1,000 to 97,000 items. This procedure somewhat underestimates the number of homophones, for several reasons. Homographic homophones (that is, words that are both spelled and pronounced the same way, like bank of a river and financial bank) did not exist in the original dictionary as separate items. And homophony among American proper names is arguably of a different character from homophony in general vocabulary. Still, the fit to a random binary vector model of about 19 1/2 bits, in terms of degree of homophony, is not too bad.
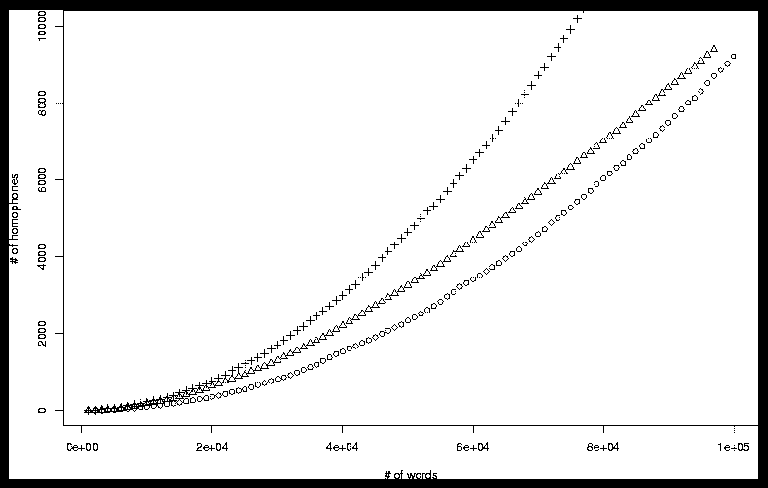
Many other things don't matter to "success", e.g. details of initialization patterns and update staging. As a result, we can conclude that in fact social convergence on word pronunciation is actually not a hard problem after all -- any approach that include "accomodation" (i.e. adjusting internal norms in the direction of current experience) and categorical perception (i.e. interpreting experience digitally) will "succeed" (i.e. will lead to a state in which people's norms are the same, and word pronunciations are mostly different).
But what about using a purely digital representation of belief about pronunciation? What's with these (pseudo-) probabilities? Are they actually important to "success"? In a word, yes. To see this, let's explore a model in which belief about the pronunciation of a word is a binary vector rather than a discrete random variable -- or in more anthropomorphic terms, a string of symbols rather than a probability distribution over strings of symbols.
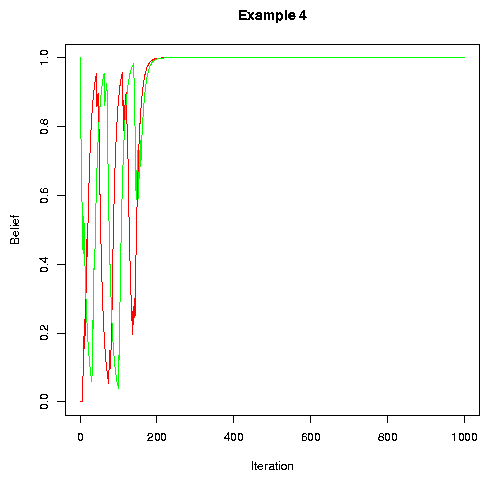
If we have a very regular and reliable arrangement of who speaks to whom when, then success is trivial. Adam tells Eve, Eve tells Cain, Cain tells Abel, and so on. There is a perfect chain of transmission and everyone winds up with Adam's pronunciation.
The trouble is that less regular and reliable conversational patterns, or slightly more complicated ones that are quite regular, tend to result in populations whose lexicons are blinking on and off like Christmas tree lights. Essentially, we wind up playing a sort of Game of Life.
As an example, consider the trivial case of a circular world, permuted randomly after each conversational cycle, with values updated at the end of each cycle so that each speaker copies exactly the pattern of the "previous" speaker on that cycle. Here's the first 5 iterations of a single feature value for a world of 10 speakers. Rows are conversational cycles, columns are speakers. Speakers are listed in "canonical" order.
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
Here's another five iterations after 10,000 cycles -- no signs of convergence:
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
Even if we manage to choose a combination of update algorithm and conversational geometry that converges with categorical beliefs, the result is still likely to be fragile in the face of occasional incursions of rogue pronunciations, as might occur through speech errors if for no other reason.
Some apparent generalizations:
The "doubly digital" character of speech is important -- words are discrete entities, and so are the phonological elements that define their claims on sound. In particular, the perception of a particular instance of the pronunciation of a word must assign its distinctive features to discrete categories, if a speech community is to converge on a shared pronouncing dictionary. At the same time, the representation of word pronunciation in each individual's memory needs to be probabilistic rather than categorical -- a distribution over possible pronunciation instances, not a single particular target pronunciation.
More succinctly: knowledge of word pronunciation is a discrete random variable.
(This may be going too far: the only thing that really matters is that we should be able to learn by "leaky" integration. This permits different members of the "community" to converge trivially to a common value).
There is a perception/production asymmetry: perception must be digital, but production need not be -- and in fact things may work better if it is not. This requirement of quantized ("categorical") perception is an interesting example of converging requirements. It has long be observed that accurate transmission of a large vocabulary requires a system like natural language phonology, in which (the acoustic categorization of) a word is not an arbitrary holistic noise, but rather a combination of signaling elements in which the information load on each element is at most a few bits. I've argued here that perceptual assignment of word pronunciations to a set of independent, discrete categories may be a necessary condition for "group learning" of vocabularies that are socially emergent rather than genetically fixed. A phonological system solves both problems.
There are innumerable crucial things about speech and language that have not been addressed at all in this modeling exercise. Nevertheless, the properties of these excruciatingly simple models may cast some light on the problems that our species' approach to speech and language has evolved to solve. The next (and perhaps more interesting) step will be to explore the ways in which a system with the required characteristics could have evolved -- while still accounting for the fact that such systems do not seem to have evolved very often.