Random letter-partition advantages in baby names
« previous post | next post »
Commenting on "QWERTY again", 5/14/2014, Rubrick suggested that
It seems like an extremely simple way to check the validity of this theory would be to repeat the analysis, but with the letters grouped into two random subsets, rather than right-left subsets. In fact, I'd think the original authors should have done this as a control. If this new grouping yields a graph with any meaningful-looking trends whatsoever (or if multiple repeats of the analysis with different random subsets yield such trends a significant percentage of the time), it would pretty soundly deflate the idea that the original trends are the result of "right-hand favoritism".
Steve Kass followed up on this suggestion, providing five examples, and commenting that
The graphs don't all look the same, but they all look interesting, and several of them practically beckon the storyteller. There's something interesting about this general kind of data and "advantage function" analysis worth discovering, I think.
A bit later, Breffni countered that
[I]n fairness to these researchers, they didn't go from pictures to story. They put this QWERTY effect theory on record in previous publications, and adduced evidence in support of it (whatever you think of that evidence); the theory leads to a clear-cut hypothesis regarding trends in baby names; and the hypothesis is indeed supported.
And Steve responded by quoting the Casasanto et al. paper:
"In Experiment 5, we tested whether the first names that Americans give their children have changed over time, as QWERTY has become ubiquitous in people’s homes, and whether new names coined after the popularization of QWERTY are spelled using more right-side letters (i.e., have a greater RSA) than names coined earlier."
and arguing that
This is not a clear-cut hypothesis, at least not clear-cut in the sense that you could state it and there would be little doubt what mathematical proposition about data it hypothesized.
Obviously it's a well established fact that "the first names that Americans give their children have changed over time", both before and after "QWERTY has become ubiquitous in people's homes" — a hypothesis framed in those terms is guaranteed to be supported by the data. Breffni took a more charitable interpretation, namely that the change should be in the direction of greater "right side advantage" over the past 20-odd years; and I agree that this seems to be what the authors had in mind, and indeed what they found.
Steve objects to the idea looking for a slope significantly greater than 0 is a valid way to test such a hypothesis, at least in the sense that the "p value" has any meaning; and extrapolating from his five random-partition experiments, he suggests a "metahypothesis" like
Let M be any measurement on words that is computed as a sum over the letters of the word of a function on the letters A to Z that has value between -1 and 1. Then the mean value of M on the 802 baby names in significant use since 1960 has probably been trending in the same direction for at least 15 years.
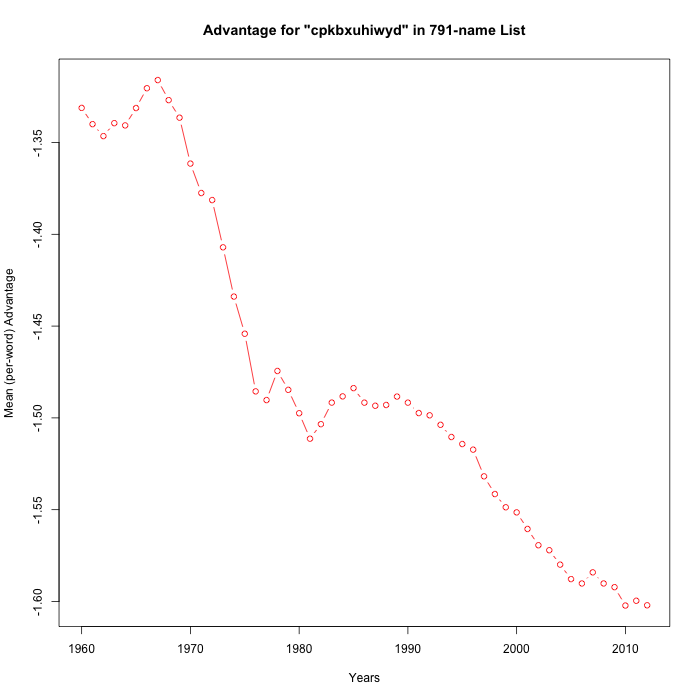
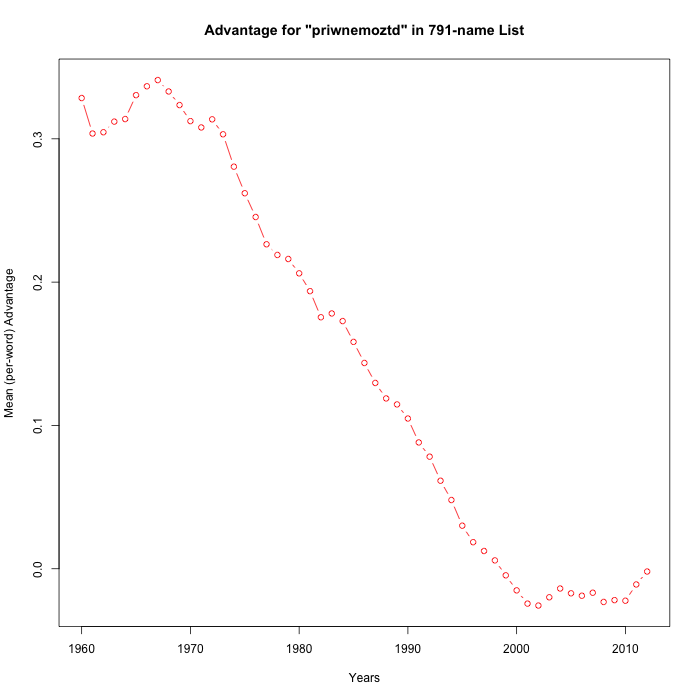
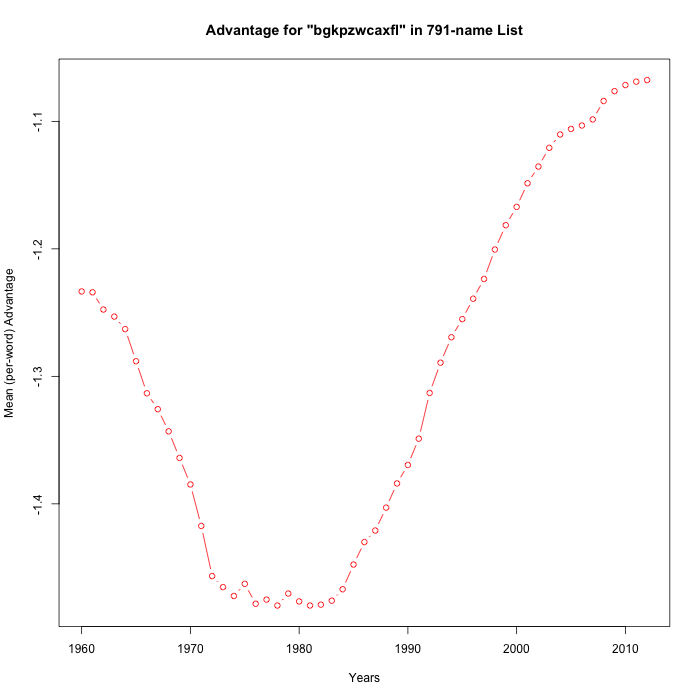
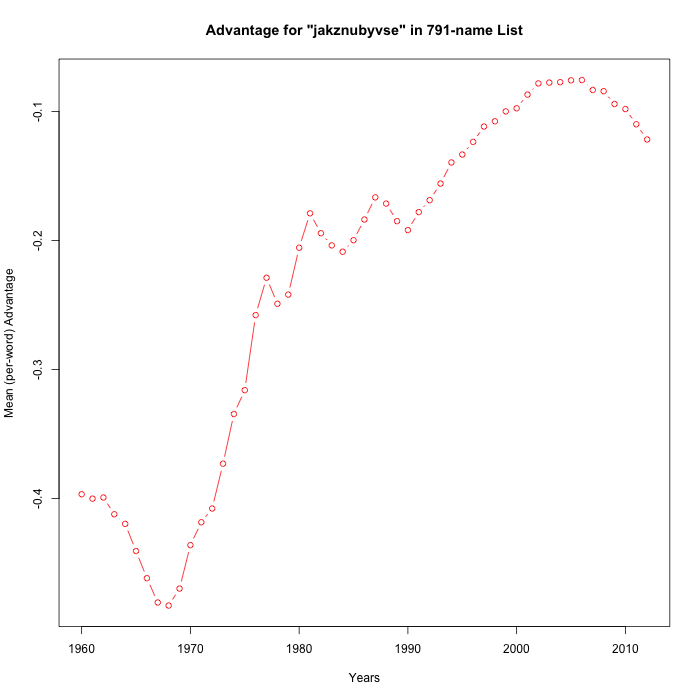
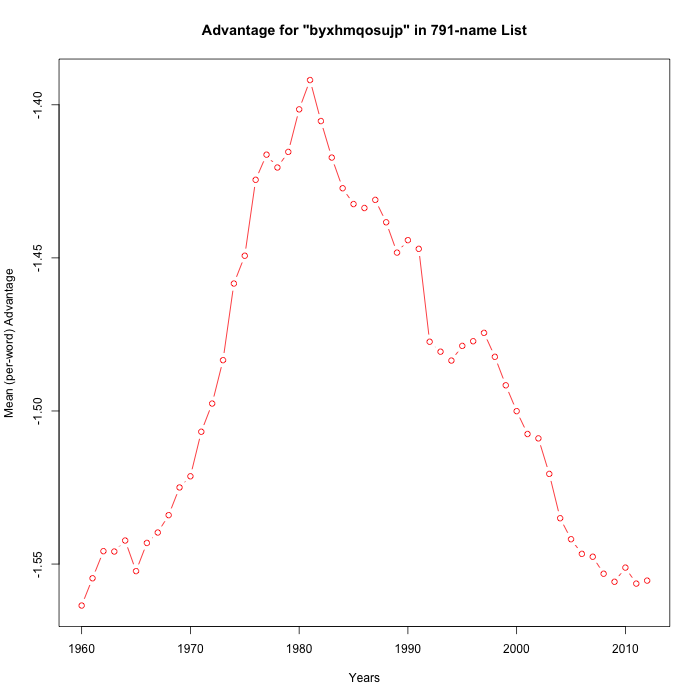
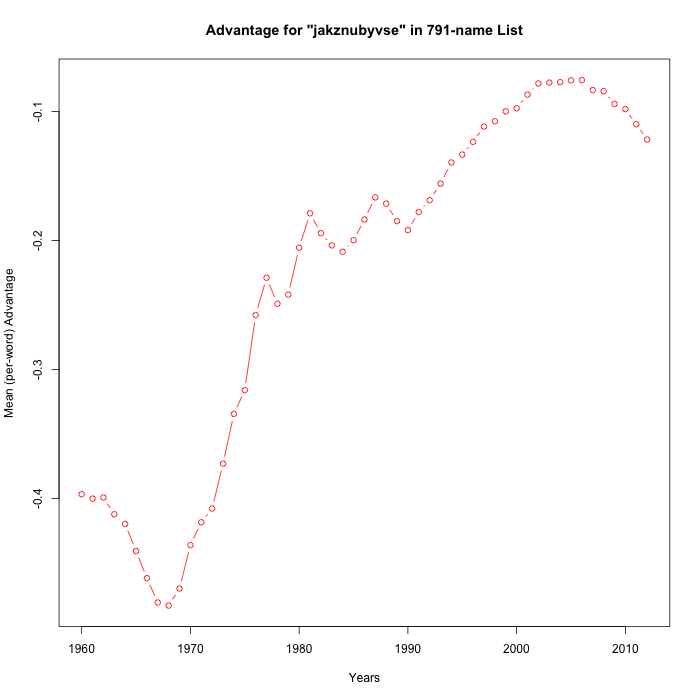
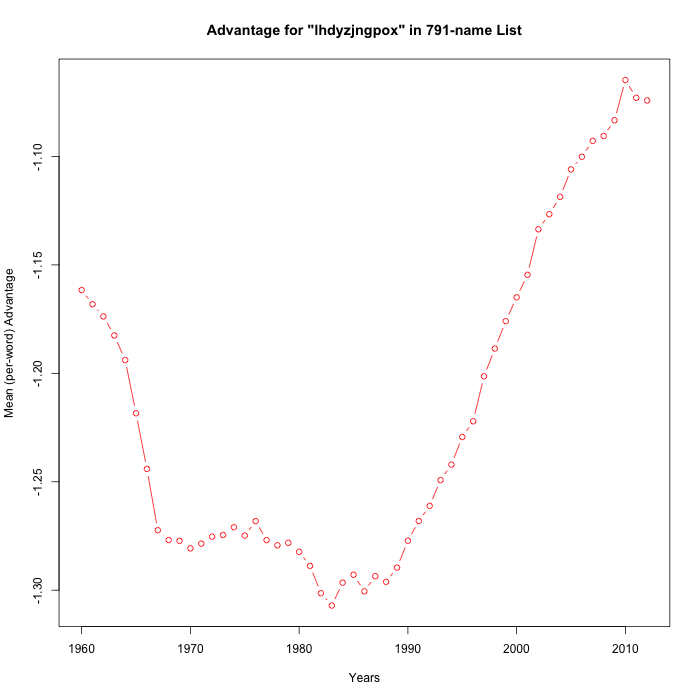
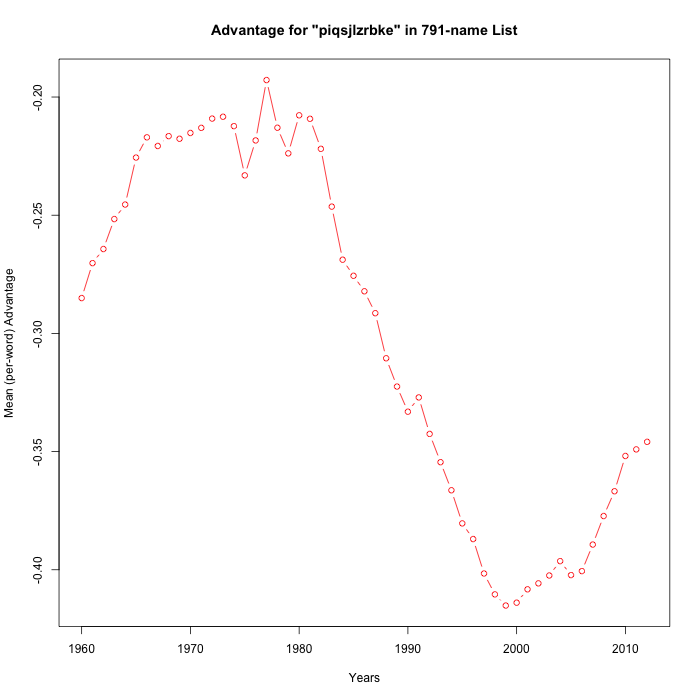
In order to facilitate empirical exploration of such metahypotheses, I wrote a simple program to generate random partitions of the alphabet into 11-against-15 subsets, and to check the random-subset-advantage (averaged by name) against the SSA's baby-name data from 1960 to 2012.
(If you want to continue the recipe at home, and have access to a unix or unix-like environment, my programs are linked and described at the bottom of this post.)
Here are ten runs:
 |
 |
 |
 |
 |
 |
 |
 |
 |
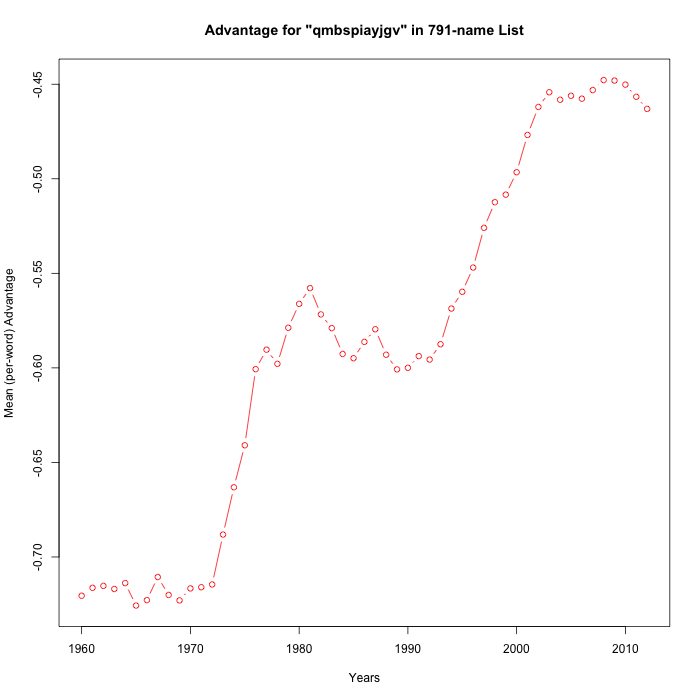 |
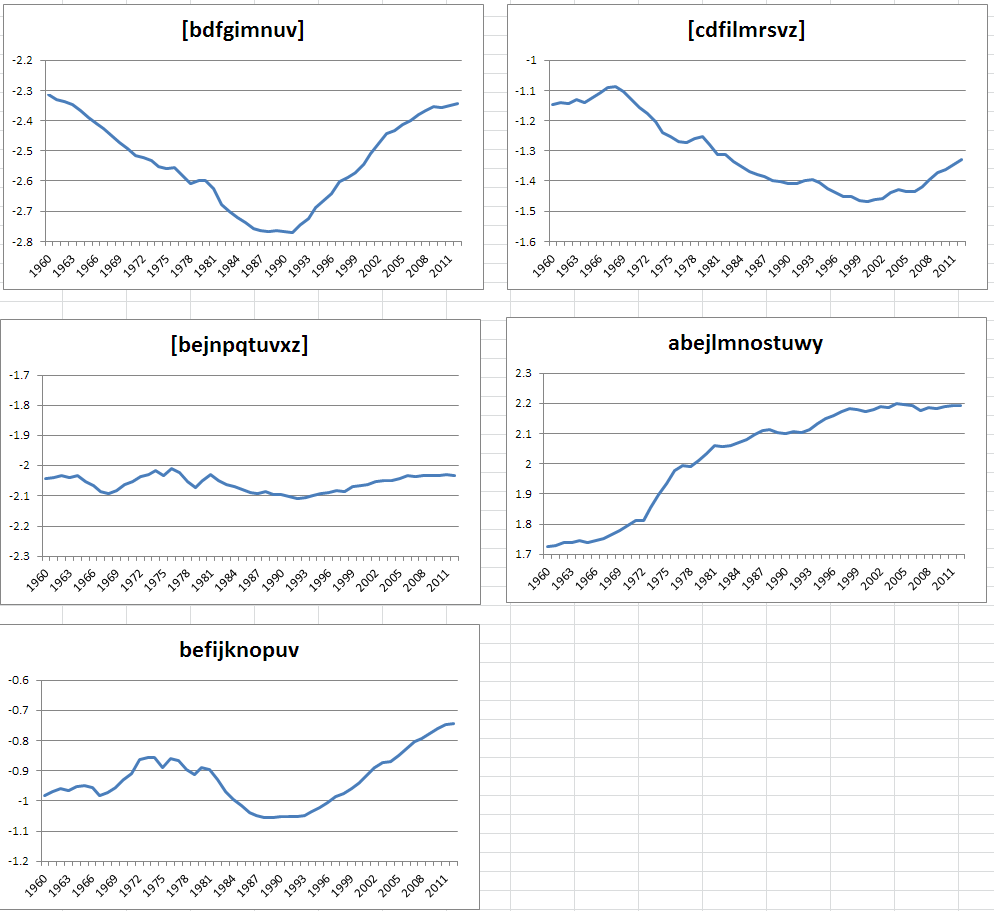
And here are Steve's five examples again:
It's not exactly the meta-analysis that Steve asked for, but 8 of these 15 random trials have "statistically significant" positive slopes over the period 1990-2012. So I'd respond to Breffni's cogent observation by guessing that Casasanto et al. in fact had about a 50-50 chance of being correct — maybe a bit better since they could have adjusted their estimate of when "the popularization of QWERTY" occurred.
And I wonder whether they would have reported this experiment if the results had been equivocal or negative. They could have found plenty of good reasons for concluding that baby-name changes are not a valid test of their ideas.
Mainly, I agree with Steve that there is an interesting mathematical point lurking in these graphs, not specifically connected to baby names or QWERTY handedness. More on that at some future time.
RECIPE: As discussed in the previous post, neither Steve nor I were able to reproduce Casasanto et al.'s count of 788 names that occurred 100 or more times in every year from 1960 to 2012. On different interpretations of the definitions, we came up with sets of 802 names and 791 names. In what follows, I'm using the list of 791.
The basic data from the SSA is here — when you unzip that archive, you'll find 134 csv files of the form "yobNNNN.txt", where NNNN is a year from 1880 to 2013. You can run this script to create corresponding files "100yobNNNN.txt" that are limited to the names that occurred 100 or more times in the years 1960-2012. (If this strikes you as an unnecessary restriction, you can adjust the following script appropriately.)
Then each time you run this script, it will create a new random 11-to-15 partition, and run it over the years 1960 to 2012 in order to create an analogue of the "right side advantage" time function. You'll need this randperm (perl) function, and the file alphabet.
Finally, (a modified version of) this R script will create the graphs — note that you will have to change the list of random letter-sets to correspond to the results of your experiments.
unekdoud said,
May 17, 2014 @ 11:55 am
This might be a little simplistic, but why not just count the letters (by ratio) and look for (excessively huge) correlations? That way, it might be easier to identify which letters are responsible for the RSA trend. It may also be a good way to handle Steve's vowel advantage calculation, as well as for specific partitions such as top-row-advantage.
D.O. said,
May 17, 2014 @ 12:02 pm
The mathematical basis for all of this is the same or very similar to the factor analysis or maybe to the analysis of the factor analysis.
D.O. said,
May 17, 2014 @ 12:22 pm
@unekdoud. I did just that, but not for all years just a change from 1990 to 2010. Here's the table of the regression on the year coefficients for all letters (all letters of all names in the SSA database). Numbers are normalized such that if a new letter (say ъ) was introduced in 1991 and rose in popularity linearly until in 2010 all names consisted of ъ only (in other words were like Ъъъъ, Ъъъ) the coefficient would be 100 (to save space).
a 4.41 j 1.21 s -2.57
b -0.04 k 0.39 t -2.12
c -2.50 l -1.10 u -0.03
d -2.18 m 0.39 v -0.11
e 1.04 n 0.76 w -0.19
f -0.25 o 0.11 x 0.18
g -0.04 p -0.11 y 0.77
h 0.51 q -0.42 z 1.76
i 0.66 r -0.54
Enjoy.
Jerry Friedman said,
May 17, 2014 @ 12:32 pm
Graphs of baby names tend to have rather steady ups and downs. I'd have thought this feature of the data was a key to the trends in the graphs above.
Another guess: If the QWERTY effect is responsible, then the left-right partition of letters will have the steepest increase or one of the steepest ones, and other partitions that have steep increases will be close to it. If not, there could be partitions of letters that have significantly more dramatic behavior in the last few decades than the left-right partition, and there could be some that aren't related to QWERTY but at least as dramatic. Does that make sense? I don't have time right now to even look at the left-right distributions of the partitions that Steve Kass and MYL have tried, but maybe in a few days.
I suppose a better test of the QWERTY hypothesis would be to survey parents and their keyboard use, but that would be a lot harder.
Marek said,
May 17, 2014 @ 12:38 pm
I admit I haven't followed the whole story, but presumably data on baby name trends from countries using layouts alternative to QWERTY could also be used to double-check claims like this? For instance (apparently, going with a cursory search of Wikipedia here), Korean keyboards follow a completely different scheme for Hangul, as do the most widely adopted Cyrillic keyboards in Russia.
Jerry Friedman said,
May 17, 2014 @ 12:59 pm
Okay, does anyone want to run aehijkmnxyz vs. bcdfglopqrstuvw? Those are split according to D.O.'s, values, most positive in the first set. That is, if anyone can see any value in the exercise.
D.O. said,
May 17, 2014 @ 1:01 pm
Sorry, made a stupid mistake. Correct table.
a 2.97 j -1.99 s -1.76
b -1.27 k -1.25 t -2.30
c -1.91 l 2.32 u 0.04
d -1.79 m -0.86 v -0.01
e 2.33 n 0.64 w -0.14
f 0.14 o 0.89 x 0.28
g 1.64 p 0.09 y 0.34
h 0.65 q 0.02 z 0.38
i 1.90 r -1.38
Keith M Ellis said,
May 17, 2014 @ 11:35 pm
In a post to his blog today, statistician Andrew Gelman quotes himself (from this response to a paper published in Ecology):
I'm not a statistician, mathematician, linguist, psychologist, or a cognitive scientist. I'm not even an academic and certainly have no expertise in these matters.
But having read Gelman for several years, and having read Liberman's frequent critiques of shaky conclusions using minimal or poorly utilized statistical techniques, and from more generally following (as best I can) this long-running debate about the misuse of p-values (and especially in psychology, I think), it seems to me that there's very much a pattern here and the work that's the subject of this post is of a piece with it.
That there was statistical significance found was, as far as I can tell and as implied by this post and previously by Kass, misunderstood as a validation of the authors' hypothesis even though that significance could mean a great many different things. And, really, their hypothesis wasn't tested, which is what I think Kass has been arguing.
Steve Kass said,
May 17, 2014 @ 11:45 pm
It’s pretty darn good. Thanks for following up!
Lance Nathan said,
May 18, 2014 @ 12:15 am
I was curious to try this for myself, using a few functions that don't quite fall into Steve's metahypothesis. My Python code is here for anyone who wants to verify that I was doing the right thing; my resulting graphs are here. When I ran it on the same set of 802 names as Mark, I definitely reproduced something that looked very much like the graph from the original paper (though like Mark's, it was somewhat vertically offset, so my function wasn't perfect). This is the first graph in the linked picture.
Then I ran the same code on a different function, "centrality", which assigned a number from 0 to 12 to each letter depending on how far the letter is from the center of the alphabet (0 for m and n; 12 for a and z). The variation occurs in a smaller range, but there's an obvious trend, and as Steve meta-hypothesized it's been consistently downward for the last 20 years. (Admittedly, left-hand letters are on average farther from the center of the alphabet than right-hand letters, so this may just reflect the same kind of trend that Jasmin and Casasanto found–but it also presents an alternate possibility, namely that people are subliminally concerned by how alphacentric their children's names are!) This is the second graph.
Finally, I tried a metric that seemed singularly unlikely to influence anyone's naming decisions, no matter how subliminally: I assigned 1 to names whose letters sum to an even number (using A=1, B=2, …, Z=26), and -1 to names whose letters sum to an odd number. The results are in the third graph, and I think they're particularly dramatic. They definitely tell us something about naming trends…though at this point I think what they're telling us is that names trend over time, and almost any mathematical transformation on names will demonstrate that.
Steve Kass said,
May 18, 2014 @ 12:30 am
@Jerry Friedman: Here’s a graph of the weighted mean aehijkmnxyz-advantage by year for the 802-name collection: http://i.imgur.com/V4JuadS.png Is this what you wanted?
Americans have been giving babies names with increasing annual weighted average aehijkmnxyz-advantage steadily since 1982. From 1960-1981, there was no steady trend, and the change in behavior at 1982 is visually striking.
[(myl) Perhaps because the IBM PC came out in 1981? ;-) ]
The features of this graph are similar to those of random letter partitions analyzed by Mark and me, so if anything, this suggests that the the strength of the effect of a partition on features in the average-advantage graph may not be predictably high based on straightforward caculations about the data set in questioh.
a George said,
May 18, 2014 @ 2:51 pm
so, only computer-literate AND wealthy parents beget children?
Jerry Friedman said,
May 18, 2014 @ 6:54 pm
Steve Kass: Thanks! Unfortunately, since D. O. corrected his results, the partition I want is aefghilnopquxyz vs. bcdjkmrstvw. But only if you find some interest in it.
J.W. Brewer said,
May 18, 2014 @ 8:12 pm
Thanks to the internet, researchers now have an important new dataset of subjective female perceptions of the valences of various common male given names http://www.buzzfeed.com/summeranne/gentle-lucases It probably needs to be appropriately turned from cut-and-pasted text into some sort of quantitative metric, but once numerical values are assigned to the names, you can run all of these different alphabet partitions on it and see what best accounts for the data.
Jerry Friedman said,
May 18, 2014 @ 10:46 pm
I said "his" with reference to D.O., but actually I don't know what pronoun is appropriate. Sorry if I caused any offense.
Steve Kass said,
May 18, 2014 @ 10:54 pm
@Jerry: Will do when I get a chance.
Mark: Have you measured the correlation of random-letter partition advantage vs. "valence" of the words in ANEW? I'm on the road for a week without my ANEW and DANEW databases handy, but I'll try to run some tests when I"m back.
Steve (RSA = -5 and proud of it.)
Breffni said,
May 19, 2014 @ 3:37 am
Well, I'm entirely convinced by the Rubrick/Kass/Liberman rebuttal.
Andrew Bay said,
May 19, 2014 @ 7:37 am
Can we have a "control" of "A-K, L-Z" split? Why does it have to be random?
JW Mason said,
May 19, 2014 @ 1:42 pm
So for those of us who work or teach in fields prone to misuse of statistics, what's the best way of discouraging this kind of thing? If one were, let's say, teaching an introductory econometrics class, is there any reading one could assign to try to prevent students from growing up to be Jasmins and Casasantos?
[(myl) I feel that this comment is unfair to the authors, who have given us a multi-dimensional empirical investigation of an interesting and non-obvious idea. Their statistical methodology is in line with the standards of their field, as far as I understand it. The questions that I and others raised with respect to the earlier work mainly had to do with exaggeration in the popular press of the effect size, which was not their fault, and with the question of whether the effect could be replicated with other word-valence datasets, which is a normal sort of follow-up in work of this sort. The new paper offers a number of independent replications, which is perfectly proper. The inferential issues in the baby-names work are complicated and somewhat sui generis, so it's not surprising that the authors should have missed an approach that calls their results into question.
Overall it seems to me that we need more researchers like Casasanto and Jasmin, whether I agree with their conclusions in this particular case or not.
One general answer to (a less ad-hominem form of) your question would be: Less reliance on traditional "statistical significance" calculations, and more exploration of various simulations or generative modeling scenarios.]
Lance Nathan said,
May 19, 2014 @ 8:54 pm
@JW: try http://www.tylervigen.com/ .
Steve Kass said,
May 19, 2014 @ 10:47 pm
That's an outstanding question that deserves a much more thoughtful answer than I could possibly give here and now. I'll try to collect some thoughts and get back to you here and via gmail. And if you do, implausible as it seems from the rest of your bio, live in Brooklyn, maybe we can sit down some time and see if we can come up with an answer.
JW Mason said,
May 20, 2014 @ 9:07 am
Steve,
Just moved back to Brooklyn. (I'll be teaching at CUNY.) I should update the bio on my blog. And yes, please do email me — it's a real question.