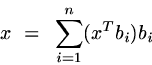 (Equation
1)
(Equation
1)We start with a set of high-dimensional observations (e.g. pictures of faces, EEG recordings, etc.). The general idea is to find a "natural" set of coordinates for this body of data, and to use this to produce a reduced-dimensional representation by linear projection into a subspace. Location in the subspace is then used as a basis for measuring similarity, assigning to categories, or whatever. The motivation for the dimension reduction may be efficiency (less memory, faster calculations), or better statistical estimation (e.g. of distributions by observation type), or both.
A new set of coordinates (for an N-dimensional vector space) is equivalent to a set of N orthonormal basis vectors b1 ... bn. We can transform a vector x to the new coordinate system by multiplying x by a matrix B whose rows are the basis vectors: c = Bx. We can think of the elements of c as the values of x on the new dimensions -- or we can think of them as "coefficients" telling us how to get x back as a linear combination of the basis vectors b1 ... bn.
In matrix terms, x = B'c, since the basis vectors will be columns in B', and the expression B'c will give us a linear combination of the columns of B' using c as the weights. (Note: to keep the gifs down, we're using ' to mean transpose in the body of the text here).
So far this seems pretty trivial -- we've shown that we can represent x as x = B'Bx, where B is an orthogonal matrix (and hence its inverse is its transpose).
We can re-express this in non-matrix terms as
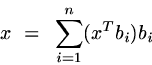 (Equation
1)
(Equation
1)
This is equation is known as the Fourier expansion, for reasons that will become clear next week (if you don't already know it). For a given orthonormal basis, the coefficients are unique -- there is a unique way to represent an arbitrary x as a linear combination of the basis vectors B. (In Fourier analysis, the basis vectors are sinusoids -- but nothing about equation 1 requires this choice).
Let's spend a minute on the relationship of equation 1 to the matrix form x = B'Bx. The subexpression Bx, which is giving us the vector of "coefficients" (i.e. the new coordinates), is equivalent to the subexpression read "x transpose times b sub i", which is giving us a single coefficient for each value of the index i. Spend a couple of minutes to make sure that you understand why these two equations mean the same thing.
If we truncate Equation 1 after p terms (p < N), we get
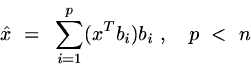 (Equation
2)
(Equation
2)
We are thus approximating x as a linear combination of some subset of orthogonal basis vectors -- we are projecting it into a p-dimensional subspace. Obviously each choice of p orthonormal vectors gives a different approximation. Within this general range of approaches, there are a lot of alternative criteria that have been used for choosing the set of basis vectors. Oja (Subspace Methods of Pattern Recognition, 1983) gives six:
There are others in the more recent literature as well.
Criterion no. 4 gives rise to Principal Components Analysis. Criterion no. 1 gives rise to the Karhunen-Loeve Transform.
For Principal Components Analysis, the orthonormal basis set is given by the eigenvectors of the covariance matrix of the observation vectors x. Since a covariance matrix is real and symmetric, it's guaranteed that the eigenvectors can be chosen orthonormal.
Here is a sketch of why this works. For the first basis vector, we want to find a linear combination of the elements of observation vectors x that will have maximum variance, in other words to find a fixed weighting vector u such that
E((x'u - E(x'u))^2) = maximum (across all observations x)
With a little algebra, this develops as:
E((u'(x-Ex))^2) = u'E((x-Ex)(x-Ex)')u = u'Ru
where R is the covariance matrix of x, and we want u'u =1 (so that u is of unit length). The solution will be the unit eigenvector of R with the highest eigenvalue (for which the value of u'Ru will obviously be that eigenvalue).
This is a simple (but surprisingly effective) application of these ideas by Turk and Pentland ("Eigenfaces for Recognition," J. Neuroscience, 3(1), 1991).
You can see a recent implementation on the MIT Media Lab face recognition demo page.
We start with m q x q pixel images, each arranged as an n=(q^2)-element vector by stringing the pixel values out in row ordering, starting from the upper left of the image. This is the standard way of treating images as vectors. Call these image vectors G1 ... Gm. Note that n will be fairly large: e.g. if q = 256, n = 65,536.
Calculate the "average face" F -- just the element-wise average pixel value -- and subtract it out from all the images, producing a set of mean-corrected image vectors H1 ... Hm = G1-F ... Gm-F.
Calculate the covariance matrix C of the mean-corrected images. If L = is an n x m matrix whose columns are the images H1 ... HM, then C = (1/m) LL' (an n-by-n matrix). The normalization by 1/m is not essential -- look through the development below and see if you can figure out why.
Calculate the SVD of C = USU'. The columns of U will be the n-element eigenvectors ("eigenfaces") of the face space. The coefficients of an image x will be calculated by taking the inner product of the columns of U with x. This is an instance of equation 2 above, given that we truncate the expansion at p < n eigenvectors.
Digression: it may be too costly to do this directly, since if n = 65,536, then C is 65,536 x 65,536. As a practical expedient, we can take another route to getting (some of) the eigenvectors. Basically, instead of taking the SVD of C = LL', we take the SVD of L'L (which is only of size m x m, where m is the number of images in our "training set," say a few thousand). Then consider the following:
L'L = WTW'
LL'LL' = LWTW'L'
(LL')^2 = (LW)T(LW)'
Finally, form a face subspace by taking the p most significant eigenvectors. The projection coefficients for any face Gi are just the inner products of the (mean-corrected) face with these eigenvectors. A compact representation of G is just its P projection coefficients.
We can then define a similarity metric as Euclidean distance in the subspace, and use this metric for recognition.
Take a look at photobook, an interactive demonstration of eigenfaces recognition.
An alternative method called fisherfaces, which also projects the image space linearly to a low-dimensional subspace.