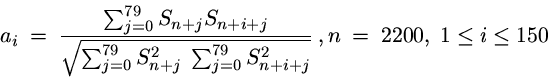CIS 558 / Linguistics 525
Computer Analysis and Modeling of Biological Signals and Systems
Homework 1

Due: 2/5/1999

This set of exercises corresponds roughly to the first two items in the syllabus. Thus it is due at the end of the fourth week of the course. However, it is strongly suggested that you begin earlier, doing one section each week.. If you run into any troubles, either technical or conceptual, please contact me.

The Matlab instructions are for Unix, and specifically for the (clients of) unagi.cis. If you are doing the homework in one of the PC labs, or elsewhere on campus, contact me in advance in order to ensure that the needed data files are available to you, and that any necessary changes in instructions are specified.

In order to access the referenced Matlab objects, make a directory ~/matlab (in your home directory), create a file called startup.m in your matlab directory, and add to it a line such as 

path(path,'/mnt/unagi/speech/matlab')

Except for section III, questions 1 and 2, your answers should be in the form of a file that can be executed directly by Matlab. Please check that your file can actually be executed before submitting it. Email your solutions to myl@unagi.cis. If you want to add any commentary, use the comment character % to do so. For III/1-2, your answer can be in the form of Matlab comments; Matlab code for this case is optional.

I. Using MATLAB

A. Basic 1D operations in MATLAB

  1. The file audio1.mat contains 10,399 numbers representing about 1.3 seconds of a sound waveform sampled 8,000 times a second, assigned to a variable named S. Load it using the command load('audio1')

    Now plot the vector S. Use the Matlab function plot. You can execute help plot to get information on this function.

  2. Given that S is sampled at 8 KHz, with the first sample representing time 1/8000 and the 8000th sample representing time 1, create a second vector of the samples spanning the time period from .275 to .325 seconds inclusive. Plot it. Keep in mind that putting a semicolon after a MATLAB expression will prevent its value from being printed.
  3. Create a third vector corresponding to the 10399 samples of S scaled so that the minimum value is -1 and the maximum value is 1.
  4. Calculate the serial cross-correlation of 80-sample pieces of S, starting at sample 2200, for lags between 1 and 150 samples inclusive. In other words, calculate a vector A such that

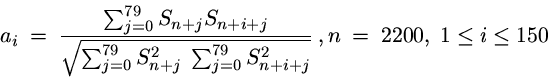
    \begin{displaymath} \displaystyle a_i ~=~ \frac{\sum_{j=0}^{79}{ S_{n+j} S_{n+i+... ... ~ \sum_{j=0}^{79} S_{n+i+j}^2}} ~, n~=~2200, ~1 \le i \le 150\end{displaymath}

    You can do this using the MATLABfor loop and the functions sum and sqrt. More efficiently, try to use your knowledge of linear algebra (inner products, vector lengths)!

    As the nomenclature implies, you are calculating the correlation of a piece of S with another piece of S at a variety of offsets. Calculations of this kind are used in periodicity detection. Keep in mind that Matlab's vector indices start with 1 rather than 0.

  5. What is the maximum value of A? For what index value does it occur? Use help max to see how to find this out.
  6. Plot A three times, first with the X axis in samples; second with the X axis in seconds (i.e. samples/8000); and third with the X axis in Hertz (the inverse of the measure in seconds). In the last case, limit the range of values shown to 500 Hz. and below.
  7. [Extra Credit] Calculate a version of A based only on the numerator of the equation given (i.e. based only on the inner products of an 80-element stretch of S with 150 other 80-element stretches of S. Is the maximum at a different place?

B. Basic 2D operations in MATLAB

The following problems pertain to image-processing in Matlab. An image is stored as a two-dimensional matrix, and displayed with the command image. The elements of the image are typically called ``pixels''. A modified version called imagesc will scale the pixel values so that the largest is mapped to white and the smallest to black.

Execute the following to load an image into Matlab from the course directory: 

fid = fopen('einstein.raw','r')
al = fread(fid,[256,256],'uchar')';
fclose(fid)

Now display the image using imagesc. You may also have to execute the expression colormap(gray).

  1. Select a subimage of al with vertical indices in the range 70-120 and horizontal indices in the range 80-130. This operation is commonly refered to as ``cropping''. Display the subimage. Note that even though the subimage is smaller than the original, it is displayed as being the same size (Note: you can use the command size to determine the actual size of the underlying pixel array). Why is this? What happens when you resize the Matlab figure window?
  2. Create an image containing every fourth pixel (in both the horizontal and vertical directions). This operation is known as ``subsampling'' (Hint: check the help information for colon).
  3. Create a vector containing the 25th row of al. Plot it.
  4. Compute the minimum and maximum values of al. At what locations do these occur? Plot a histogram (essentially, a probability distribution) for the pixel values of al using the Matlab function hist.
  5. Matlab allows us to operate on images point-by-point. Compute (and display) a new image whose pixels are the square root of the pixels of al. Look at the histogram and compare it to that of al (you may want to execute the command figure(2) to put this in another window). Compute and display an image containing a pixel of value 1 at locations where al is greater than 128, and 0 elsewhere.
  6. Load another image from the file 'reagan.raw' in the course directory. Compute images that are the sum and product (pointwise!) of this image and al.

II. Color Matching

Execute the command load('colmatch.mat') in your Matlab environment. This file contains a number of matrices and vectors related to the color matching problems discussed in class. In particular, the variable P is an N x 3 matrix containing wavelength spectra for three basis lights (``primaries''), and the variable M is a 3 x N color-matching matrix corresponding to these primaries. For these problems N=31, corresponding to samples of the wavelength spectrum from 400nm to 700nm in increments of 10nm.

Set the variable light to a random vector of length 31. We will consider the components of this vector to be samples of the wavelength spectrum of a particular light.

  1. What combination of the three primaries in P will match the appearance of this randomly chosen test light? Compute the wavelength spectrum of the matching light (as a linear combination of the three primary wavelength spectra) and compare it to that of the test light. Why is it different?
  2. The variable Palt contains a different set of primary lights. Compute the corresponding matching matrix Malt (you will probably need to make use of the Matlab function inv which computes the inverse of a square matrix). Repeat the previous exercise with Palt and Malt. Is the matching spectrum different than in the previous exercise?
  3. The variable Phosphors contains the emission spectra of three standard color monitor phosphors. How would you choose the amplitude of each phosphor's emission in order to produce light on the monitor that matches light? Compute these amplitudes and demonstrate that the resulting mixture of phosphors does indeed produce the same tri-stimulus coordinates in the matching experiment.
  4. The variable M2 contains yet another matching matrix. This one was computed for a color-impaired individual, using the primaries in P. Compute the SVD of M2. How can you tell this individual is color-impaired? Assume that the individual has a standard color-blindness problem: they are missing one or more cone types. Derive the spectral sensitivity of the missing (or remaining) cone.
  5. The variable Cones contains approximate spectral sensitivities of t he three color photoreceptors (cones) in the human eye. They are ordered such that Cones(1,:) corresponds to the L (long-wavelength, or red) cones, Cones(2,:) the M (green) cones, and Cones(3,:) the S (blue) cones. Plot these using plot or try rgbplot, and compare to the cone sensitivity vector you derived in the previous problem. Which cone was missing from (or remaining in) your color-blind subject?
  6. Having just purchased a new house in Center City, you decide to paint the baseboard trim a new color. In particular, you'd like to have the trim match the color of your new couch (chartreuse, of course). You make a trip to the paint store, carrying with you a sample piece of fabric (complete with plastic slipcover). The store carries two brands of paint: ShabbyTint, which is mixed from three primary colors, and RichTone, which is mixed from a set of six primary colors. Naturally, the RichTone costs four times as much, so you decide to go with the ShabbyTint, and quickly pick a matching color from the ShabbyTint paint chart (the store mixes it for you, from the three ShabbyTint primaries).

    Load the file paint.mat into Matlab. This will define a few variables:


    1. Determine the mixture of ShabbyTint primaries that will match the sample you've taken to the paint store. Assume that paint-mixing is additive (it really isn't!). Plot the wavelength spectra of the sample and the paint (when viewed in the paint store) on the same plot (use the Matlab hold command to do this). Demonstrate that a paint mixed from this proportion of the three primaries will look just like the sample.
    2. You may now view these colors on your monitor. Create two column vectors of height 3, called rgb1 and rgb2 containing the monitor gun values (proportion of each phosphor) to be used to display a color matching the couch and the shabby paint mixture under fluorescent lighting. You should assume that the matrix Phosphors contains emission spectra that are correct for your monitor (this may not be true). Then call the function showcols(rgb1,rgb2).
    3. You take the paint home, and paint a small sample of baseboard. The next morning, when the sun comes up, you find to your horror that the baseboard doesn't match the couch at all. What happened? Show that the two colors really don't match when viewed under daylight. Render them on the screen using showcols to check this.
    4. What is the best (least-squares) combination of ShabbyTint primaries that you could have used to match the couch both in daylight and incandescent light?
    5. What if you use the RichTone paint? Assess the quality of the best-matching mixture under both daylight and fluorescent light.

III. Linear Shift-Invariant Systems

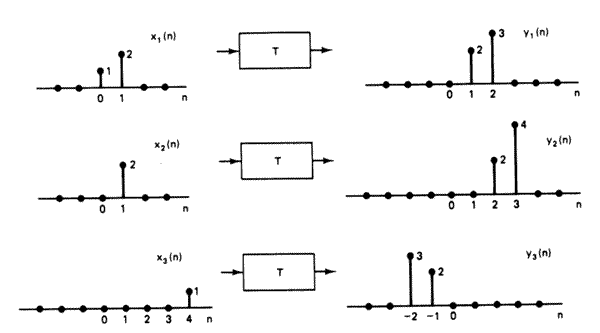
  1. (Oppenheim and Shafer 1989 p. 68). The system T in the figure below is known to be time-invariant. When the inputs to the system are x1[n], x2[n] and x3[n], the responses of the system are y1[n], y2[n], y3[n] respectively.
    1. Could the system T be linear? Explain.
    2. If the input x[n] to the system T is delta[n] (i.e. a unit impulse at time 0), what is the system response y[n]?
    3. Determine all possible inputs x[n] for which the response of the system T can be determined from the given information alone.


     

  2. (Oppenheim & Shafer 1989 p. 69) The system L in the figure below is known to be linear. When the inputs to the system are x1[n], x2[n], x3[n], the response is y1[n], y2[n], y3[n] respectively.
    1. Could the system L be time-invariant? Explain.
    2. If the input x[n] to the system is delta[n], what is the system response?


     

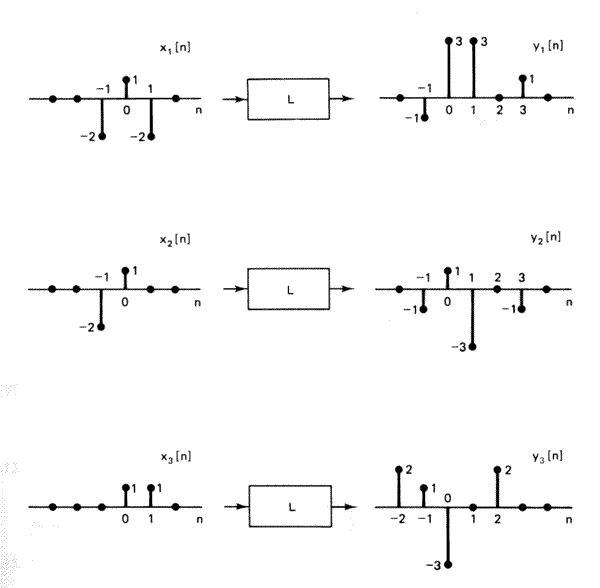
  3. Create a vector of length 24 containing an impulse at location 5, a step edge at location 12, and a unit-slope ramp starting from location 18. Convolve this signal with the ``two-point averager'': [0.5, 0.5], and the ``two-point differencer'': [0.5,-0.5]. How does the differencer respond to the various features?
  4. Show that the two convolution results computed above may be added together to reconstruct the original signal. Would this be true for an arbitrary input signal?
  5. Write a Matlab function mksine to construct a vector of samples of a sine function. The function should take arguments size, period, amplitude, and phase. The phase should be measured from the first sample (that is, the first sample is at the origin).
  6. Compute the convolution of each of two 24-sample sinusoids of period 24 and period 4 with the two filters described above. Note the amplitude of the results. What can we conclude about this ``decomposition''?
  7. Load images ``al'' and ``ron''. Compute a 3-point horizontal weighted average of al using the kernel [ 0.25 0.5 0.25 ]. Compute a similar 3-point vertical average.
  8. Now convolve with both filters (sequentially). What equivalent single 2D convolution would produce the same result (give the convolution kernel, and show that the result is the same)?
  9. The result of this convolution may not look so different from the original, but try subtracting it from the original. What equivalent single 2D convolution would have produced this result?
  10. Take the result of the previous part (difference of original and average), and compute the following binary image:

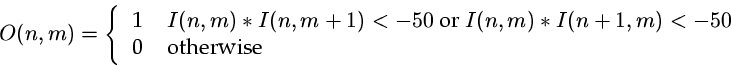
    \begin{displaymath} O(n,m) = \left\{ \begin{tabular} {ll} 1 & $I(n,m)*I(n,m+1) <... ...)*I(n+1,m) < -50$\space \\ 0 & otherwise \end{tabular}\right.\end{displaymath}

    Could we have computed it via a single convolution?
  11. Write a function mksine2 that constructs an array of samples from a 2D sine wave. This function should take similar arguments, but will require both xsize and ysize, and should also take an angular argument direction specifying the normal direction of the sine wave.

Mark Liberman
1/18/1999