In class on Tuesday 4/16, I briefly mentioned a recent piece of research claiming that in a population with any reasonable amount of contact, across a millenium or two, almost everyone winds up as almost everyone's ancestor. Specifically, the claim is that about 20% of the original population winds up with no descendents in the resulting population, but about 80% winds up as an ancestor to literally everyone in the resulting population.
My colleague Prof. Mann objected that this seems inconsistent with what is known about the geographical distribution of genetic mutations, namely that the clinal rates of occurrence tend to go to zero after a few hundred or thousand kilometers. I opined that the parts of this evidence dealing with MTDNA and Y chromosome DNA are not directly relevant, since these are inherited only in matrilineal and patrilineal sequences, and that the evidence from other DNA is not obviously inconsistent. This is a good example of scientific discussion in operation. The two of us are good friends and agree about almost everything, so you should think of this not as a sort of political debate, but rather as a discussion that helps both of us to clarify, interpret and judge new claims and results. Left on our own, we have this kind of discussion as a sort of internal dialogue -- but it's more interesting and usually more effective to have it with someone else!
The original paper that I was referring to is
Joseph T. Chang
"Recent Common Ancestors of all Present-Day Individuals." Advances in
Applied Probability, 31: 1002-1026, 1999.
Here is the abstract:
Previous study of the time to a common ancestor of all present-day individuals has focused on models in which each individual has just one parent in the previous generation. For example, ``mitochondrial Eve'' is the most recent common ancestor (MRCA) when ancestry is defined only through maternal lines. In the standard Wright-Fisher model with population size n, the expected number of generations to the MRCA is about 2n, and the standard deviation of this time is also of order n. This paper studies a two-parent analog of the Wright-Fisher model that defines ancestry using both parents. In this model, if the population size n is large, the number of generations, T_n, back to a MRCA has a distribution that is concentrated around lg n (where lg denotes base-2 logarithm), in the sense that the ratio T_n converges in probability to 1 as n goes to infinity. Also, continuing to trace back further into the past, at about 1.77 lg n generations before the present, all partial ancestry of the current population ends, in the following sense: with high probability for large n, in each generation at least 1.77 lg n generations before the present, all individuals who have any descendants among the present-day individuals are actually ancestors of all present-day individuals.
You can read the paper here, and find a proof of the result there (if you want to go through some non-trivial mathematics). You can also see Chang's reply to various discussants here.
It emerges from the discussion that biologists are used to working with one-parent models, for reasons that often make sense for reasoning about gene flow, but lead to answers about "most recent common ancestor" that do not correspond to the ordinary-language sense of "ancestor."
As Chang says in the discussion, "[t]he descendants of a common ancestor need not share any particular DNA from that ancestor, and it is even possible that none of the descendants has inherited any DNA from the ancestor. If you and I were investigating our common ancestry, we might conceive of an extreme case in which your mother's father is the same as my mother's father, but our common grandfather passed along no genes to either of us. Our ability to detect this common ancestor may be affected by these genetic circumstances, but the fact that we have a common grandfather would remain. I suspect a certain interest in our common ancestors comes naturally to most of us [...] I imagine if an anthropologist were somehow to divine or discover when and where our most recent common ancestors lived,the information would be valued."
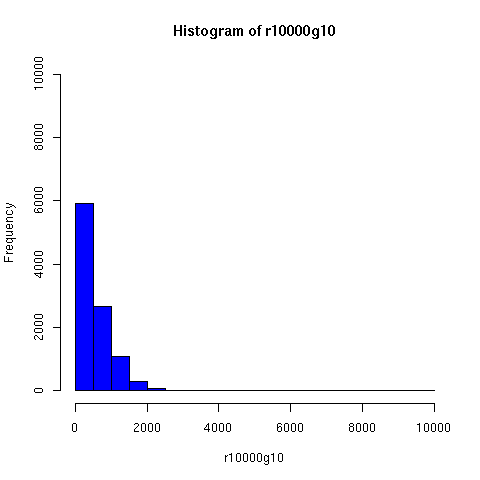
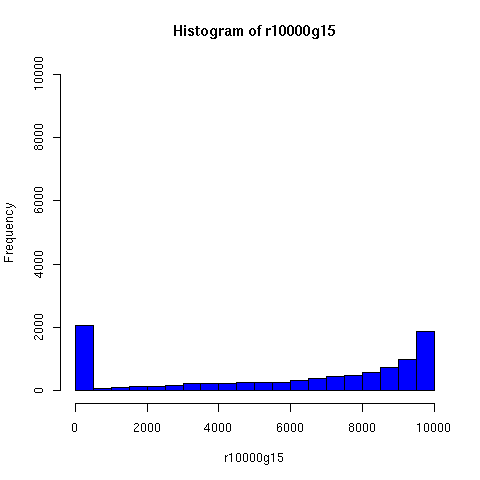
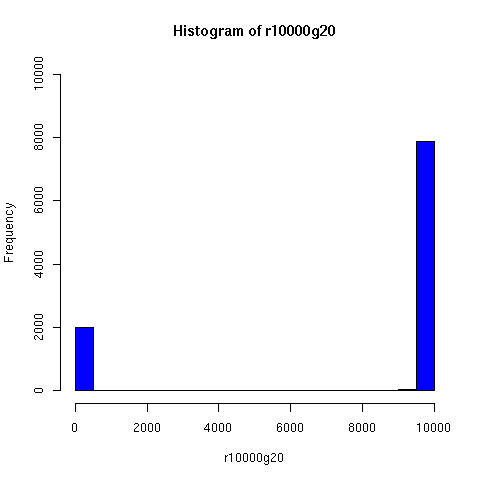
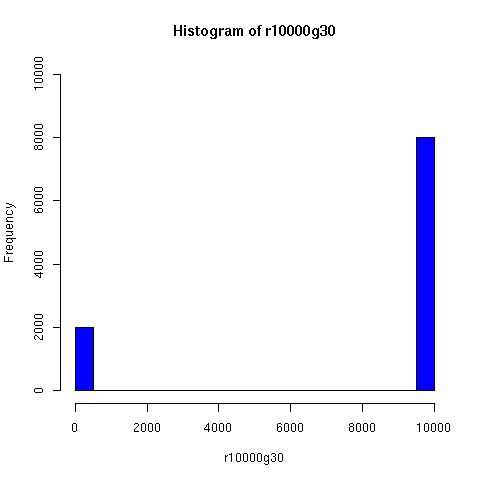
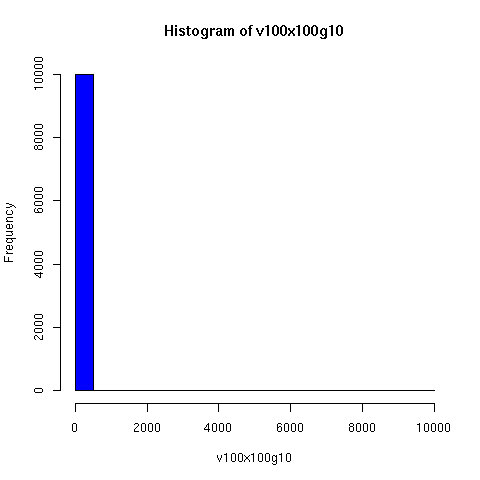
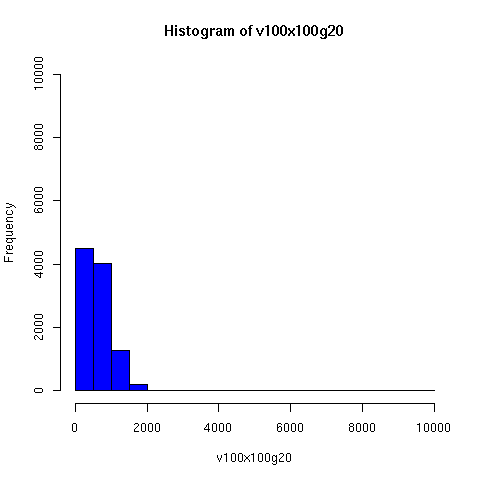
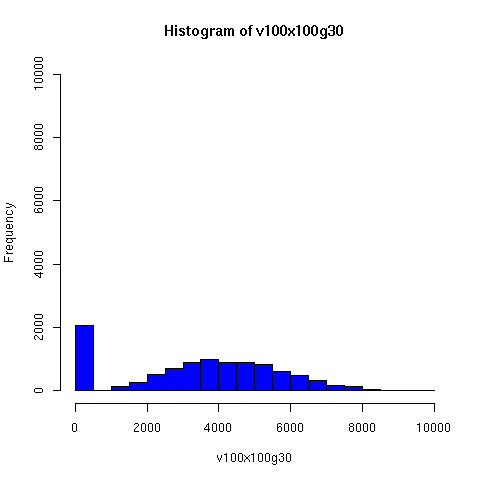
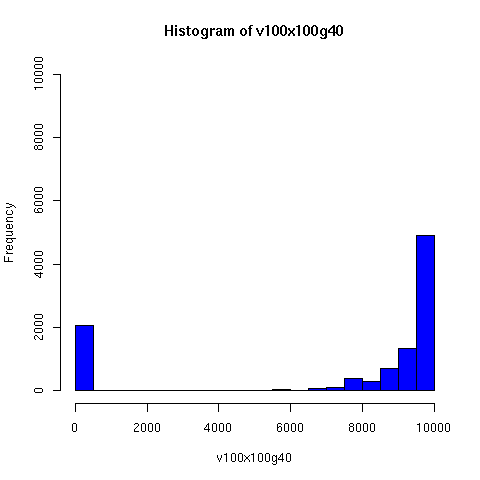
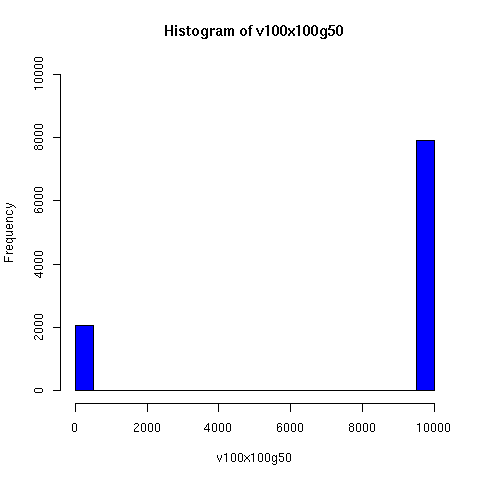
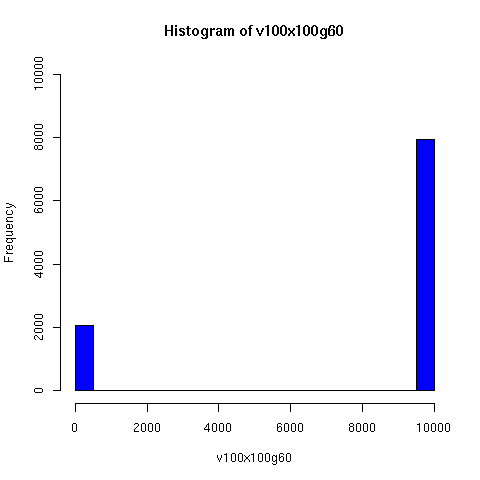
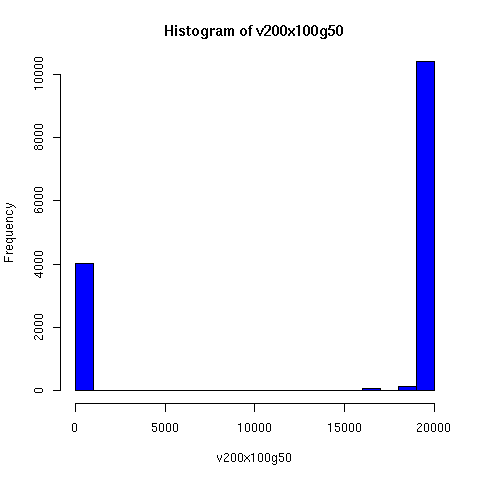
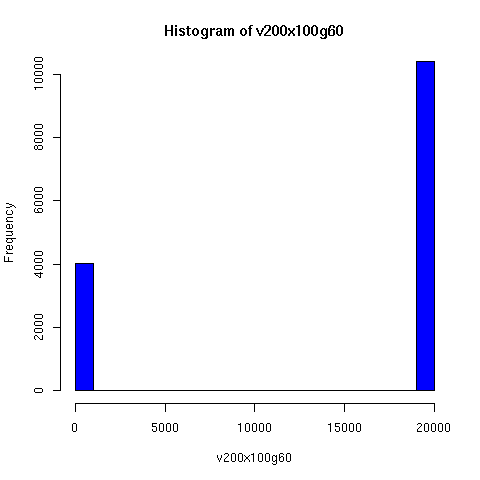
Starting from this paper, I looked a bit further into the theory and practice of descent networks, and ran some simulations. You can see the results of some of the simulations below.
I convinced myself that it really is true: under an amazingly wide range of assumptions, descent networks indeed do tend to a state in which about 20% of the original population has no descendents, while about 80% of the original population is ancestral to everyone. Furthermore, this can happen surprisingly rapidly -- within 100 generations (i.e. about 2000 years) in all the mating configurations I tried, and usually much faster. The effect of population size is just to increase the convergence time logarithmically, which is to say hardly at all.
Thus in the random-mating model, Chang's equation 1.77 ln(N) predicts that a population of 20 thousand people should converge to the 80/20 state in about 25 generations, while a population of 20 million people would take about 43 generations.
Severe "endogamy" (local mating) slows this down, but not by a large factor. For example, if people live in stable 100-person villages, and mate entirely within villages except for one exogamous mating per generation (i.e. 1 in 100), a population of 20,000 people still reaches the 80/20 state within about 50 generations (as you can see in the simulations below). I'd be surprised to learn that the true rate of exogamy was lower than this (or even this low). Of course, you can prevent this 80/20 effect from occuring by having completely isolated populations, but this does not seem very plausible for (say) Europe or Asia over the past couple of millennia. Using a random distribution of group sizes seems to make the convergence faster.
This is not an empirical claim, but rather a mathematical theorem that follows from the nature of descent graphs.
Even severe population bottlenecks will not prevent the 80/20 effect from applying. Thus if you start with a population of 100,000 individuals, reach the 80/20 equilibrium, and then at some point pass through a stage where only 2 are living before the population somehow increases again to 200,000, it's still true that each of the resulting 200,000 can trace ancestry back to 80% of the original 100,000 -- since each of the surviving 2 could.
For the same reason, one single "traveller" from group A, mating once with a member of a new group B, can (80% of the time) lead to descendent of the B group sharing the 80% of the ancestral members of A that (s)he brought along.
Both of these last points should help make it clear that this result says nothing about what proportion of DNA (if any) individuals inherit from their "universal ancestors". In fact, we can calculate how low this probability might be. Since the chance of inheriting a particular gene from a particular parent is 0.5, the per-gene chance of inheritance along a single chain of descent is 0.5^N after N generations. The probability that a given gene is NOT inherited down this chain is 1.0 - 0.5^N. If there are G genes whose chances of inheritance are independent, then the probability that no genes at all are inherited along such a single chain of descent is (1.0 - 0.5^N)^G. If the number of genes G is 30,000, then this probability (that no gene at all is inherited down a single chain of descent) is .4 after 15 generations, .8 after 17 generations, .97 after 20 generations, .999 after 25 generations, etc.
In a way, Chang's result just says that the relation "is an ancestor of" is way less selective than we normally think -- and therefore less interesting genetically -- once you go back a few tens of generations.
And so yes, there probably is a roughly 80% chance that a random European is
descended from Charlemagne, or that a random Middle Easterner is descended from
king Xerxes, or that a random Asian is descended from Genghis Khan. Of course,
the same could be said for the chances of peasants and slaves to be among our
ancestors. And even a fairly low rate of mating across regional boundaries is
probably enough to make it equally likely that a Spaniard is descended from
Xerxes, or that a Chinese is descended from Charlemagne.
The plots below come from a simple simulation that I wrote to test the idea. You can have a copy of the program if you're interested.

|

|

|

|
|
|
|
|
|
|
|
|