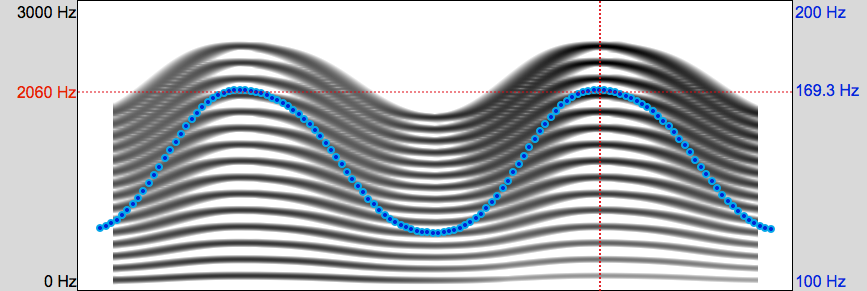
These 11 stimuli are the sum of 15 sine-wave overtones, with two peaks created by convolving a hamming window with a sawtooth whose baseline is always 120 Hz, and whose first peoak is always 169.34 Hz. The second peaks are at
[153.06 156.19 159.38 162.63 165.96 169.34 172.80 176.33 179.93 183.61 187.36]
Hz,
so that in stimulus #6 the two points are actually equal:

There are four spectral-balance conditions:
You can listen to results here:
| Parameters | Stimulus (A) | Stimulus (B) | Stimulus (C) | Stimulus (D) |
| 1: 169.34 120 153.06 | ||||
| 2: 169.34 120 156.19 | ||||
| 3: 169.34 120 159.38 | ||||
| 4: 169.34 120 162.63 | ||||
| 5: 169.34 120 165.96 | ||||
| 6: 169.34 120 169.34 | ||||
| 7: 169.34 120 172.80 | ||||
| 8: 169.34 120 176.33 | ||||
| 9: 169.34 120 179.93 | ||||
| 10: 169.34 120 183.61 | ||||
| 11: 169.34 120 187.36 |
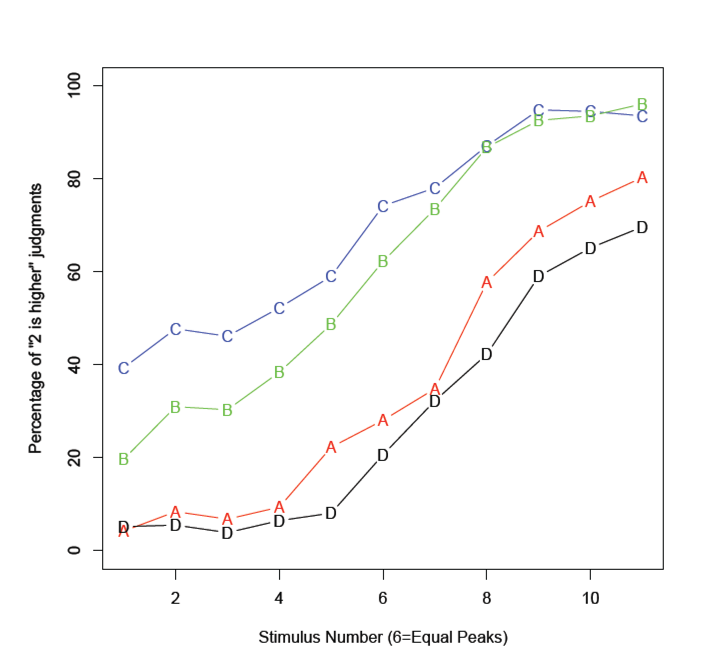
Prediction: If we do a forced-choice "Second peak is higher/lower" task, the identification function will be shifted in case (C) relative to case (A) (and maybe relative to case (B), I'm not sure), so that the peak with more high-frequency energy sounds higher.
Similarly, the case (D)( where the first peak has more high-frequency energy) should shift the ID function in the opposite direction.
Update: And it does! (Mean of ~50 subjects)
Except that the spectral quality of the second peak seems to have a really strong effect in and of itself -- perhaps listeners expect a sort of "final lowering" of spectral balance?
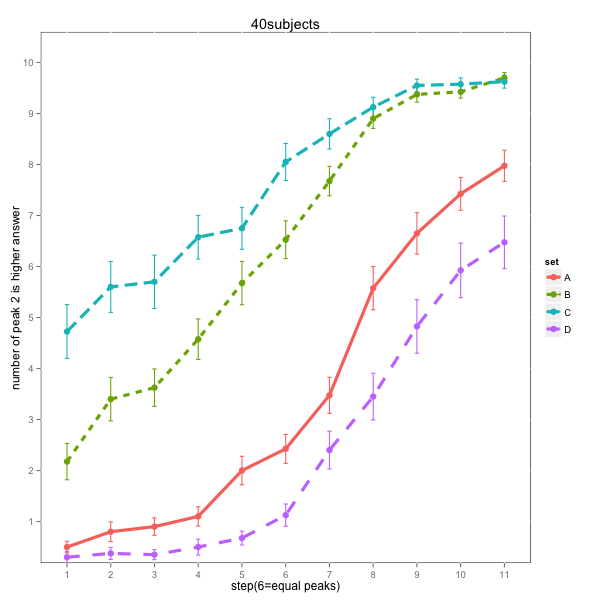
Post hoc analysis divided the subjects into 7 who attended exclusively to fundanmental frequency:
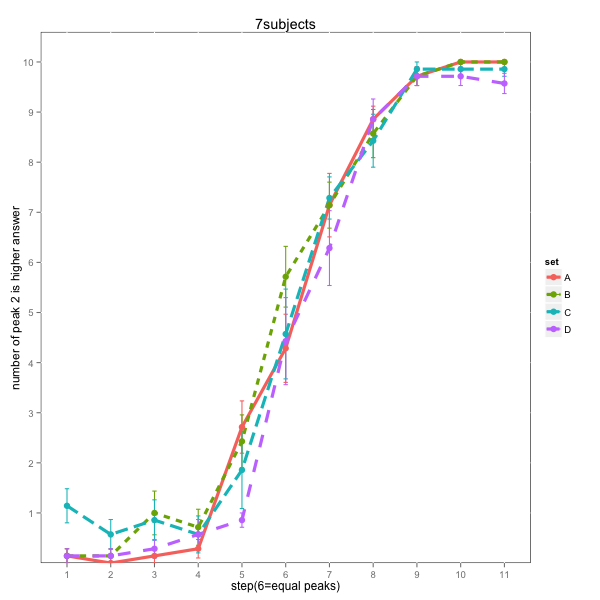
8 subjects who attended almost completely to timbre:
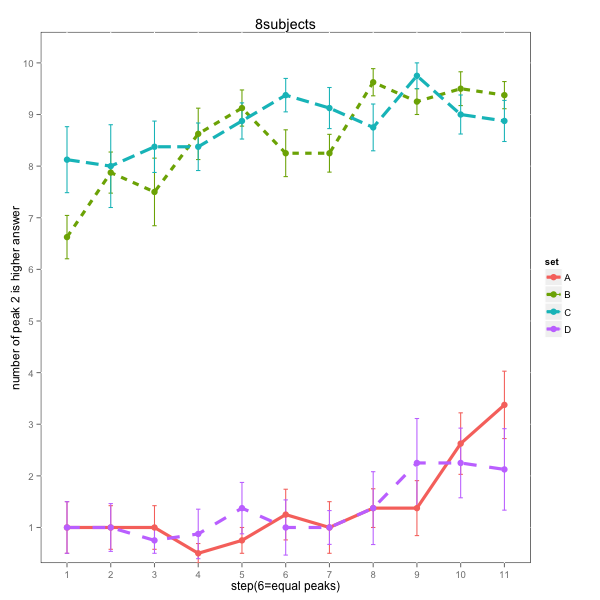
And 40 subjects whose responses were a mixture of both: